
第三讲俪数的极限
第三讲 函数的极限

函数的极限 一、 丞数极限的概念 二、 不同过程的数极限的关系 三、函数极限的性质
函数的极限 一、函数极限的概念 二、不同过程的函数极限的关系 三、函数极限的性质

函数的极限 拯数极限的概念 二、 不同过程的函数极限的关系 三、函数极限的性质
函数的极限 一、函数极限的概念 二、不同过程的函数极限的关系 三、函数极限的性质

一、函数极限的概念 (一) 自变量的不同变化过程 (二) 極数极限的统一定义 (三)各过程的函数极限定义 (四)举例
一、函数极限的概念 (一)自变量的不同变化过程 (二)函数极限的统一定义 (三)各过程的函数极限定义 (四)举例

函数极限的概念 (一) 自变量的不同变化过程 (二)函数极限的统一定义 (三)各过程的函数极限定义 (四)举例
一、函数极限的概念 (一)自变量的不同变化过程 (二)函数极限的统一定义 (三)各过程的函数极限定义 (四)举例

(一)自变量的不同变化过程 1.x>+00 2.x>-00 3.X>0 4.x>x0 5.x->x0 6.x→x0
(一)自变量的不同变化过程 x →+ x → − x → → − 0 x x → + 0 x x 0 x → x 1. 2. 3. 4. 5. 6.

(一)自变量的不同变化过程 1.x>+0 2.X> 3.X→0 4.x→x0 5.x→x0 6.x→x0
(一)自变量的不同变化过程 x →+ x → − x → → − 0 x x → + 0 x x 0 x → x 1. 2. 3. 4. 5. 6.
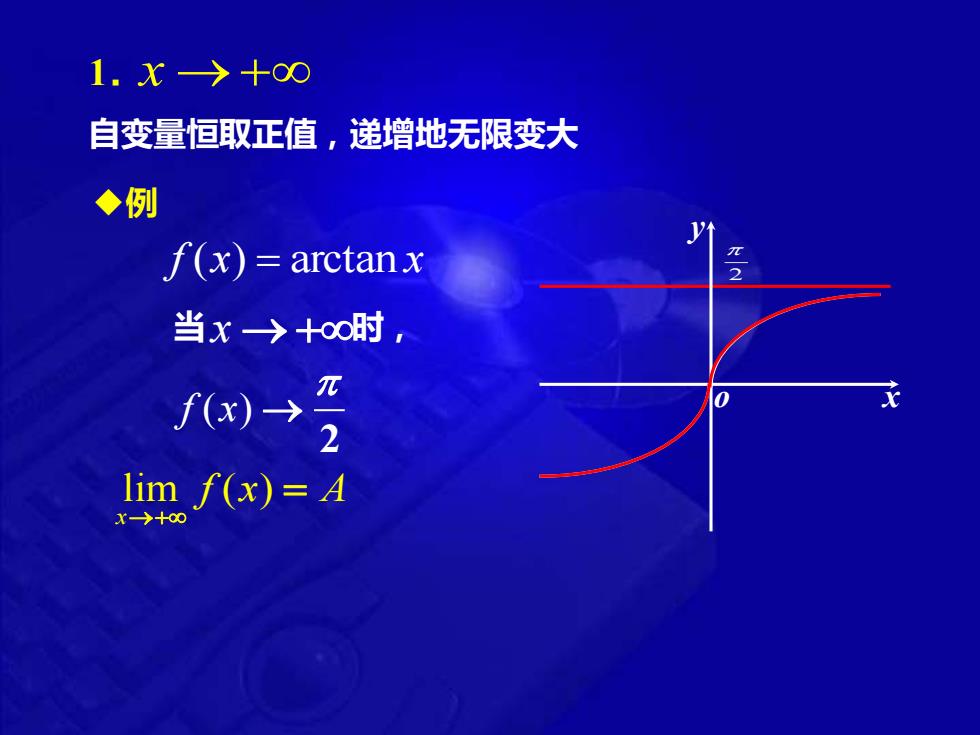
1.X>+00 自变量恒取正值,递增地无限变大 ◆例 f(x)=arctanx 2 当x>+oo时, f(x) 2 lim f(x)=A X→+0
1. 自变量恒取正值,递增地无限变大 x →+ ◆例 f (x) = arctan x 2 当 x → + 时, f x( ) → 2 o x y lim ( ) x f x A →+ =

(一)自变量的不同变化过程 1.x→+0 2.x→ 3.X→0 4.x今x0 5.x→x0 6.x>x0
(一)自变量的不同变化过程 x →+ x → − x → → − 0 x x → + 0 x x 0 x → x 1. 2. 3. 4. 5. 6.

(一)自变量的不同变化过程 1.x>+0 2.x→-0 3.X>00 4.x→x0 5.x→xd 6.x>x0
(一)自变量的不同变化过程 x →+ x → − x → → − 0 x x → + 0 x x 0 x → x 1. 2. 3. 4. 5. 6.