
第五讲 逯数的单调性与曲线的凹凸性
第五讲 函数的单调性与曲线的凹凸性

函数的单调性与曲线的凹凸性 函数的单调性 二、 曲线的凹凸性 三、小结
函数的单调性与曲线的凹凸性 一、函数的单调性 二、曲线的凹凸性 三、小结

函数的单调性与曲线的凹凸性 函数的单周性 二、 曲线的凹凸性 三、小结
函数的单调性与曲线的凹凸性 一、函数的单调性 二、曲线的凹凸性 三、小结

一、函数的单调性 (一)概念 (二) 判定 (三)应用
一、函数的单调性 (一)概念 (二)判定 (三)应用

函数的单调性 (一) 概念 (二) 判定 (三)应用
一、函数的单调性 (一)概念 (二)判定 (三)应用
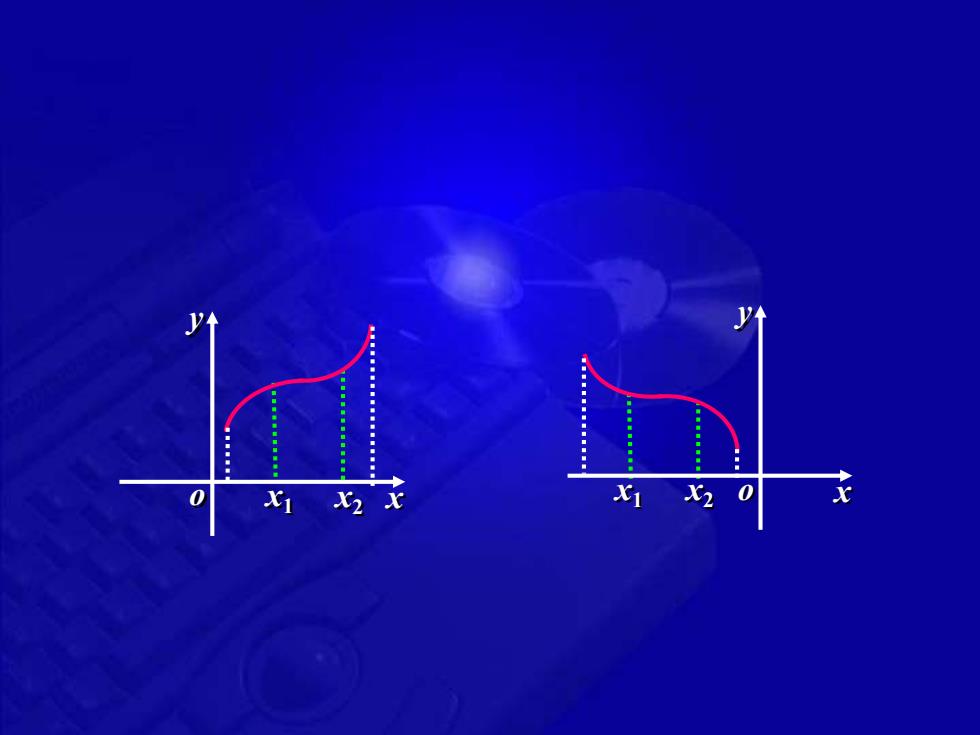
0 12x X2 0
x 1 x 2 o x x 1 x 2 y o x y

函数的单调性 () 概念 (二)判定 (三)应用
一、函数的单调性 (一)概念 (二)判定 (三)应用

一、函数的单调性 (一) 概念 (二) 判定 (三) 应用
一、函数的单调性 (一)概念 (二)判定 (三)应用
>判定定理 设函数y=f)在[a,上连续,在(a,b)内可导 (1)如果在(a,b)内f'x)≥0,且等号仅在有限多个点成立, 那么函数yfx)在a,b上单调增加; (2)如果在(a,b)内f'x)≤0,且等号仅在有限多个点成立, 那么函数y=fx)在a,b1上单调减少
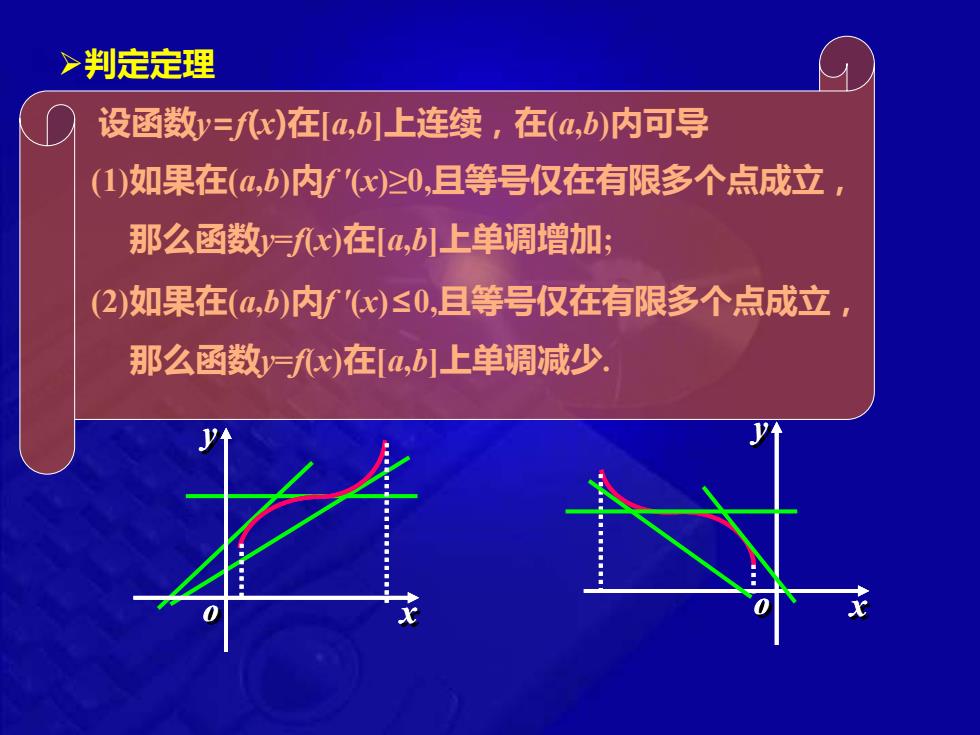
o x y ➢判定定理 设函数y=f(x)在[a,b]上连续,在(a,b)内可导 (1)如果在(a,b)内f '(x)≥0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调增加; (2)如果在(a,b)内f '(x)≤0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调减少. o x y

>判定定理 设函数y三f八x)在a,b1上连续,在(a,b)内可导 (1)如果在(a,b)内f'x)≥0,且等号仅在有限多个点成立, 那么函数y=fx)在4,b上单调增加; (2)如果在(a,b)内f'(x)≤0,且等号仅在有限多个点成立 那么函数y=x)在[a,上单调减少, ◆例1判定函数y=x-sin在[0,2x]上的单调性 ◆例2讨论函数y=ex-x-1的单调性 ◆例3讨论函数y=)x的单调性
➢判定定理 设函数y=f(x)在[a,b]上连续,在(a,b)内可导 (1)如果在(a,b)内f '(x)≥0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调增加; (2)如果在(a,b)内f '(x)≤0,且等号仅在有限多个点成立, 那么函数y=f(x)在[a,b]上单调减少. ◆例1 判定函数 y x x = − sin 在 0,2 上的单调性 ◆例2 讨论函数 1 x y e x = − − 的单调性 ◆例3 讨论函数 3 2 y x = 的单调性 o x y