
第四讲 微分中值定理习题课
第四讲 微分中值定理习题课

微分中值定理习题课 一、内容小结 二、题型练习
微分中值定理习题课 一、内容小结 二、题型练习

微分中值定理习题课 一、内容小结 二、题型练习
微分中值定理习题课 一、内容小结 二、题型练习

一、内容小结 (一) 中值定理 (二) 洛必达法则 (三)泰勒公式 (四)知识联系
一、内容小结 (一)中值定理 (二)洛必达法则 (三)泰勒公式 (四)知识联系

一、内容小结 (一) 中值定理 (二)洛必达法则 (三) 泰勒公式 (四)知识联系
一、内容小结 (一)中值定理 (二)洛必达法则 (三)泰勒公式 (四)知识联系

(1)在闭区间[a,b]上连续 fx) 件 (2)在开区间(4,b)内可导 满足 (3)a)=fb) 35∈(a,b 论 0 使得 =f'(5)(b-) 拉氏定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 f b f a ( ) ( ) − = f ( ) ( ) b a − 满足 条 件 结 论 (3) f(a)=f(b) 0

(1)在闭区间[4,b]上连续 fx) 件 满足 (2)在开区间(4,b)内可导 (3)fa)=fb) 35∈(a,b 论 使得 拉氏定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 满足 条 件 结 论 (3) f(a)=f(b)

(1)在闭区间[a,b]上连续 fx) 件 (2)在开区间(a,b)内可导 满足 (3)a)=fb) 35∈(a,b) 论 使得 5)=0 推广 罗尔定理 特 例 拉氏定理
罗尔定理 拉氏定理 推 广 特 例 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 满足 条 件 结 论 (3) f(a)=f(b) f ( ) 0 =
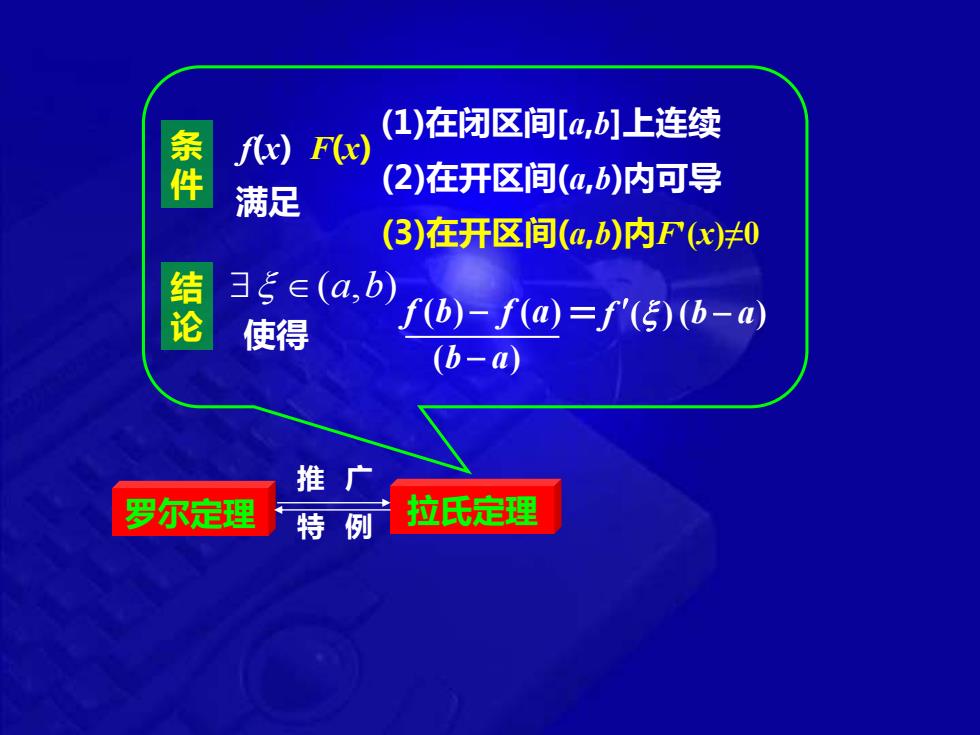
(1)在闭区间[a,b]上连续 f(x)F(x) 件 满足 (2)在开区间(a,b)内可导 (3)在开区间(a,b)内Fx)≠0 结 35∈(a,b) 使得 f(b)-f(a)=f'(5)(b-a) (b-a) 推广 罗尔定理 特 例 拉氏定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 f b f a ( ) ( ) − = f ( ) ( ) b a − 满足 条 件 结 论 罗尔定理 推 广 特 例 ( ) b a − F(x) (3)在开区间(a,b)内F'(x)≠0
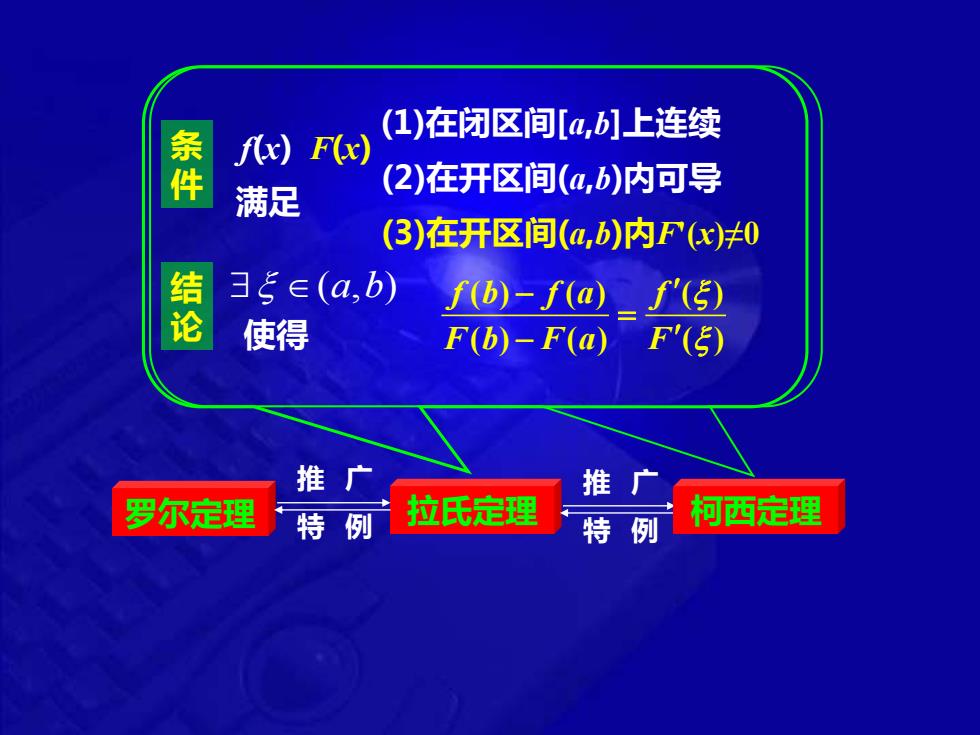
(1)在闭区间[a,b]上连续 fx)F(x) 件 (2)在开区间(a,b)内可导 满足 (3)在开区间(a,b)内Fx)≠0 35∈(a,b) f(b)-f(@)f(5) 论 使得 F(b)-F(a)F'(5) 推广 推 广 罗尔定理 特 例 拉氏定理 特 例 河西定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 ( ) ( ) ( ) ( ) ( ) ( ) f b f a f F b F a F − = − 满足 条 件 结 论 罗尔定理 推 广 特 例 F(x) (3)在开区间(a,b)内F'(x)≠0 推 广 特 例 柯西定理