
第一讲定积分的慨念与性质
第一讲 定积分的概念与性质

定积分的概念与性质 一、定积分的概念 二、定积分的性质
定积分的概念与性质 一、定积分的概念 二、定积分的性质

定积分的概念与性质 一、定积分的概念 二、定积分的性质
定积分的概念与性质 一、定积分的概念 二、定积分的性质
定积分的概念 (一)1例 (二) 定义 (三)可积条件 (四)几何意义
一、定积分的概念 (一)引例 (二)定义 (三)可积条件 (四)几何意义
一、定积分的概念 (一)1例 (二)定义 (三)可积条件 (四)几何意义
一、定积分的概念 (一)引例 (二)定义 (三)可积条件 (四)几何意义
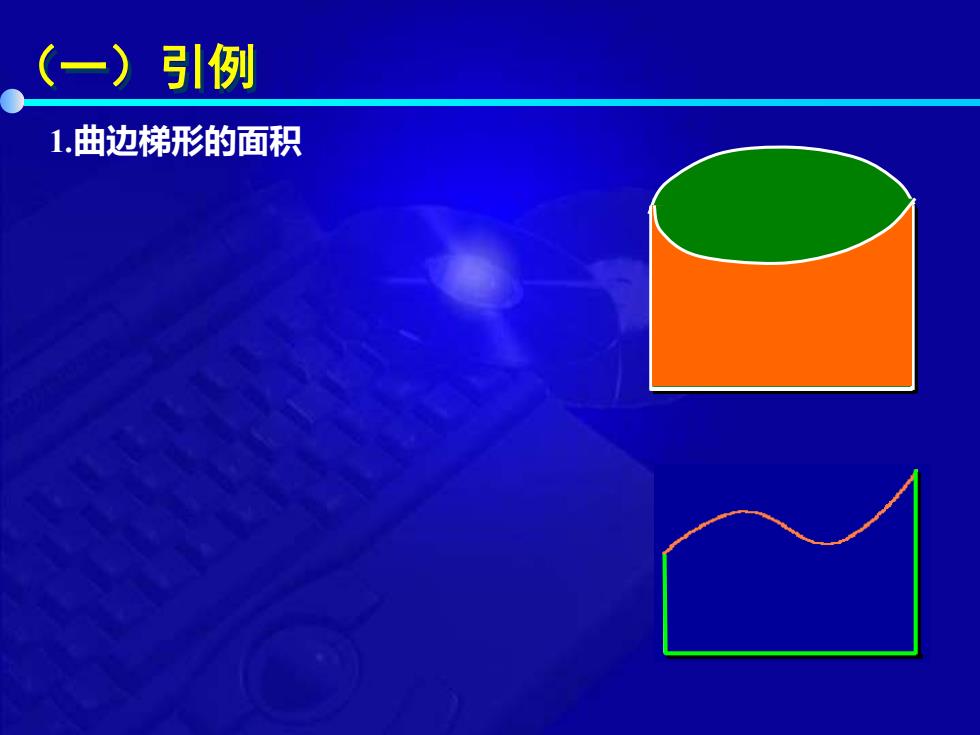
(一)引例 1.曲边梯形的面积
(一)引例 1.曲边梯形的面积
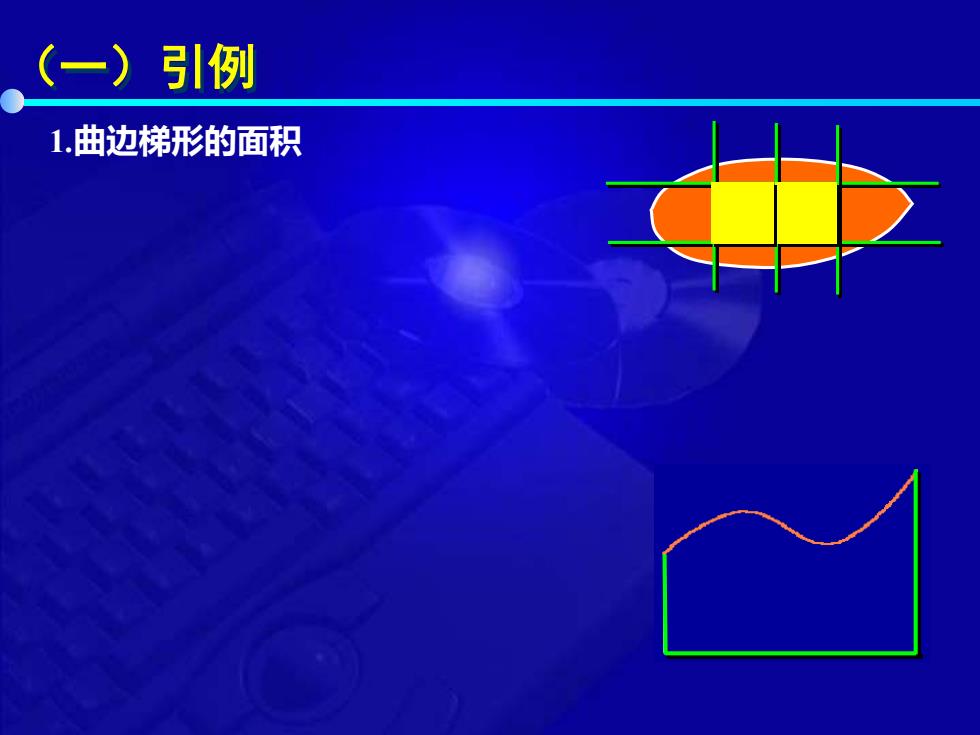
(一)引例 1.曲边梯形的面积
(一)引例 1.曲边梯形的面积
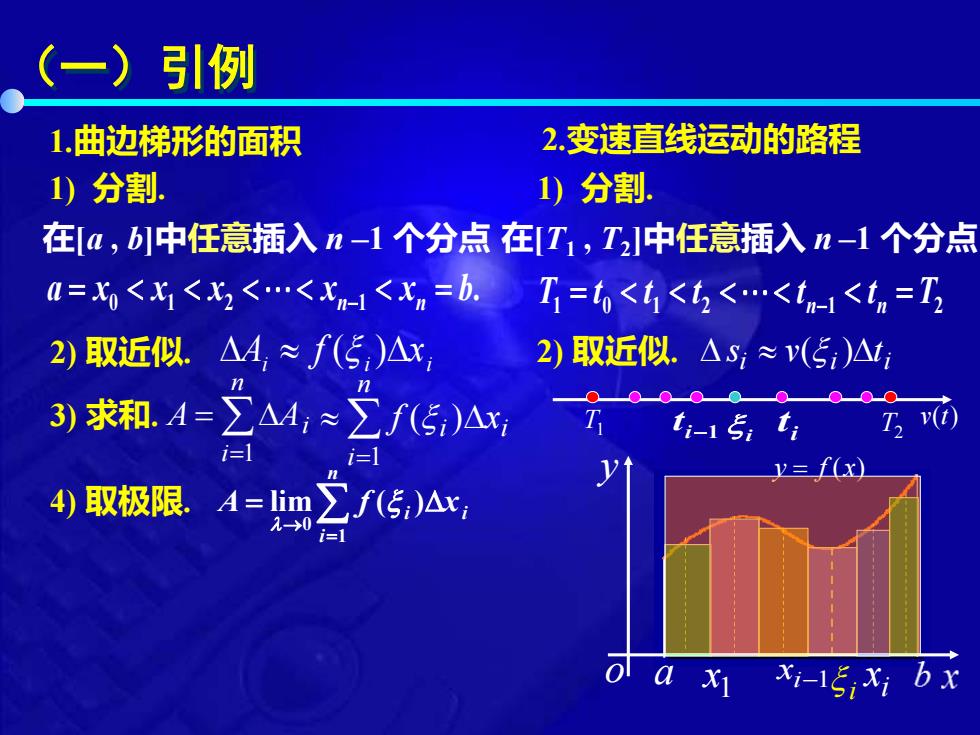
(一)引例 1.曲边梯形的面积 2.变速直线运动的路程 1)分割. 1)分割. 在a,b1中任意插入n-1个分点在IT1,T2]中任意插入n-1个分点 4=X<x<x<<XH<x=b.T=t<t<t<.<t<t=T 2)取近似.△4,≈f(5,)△x 2)取近似.△S,≈v(5)△t 3)求和.A=∑A4,≈∑f(5)△x i=l 三fx 4)取极限.A=1im∑f(传,)△x, i=l ol a x xi-1xi bx
(一)引例 a y o 1) 分割. 在[a , b]中任意插入 n –1 个分点 0 1 2 1 . n n a x x x x x b − = = 2) 取近似. ( ) A f x i i i 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 0 1 lim ( ) n i i i A f x → = = 1 x i xi−1 x i y = f (x) 1.曲边梯形的面积 2.变速直线运动的路程 1) 分割. T1 T2 v t( ) i 1 t − i t i i i i 2) 取近似. s v( )t 在[T1 , T2 ]中任意插入 n –1 个分点 T t t t t t T 1 0 1 2 1 2 n n − = =
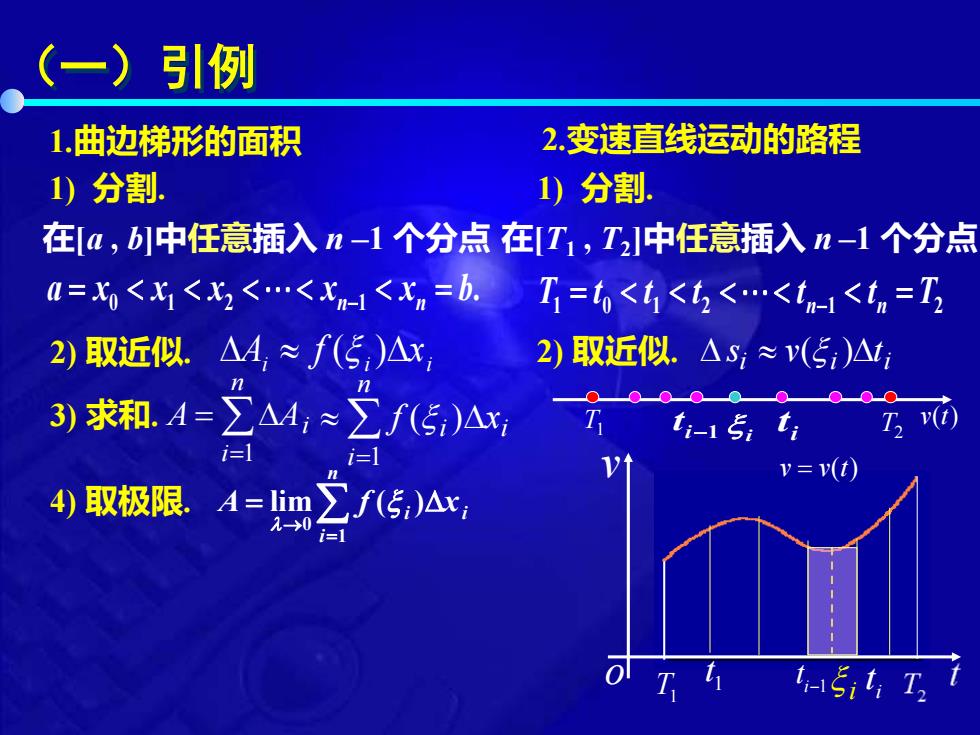
(一)引例 1.曲边梯形的面积 2.变速直线运动的路程 1)分割. 1)分割. 在a,b中任意插入n-1个分点在IT1,T中任意插入n-1个分点 4=X<X<x<<X<x=b.T=t<t<t<.<t<t=T 2)取近似.△4,≈f(5,)△x, 2)取近似.△S,≈v(5,)△ 3)求和.A=∑A4,≈∑f(5)△x i=l i=l v=(t) 4)取极限.A=1im∑f(5,)△x, →0 i=l tasit:T
(一)引例 T1 v o 1) 分割. 在[a , b]中任意插入 n –1 个分点 0 1 2 1 . n n a x x x x x b − = = 2) 取近似. ( ) A f x i i i 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 0 1 lim ( ) n i i i A f x → = = 1 t i i 1 t t − i v v t = ( ) 1.曲边梯形的面积 2.变速直线运动的路程 1) 分割. T1 T2 v t( ) i 1 t − i t i i i i 2) 取近似. s v( )t 在[T1 , T2 ]中任意插入 n –1 个分点 T t t t t t T 1 0 1 2 1 2 n n − = =

(一)引例 1.曲边梯形的面积 2,变速直线运动的路程 )分割, 1)分割 在[a,中任意插入n-1个分点在T1,T1中任意插入n-1个分点 何问题 <U=T 取近以 物理问题 )△t 3)求和.A= ∑A4≈∑f(5)Ax,3)求和. S≈∑(5)△ = 1= )取极限。 A=im∑f(5:)△x 4)取极限.s=1im∑v(传)△1 20 不同点:背景不同
(一)引例 1) 分割. 在[a , b]中任意插入 n –1 个分点 0 1 2 1 . n n a x x x x x b − = = 2) 取近似. ( ) A f x i i i 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 0 1 lim ( ) n i i i A f x → = = 1.曲边梯形的面积 2.变速直线运动的路程 1) 分割. i i i 2) 取近似. s v( )t 在[T1 , T2 ]中任意插入 n –1 个分点 T t t t t t T 1 0 1 2 1 2 n n − = = 3) 求和. 4) 取极限. 几 何 问 题 物 理 问 题 不同点:背景不同