
第一讲 导数概念
第一讲 导数概念

导数概念 一、导数概念 二、求导举例
导数概念 一、导数概念 二、求导举例

导数概念 一、导数概念 二、求导举例
导数概念 一、导数概念 二、求导举例

一、导数概念 (一)函数在一点处可导的概念 (二)函数在区间上可导的概念
一、导数概念 (一) 函数在一点处可导的概念 (二) 函数在区间上可导的概念

导数概念 (一)函数在一点处可导的概念 (二)函数在区间上可导的概念
一、导数概念 (一) 函数在一点处可导的概念 (二) 函数在区间上可导的概念

(一)函数在一点处可导的概念 1.1例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系
(一) 函数在一点处可导的概念 1.引例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系

(一)函数在一点处可导的概念 1.3引例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系
(一) 函数在一点处可导的概念 1.引例 2.导数定义 3.单侧导数 4.几何意义 5.可导与连续的关系
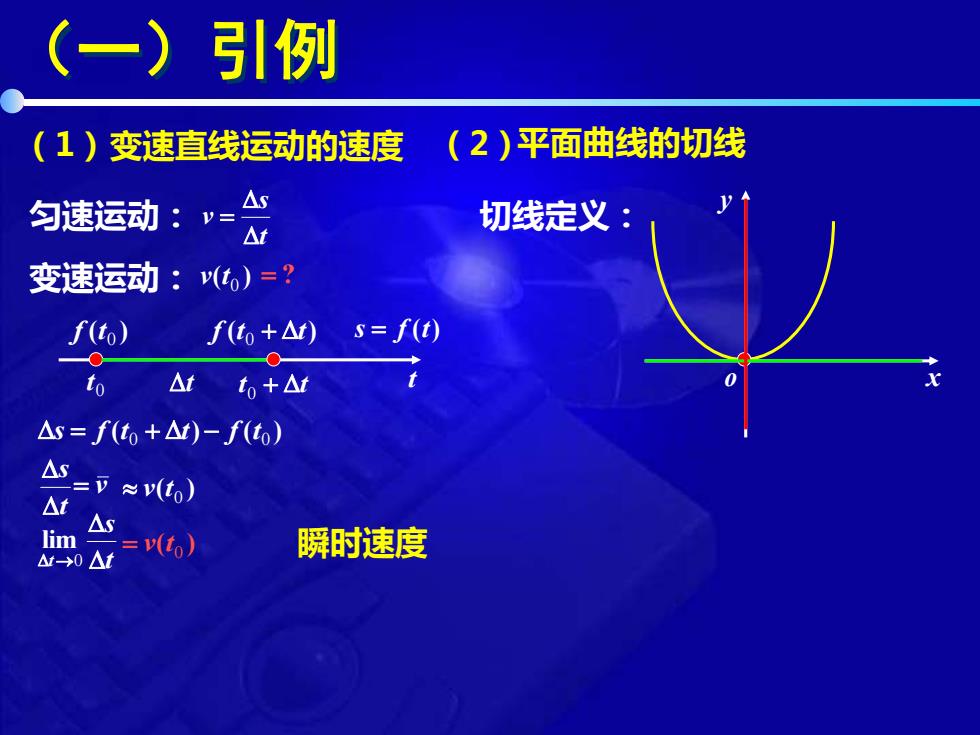
(一)引例 (1)变速直线运动的速度 (2)平面曲线的切线 匀速运动:v= 切线定义: △t 变速运动:()=? f(tò) f(t+△) s=f(t) 0 to △t to+△r △s=f(t+△r)-f(to) =v≈(to) t △S lim △→0△t =t6) 瞬时速度
x y o (一)引例 (1)变速直线运动的速度 匀速运动: 变速运动: (2)平面曲线的切线 t s v = t s = f (t) 0 t t t + t 0 ( ) 0 f t f (t + t) 0 ( ) ( ) 0 0 s = f t + t − f t t s = v ( ) 0 v t ( ) 0 v t = ? t s t →0 lim ( ) 0 = v t 瞬时速度 切线定义:

(一)引例 (1)变速直线运动的速度 (2)平面曲线的切线 匀速运动:v= 切线定义: △ 变速运动:v()=? f(to) f(to+△) s=f(t) M to △r to+△r 0 △s=f(i+△)-f(o) =v≈v(t) At △S lim M-0△t =v(t) 瞬时速度
(一)引例 (1)变速直线运动的速度 匀速运动: 变速运动: (2)平面曲线的切线 t s v = t s = f (t) 0 t t t + t 0 ( ) 0 f t f (t + t) 0 ( ) ( ) 0 0 s = f t + t − f t t s = v ( ) 0 v t ( ) 0 v t = ? t s t →0 lim ( ) 0 = v t 瞬时速度 切线定义: x y o M N

(一)引例 (1)变速直线运动的速度 (2)平面曲线的切线 匀速运动:v= 切线定义: △t 变速运动:()=? f(tò) f(t,+△) s=f(t) M 0 to △t to+△r △s=f(t+△r)-f(to) =v≈(to) t △s lim →0△t =t6) 瞬时速度
(一)引例 (1)变速直线运动的速度 匀速运动: 变速运动: (2)平面曲线的切线 t s v = t s = f (t) 0 t t t + t 0 ( ) 0 f t f (t + t) 0 ( ) ( ) 0 0 s = f t + t − f t t s = v ( ) 0 v t ( ) 0 v t = ? t s t →0 lim ( ) 0 = v t 瞬时速度 切线定义: x y o M N