
第九讲 曲率
第九讲 曲率

曲率 一、 弧微分 二、 曲率及其计算公式 三、曲率圆与曲率半径
曲 率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径

曲率 弧微分 二、 曲率及其计算公式 三、曲率圆与曲率半径
曲 率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径

>有向弧段的值 设函数fx)在(a,b)上具有连续导数 Mo(xo o) 一度量基点 Mx,y)一 曲线上任一点 M 规定: 0 ()曲线的正向与x增大的方向一致 (2)有向弧段MM的值为s 1s=M,☑M的方向与曲线的正向一致 →S>0 (M,的方向与曲线的正向相反 >S<0 s为x的函数,记为:S(x) s(x)为x的单调增加函数
M0 0 x M x x y 规定: o 设函数f(x)在(a,b)上具有连续导数 M0 (x0,y0 ) 度量基点 M(x,y) 曲线上任一点 (1) 曲线的正向与x增大的方向一致 s>0 s<0 s为x的函数,记为:s(x) s(x)为x的单调增加函数 ➢有向弧段的值 M0 M 的方向与曲线的正向相反 M0 M 的方向与曲线的正向一致 (2) 有向弧段 M M 的值为s 0 | s|=|M0 M|
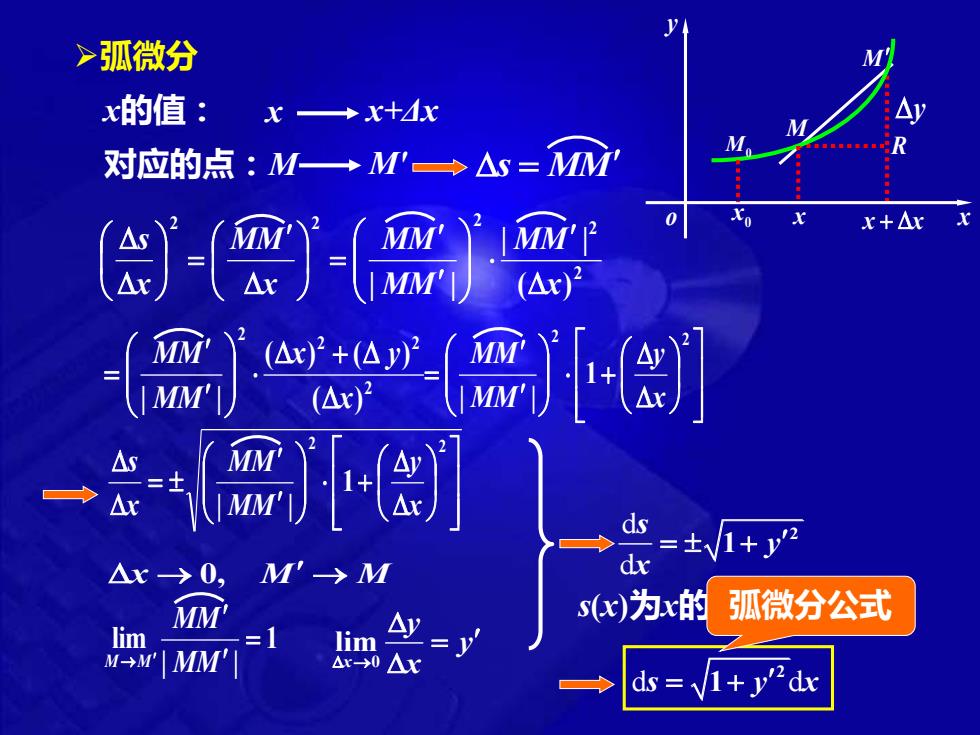
>弧微分 x的值:x→x+x 对应的点:M→M+△s=MM y-(两 x+△x jr恶 益跚町 =+y ds △x→0, M'-→M d MM' se)为x的 孤微分公式 lim =1] lim M→MMM' - △x→0△ ds v1+y"2dx
M R x + x M M0 0 x x x y o ➢弧微分 x的值: x x+Δx 对应的点:M M' → → x M M 0, 0 lim x y y → x = d d 2 1 s y x = + s(x)为x的单调增加函数 d d2 s y x = +1 弧微分公式 y s = MM 2 2 2 2 2 ( ) | | | | x MM MM MM x MM x s = = 2 2 2 2 ( ) ( ) ( ) | | x x y MM MM + = + = 2 2 1 | | x y MM MM + = 2 2 1 | | x y MM MM x s 1 | | lim = → MM MM M M

曲率 一、 弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径
曲 率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径

曲率 弧微分 二、 曲率乃其计算公式 三、曲率圆与曲率半径
曲 率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径

>背景描述曲线局部性质(弯曲程度) C2 △S M △S,N' △S 孤段弯曲程度越大转角越大 转角相同,弧段越短弯曲程度越大 >定义 M→M' MM'H△s 切线转角:△Cc △a MM的平均曲率 △S o△a+△a △ o K= lim da △S 曲线C在M处的曲率 △s→0 ds
描述曲线局部性质(弯曲程度) M1 M3 2 M2 S2 S1 M M S1 S2 N N 弧段弯曲程度越大转角越大 转角相同,弧段越短弯曲程度越大 1 ➢背景 ➢定义 + S S ) . M. M C M0 y o x s K s = →0 lim M M' 切线转角: K s = d ds = 曲线C在M处的曲率 | MM |=| s| MM 的平均曲率

△o lim d △s→0 △S ●注 (1)直线的曲率处处为零; (2)圆上各点处的曲率等于半径的倒数,半径越小曲率越大, >计算公式 'tana =y',a=arctan y', da=- 1+d,ds =+dx k= 1+y2 3/2 x=o(t) p(t)w"(t)-p"(t)w'(t) k= y=w(t) 3/2 9(0+w2() ◆例1抛物线=x2+bx+c上哪一点处的曲率最大?
➢计算公式 (1) 直线的曲率处处为零; (2) 圆上各点处的曲率等于半径的倒数,半径越小曲率越大. tan = y , 2 d d , 1 y x y = + = arctan , y 2 d 1 d s y x = + ⚫注 s K s = →0 lim d ds = ( ) 3 2 2 1 y k y = + ( ) ( ) x t y t = = C: ( ) 3 2 2 2 ( ) ( ) ( ) ( ) ( ) ( ) t t t t k t t − = + ◆例1抛物线y=ax2+bx+c上哪一点处的曲率最大?

曲率 一、 弧微分 二、 曲率及其计算公式 三、曲率圆与曲率半径
曲 率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径