
第一讲向量及其线性运算
第一讲 向量及其线性运算

第一讲向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影
第一讲 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影

第一讲向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影
第一讲 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影

>向量的概念 向量:既有大小,又有方向的量, 向量的表示:有向线段M1M2,或d,或a. M 向量的模:向量的大小,记作M,M2, 或a,或a >几种特殊的向量 自由向量:与起点无关的向量, 单位向量:模为1的向量 零向量:模为0的向量,记作0,或0 >注零向量的方向看作是任意的。 向径:起点为原点的向量
向量的表示: 向量的模 : 向量的大小, 向量: M1 M2 既有大小, 又有方向的量. 向径: 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 模为 1 的向量 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a , , 记作 M1M2 或 a , ➢向量的概念 ➢几种特殊的向量 ➢注 零向量的方向看作是任意的

>向量的关系 向量的相等:若向量π与万大小相等,方向相同, 则称a与五相等,记作a=万. 向量的平行:若向量a与五方向相同或相反, 则称a与万平行,记作a/万. 规定:零向量与任何向量平行. 负向量:与ā的模相同,但方向相反的向量称为ū的负向量, 记作-a 向量的共线:因平行向量可平移到同一直线上,故两向量平行 又称两向量共线. 向量的共面:若k(仑3)个向量经平移可移到同一平面上, 则称此k个向量共面
规定: 零向量与任何向量平行 . 因平行向量可平移到同一直线上, 故两向量平行 又称两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . ➢向量的关系 向量的相等 : 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a=b . 向量的平行 : 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, 记作 a∥b . 负向量 : 与a 的模相同, 但方向相反的向量称为 a 的负向量, 记作-a . 向量的共线 : 向量的共面 :

第一讲向量及其线性运算 向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影
第一讲 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影

第一讲向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影
第一讲 向量及其线性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、向量线性运算的坐标表示式 五、向量的模、方向角和投影

二、向量的线性运算 1.向量的加法 2.向量的减法 3.向量与数的乘法
二、向量的线性运算 1.向量的加法 2.向量的减法 3.向量与数的乘法

二、向量的线性运算 1,向量的加法 2.向量的减法 3.向量与数的乘法
二、向量的线性运算 1.向量的加法 2.向量的减法 3.向量与数的乘法
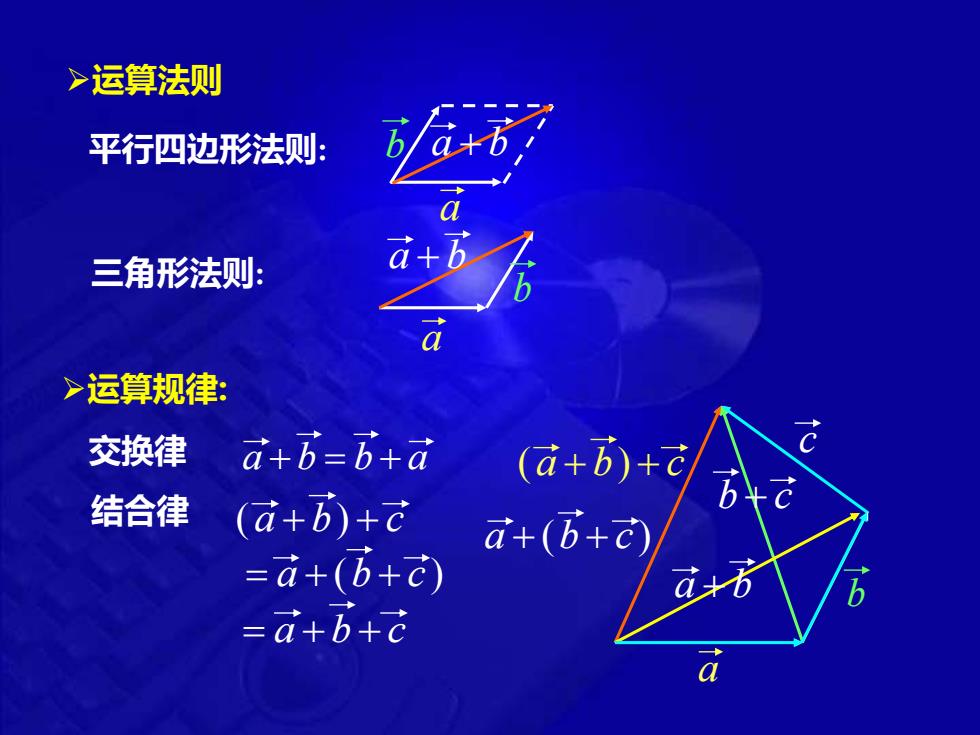
>运算法则 平行四边形法则: 三角形法则: >运算规律: 交换律 a+b-b+a (a+B)+c 结合律 (a+B)+c a+(B+c) =a+(b+ -a+b+c
三角形法则: 平行四边形法则: ➢运算规律: 交换律 结合律 b b a + b = b + a (a + b) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) (a + b) + c a a a + b a + b ➢运算法则