《高等数学》课程教学资源（PPT课件）第十章 重积分_第一节 二重积分的定义与性质_二重积分的定义与性质

第一讲二重积分的概念与性质

第一讲 二重积分的概念与性质

二重积分的概念与性质 一、二重积分的概念 二、二重积分的性质

二重积分的概念与性质 一、二重积分的概念 二、二重积分的性质

二重积分的概念与性质 一、二重积分的概念 二、二重积分的性质

二重积分的概念与性质 一、二重积分的概念 二、二重积分的性质

一、二重积分的概念 (一)引例 (二)定义

一、二重积分的概念 （一）引例 （二）定义

二重积分的概念 (一) 引1例 (二) 定义

一、二重积分的概念 （一）引例 （二）定义

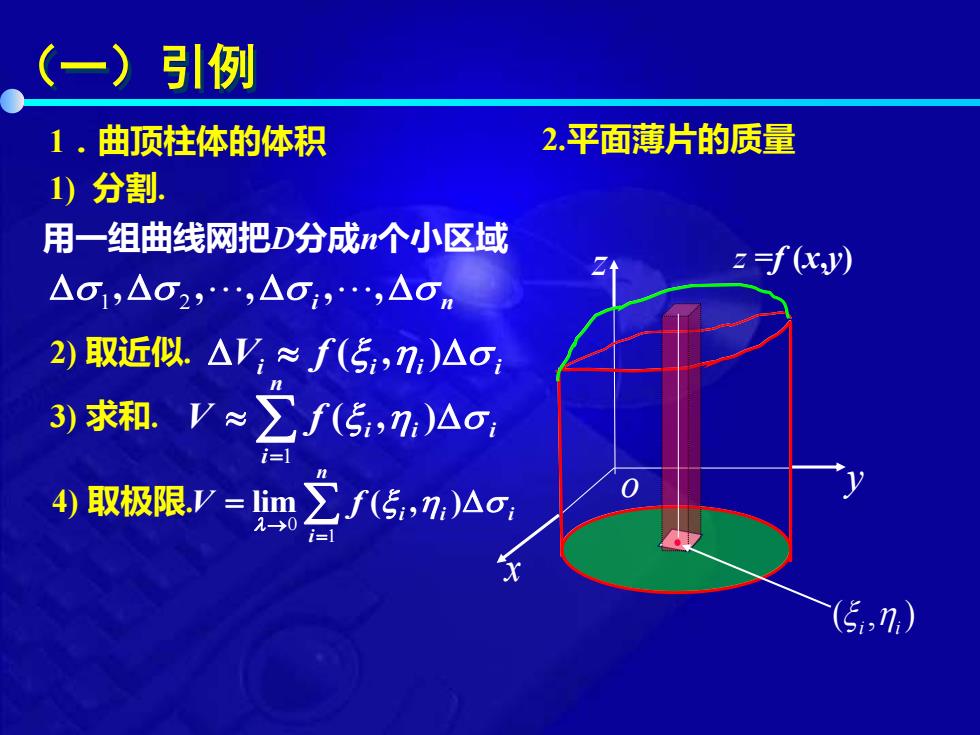
(一)引例 1.曲顶柱体的体积 2.平面薄片的质量 1)分割. 用一组曲线网把D分成个小区域 2f(y) △O1,△O2,△O,.,△0m 2)取近似.△V≈f(5,7,)△o, 3)求和.V≈∑f(5,)Ao i=] 4取极限y=1im∑f(5,n,)△c, -0 (5,7,）

（一）引例 1．曲顶柱体的体积 x z o y z =f (x,y) 1) 分割. 用一组曲线网把D分成n个小区域 2) 取近似. 3) 求和. 4) 取极限.    i  n , ,  , ,  , 1 2 • ( , ) i i  i i i i V  f ( , ) =   n i i i i V f 1 ( , )  = → =  n i i i i V f 1 0     lim ( , ) 2.平面薄片的质量

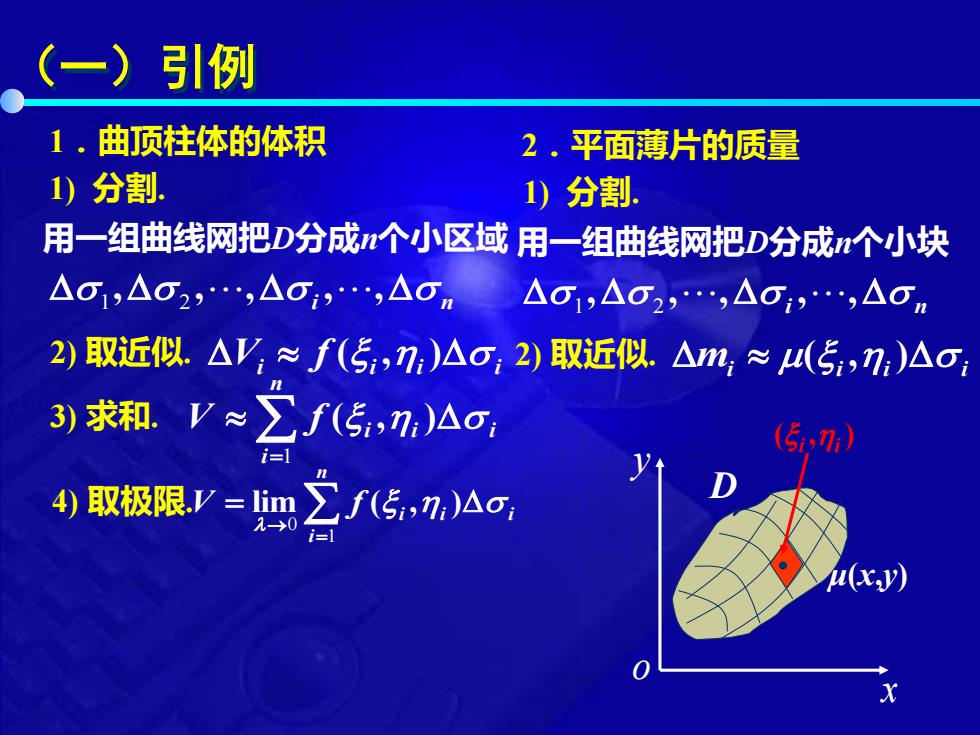
(一)引例 1.曲顶柱体的体积 2.平面薄片的质量 1)分割. 1)分割. 用一组曲线网把D分成个小区域用一组曲线网把D分成n个小块 △C1,△C2,AO,△on△o1,△o2,△o1,△o 2)取近似△V≈f(5,7:)△o,2)取近似.△m,≈4(5,7)△o 3)求和.V≈∑f(5,n)△o, (5,7 i=1 4)取极限.V=1im∑f(5,7,)△o 20 i=l u(x.y)

（一）引例 1．曲顶柱体的体积 1) 分割. 用一组曲线网把D分成n个小区域 2) 取近似. 3) 求和. 4) 取极限.    i  n , ,  , ,  , 1 2 i i i i V  f ( , ) =   n i i i i V f 1 ( , )  = → =  n i i i i V f 1 0     lim ( , ) 2．平面薄片的质量 D ( , ) i i  x y o μ(x,y) 1) 分割. 用一组曲线网把D分成n个小块    i  n , ,  , ,  , 1 2 2) 取近似. mi    i i  i ( , )

(一)引例 1.曲顶柱体的体积 2.平面薄片的质量 1)分割 1)分割 用一组曲线网把D分成个小区域用一组曲线网把D分成个小块 何问题A △1 物理问题 2) ）△2)取 3)求和.V≈∑f(5,n)△o3)求和.m≈∑4(5,7)△o = 4)取极限.V=im∑f(传，n,)△c4)取极限.m=1im∑4(5,7，)△o 2→0 2→0 不同点：背景不同

（一）引例 1．曲顶柱体的体积 1) 分割. 用一组曲线网把D分成n个小区域 2) 取近似. 3) 求和. 4) 取极限.    i  n , ,  , ,  , 1 2 i i i i V  f ( , ) =   n i i i i V f 1 ( , )  = → =  n i i i i V f 1 0     lim ( , ) 2．平面薄片的质量 1) 分割. 用一组曲线网把D分成n个小块    i  n , ,  , ,  , 1 2 2) 取近似. mi    i i  i ( , ) 3) 求和. =   n i m i i i 1 ( , )  4) 取极限. = → =  n i m i i i 1 0      lim ( , ) 不同点：背景不同 几 何 问 题 物 理 问 题

(一)引例 1.曲顶柱体的体积 2.平面薄片的质量 1)分割. 分割1)分割. 用一组曲线网把D分成个小区域用一组曲线网把D分成个小块 △O1,△g2,△C,△On△o,△o2,△o1,.,△g 取近似△Y≈f(5,羽近似2)取近似△m,≈4(5,7，)△o 2)1 3)求和. ∑f(5,n求和3)求和.m≈ ∑4(5,7，)△σ， i=l i=l 4) 取极限.y=im f(5取极限)取极限.m=im∑4（传，7）Ao 20 %→0 不同点：背景不同 相同点：方法相同

（一）引例 1．曲顶柱体的体积 1) 分割. 用一组曲线网把D分成n个小区域 2) 取近似. 3) 求和. 4) 取极限.    i  n , ,  , ,  , 1 2 i i i i V  f ( , ) =   n i i i i V f 1 ( , )  = → =  n i i i i V f 1 0     lim ( , ) 2．平面薄片的质量 1) 分割. 用一组曲线网把D分成n个小块    i  n , ,  , ,  , 1 2 2) 取近似. mi    i i  i ( , ) 3) 求和. =   n i m i i i 1 ( , )  4) 取极限. = → =  n i m i i i 1 0      lim ( , ) 不同点：背景不同 相同点：方法相同 分 割 取近似 求 和 取极限

(一)引例 1.曲顶柱体的体积 2.平面薄片的质量 1)分割. 1)分割. 用一组曲线网把D分成个小区域用一组曲线网把D分成个小块 △O1,△02，△o,△On△o1,△O2,△o1,.,△o 2)取近似.△Y≈f(5,:)△O,2)取近似.△m,≈(5,7，)△O 3)求和.V≈∑f(5,n,)△o:3)求和.m≈∑45,7，)△o, 4)取极限.y=im】 2→0 ∑f(5,n.)△g4)取极限m=四∑4(5，n:)△0 20 不同点：背景不同 相同点：方法相同数学形式相同 ∑/G7aa

（一）引例 1．曲顶柱体的体积 1) 分割. 用一组曲线网把D分成n个小区域 2) 取近似. 3) 求和. 4) 取极限.    i  n , ,  , ,  , 1 2 i i i i V  f ( , ) =   n i i i i V f 1 ( , )  = → =  n i i i i V f 1 0     lim ( , ) 2．平面薄片的质量 1) 分割. 用一组曲线网把D分成n个小块    i  n , ,  , ,  , 1 2 2) 取近似. mi    i i  i ( , ) 3) 求和. =   n i m i i i 1 ( , )  4) 取极限. = → =  n i m i i i 1 0      lim ( , ) 不同点：背景不同 相同点：方法相同 数学形式相同 = →  n i i i i f 1 0     lim ( , )