
第大讲对坐标的曲面积分
第六讲 对坐标的曲面积分

对坐标的曲面积分 一、对坐标的曲面积分的概念 二、对坐标的曲面积分的性质 三、对坐标的曲面积分的计算 四、两类曲面积分之间的联系
对坐标的曲面积分 一、对坐标的曲面积分的概念 二、对坐标的曲面积分的性质 三、对坐标的曲面积分的计算 四、两类曲面积分之间的联系

对坐标的曲面积分 对坐标的曲面积分的概念 二、对坐标的曲面积分的性质 三、对坐标的曲面积分的计算 四、两类曲面积分之间的联系
对坐标的曲面积分 一、对坐标的曲面积分的概念 二、对坐标的曲面积分的性质 三、对坐标的曲面积分的计算 四、两类曲面积分之间的联系

一、对坐标的曲面积分的概念 (一)预备知识 (二) 1例 (三)对坐标的曲面积分的定义
一、 对坐标的曲面积分的概念 (一)预备知识 (二)引例 (三)对坐标的曲面积分的定义

对坐标的曲面积分的概念 (一) 预备知识 (二)1例 (三)对坐标的曲面积分的定义
一、 对坐标的曲面积分的概念 (一)预备知识 (二)引例 (三)对坐标的曲面积分的定义

>曲面的侧 通过曲面上任一点处法向量的指向来指定 例:Σ:z=(x,y) n=-3,0cos7>0上侧 (3x,z,-1)c0sy0右侧 (y,-1,y)cosB<0左侧 有向曲面规定了侧的曲面
➢曲面的侧 通过曲面上任一点处法向量的指向来指定 例: = : ( , ) z z x y n = ( , ,1) x y − − z z cos 0 上侧 ( , , 1) x y z z − cos 0 下侧 = : ( , ) x x y z n = (1, , ) y z − − x x cos 0 前侧 ( 1, , ) y z − x x cos 0 后侧 = : ( , ) y y x z n = ( ,1, ) x z − − y y cos 0 右侧 ( , 1, ) x z y y − cos 0 左侧 o x y z o x y z o x y z ➢有向曲面 规定了侧的曲面

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为旷 单位时间内流向区域指定侧的流量Φ=? (位,)<
➢流向平面一侧的流量 设有一面积为A的平面闭区域 单位时间内流向区域指定侧的流量 = ? ( , ) 2 v n 流体流速为v

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为时 单位时间内流向区域指定侧的流量Φ=A位,方 心,m<2 V=A cos(,)=Ai
➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量 = Av n ( , ) 2 v n V A v v n Av n = = | | cos( , ) v n

>流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为下 单位时间内流向区域指定侧的流量Φ=A位, 低用=子V=0=4pjo反万
➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量 = Av n ( , ) 2 v n = V A v v n Av n = = = 0 | | cos( , ) v n
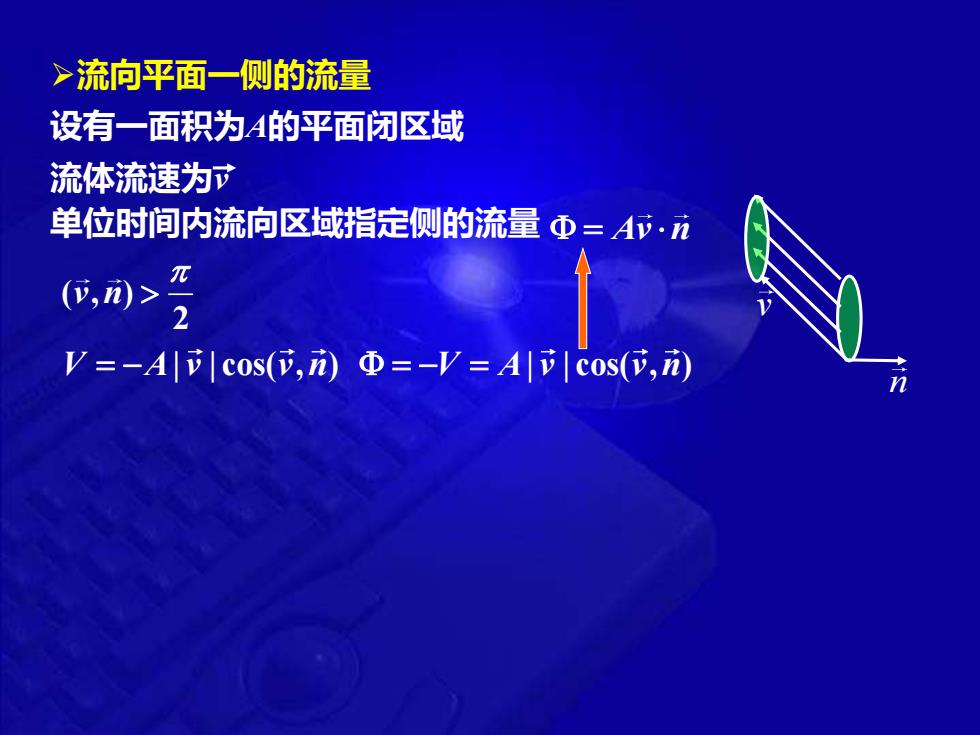
>流向平面一侧的流量 设有一面积为4的平面闭区域 流体流速为 单位时间内流向区域指定侧的流量Φ=A)· (,m>2 V=-A||c0s(位,)Φ=-V=A|币|c0s(正,)
➢流向平面一侧的流量 设有一面积为A的平面闭区域 流体流速为v 单位时间内流向区域指定侧的流量 = Av n ( , ) 2 v n V A v v n = − | | cos( , ) v n = − = V A v v n | | cos( , )