《高等数学》课程教学资源（PPT课件）第十一章 曲线积分与曲面积分_第八节 曲面积分习题课_曲面积分习题课

第八讲曲面积分习题课

第八讲 曲面积分习题课

曲面积分习题课 一、内容小结 二、题型练习

曲面积分习题课 一 、内容小结 二 、题型练习

曲面积分习题课 一、 内容小结 二、题型练习

曲面积分习题课 一 、内容小结 二 、题型练习

对面积的曲面积分 对坐标的曲面积分 曲面壳的质量：八pP(x,y)ds流量：∬Pdvd+dzdc+Rdxd >定义-m2八%5儿a =四∑R5n,5As,) 线性 可加性 >性质物理意义∬dS=S 与侧有关判Rdd=-刂Rdd: >计算 直接计算 一投、二代、三换（选择） 一投、二代、三定号（确定） 高斯公式 转化 >联系 ∬(Psa+csB+Reos7）as=∬Pwd+Oddr+Rdd

对面积的曲面积分 ➢定义 ➢联系 对坐标的曲面积分 曲面壳的质量: ( , , )d x y z S  流量: P y z Q z x R x y d d d d d d  + +  0 1 ( , , )d lim ( , , ) n i i i i i f x y z S f S     →  =  =   0 1 d d lim ( , , )( ) n i i i i xy i R x y R S      → = =    ➢性质 线性 可加性 物理意义 dS S  =  与侧有关 R x y R x y d d d d   = −   ➢计算 直接计算 一投、二代、三换(选择) 一投、二代、三定号(确定) 高斯公式 转化 ( P Q R P y z Q z x R x y cos cos cos dS d d + d d + d d    )   + + =  

曲面积分习题课 一、 内容小结 二、题型练习

曲面积分习题课 一 、内容小结 二 、题型练习

曲面积分习题课 一、内容小结 二、 题型练习

曲面积分习题课 一 、内容小结 二 、题型练习

二 题型练习 (一) 对面积的曲面积分的计算 (二)对坐标的曲面积分的计算

二 题型练习 (一) 对面积的曲面积分的计算 (二) 对坐标的曲面积分的计算

二题型练习 一) 对面积的曲面积分的计算 (二) 对坐标的曲面积分的计算

二 题型练习 (一) 对面积的曲面积分的计算 (二) 对坐标的曲面积分的计算

>计算公式 (1)2:=(,(c,)eD ∬fx,as=∬fx(x,yW++d D (2)2:y=Jy(c,c,)eD ∬f,3)as=∬fx,x,z,zW1++dd (3)∑：x=x0,z0eD ∬x,eas=∬/xU,W++dt业

➢计算公式 (3) (2) (1) 2 2 ( , , )d ( , , ( , )) d d 1 xy x y D f x y z S f x y z x y z z x y  = + +   Σ： ( , ),( , ) x y z z x y x y D =  Σ： ( , ) ,( , ) x z y y x z x z D =  2 2 ( , , )d ( , ( , ), ) 1 d dz xz x z D f x y z S f x y x z z y y x  = + +   Σ： ( , ),( , ) y z x x y z y z D =  2 2 ( , , )d ( ( , ), , ) d d 1 yz y z D f x y z S f x y z y z x x y z  = + +  

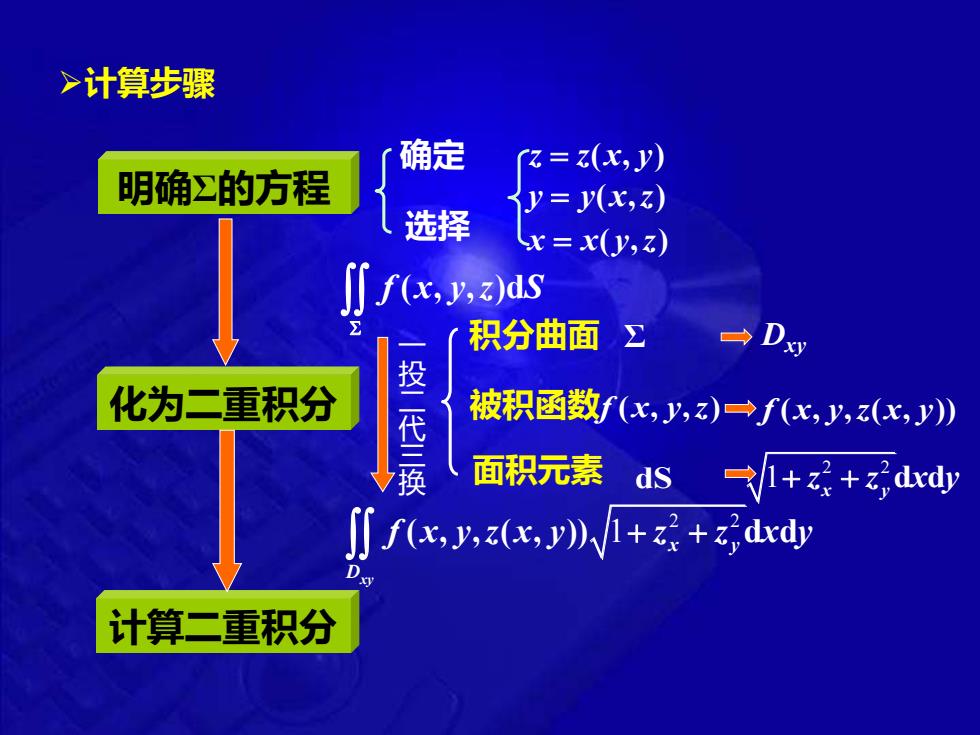
>计算步骤 确定 3=(比，) 明确Σ的方程 y=y(x,z) 选择 x=x(y,z) ∬fx,Jz)as Σ 积分曲面Σ →Dy 化为二重积分 投代换 被积函数f(x,y,z)→f(x,y,(c,y) 面积元素 ds一1+z+zdrd ∬fx,J,z(,y以W1++dd 计算二重积分

➢计算步骤 明确Σ的方程 化为二重积分 确定 选择 y y x z = ( , ) x x y z = ( , ) f x y z S ( , , )d   一 投 二 代 三 换 f x y z ( , , ) 积分曲面 Σ 被积函数 f x y z x y ( , , ( , )) 面积元素 dS Dxy 2 2 1+ + z z x y x y d d 2 2 ( , , ( , )) d d 1 xy x y D f x y z x y z z x y + +  计算二重积分 z z x y = ( , )