
第五讲对面积的曲面积分
第五讲 对面积的曲面积分

对面积的曲面积分 一、对面积的曲面积分的概念 二、对面积的曲面积分的性质 三、对面积的曲面积分的计算 四、对面积的曲面积分的应用
对面积的曲面积分 一、对面积的曲面积分的概念 二、对面积的曲面积分的性质 三、对面积的曲面积分的计算 四、对面积的曲面积分的应用

对面积的曲面积分 一、对面积的曲面积分的概念 二、对面积的曲面积分的性质 三、对面积的曲面积分的计算 四、对面积的曲面积分的应用
对面积的曲面积分 一、对面积的曲面积分的概念 二、对面积的曲面积分的性质 三、对面积的曲面积分的计算 四、对面积的曲面积分的应用

对面积的曲面积分的概念 (一) 1例 (二)对面积的曲面积分的定义
一、 对面积的曲面积分的概念 (一)引例 (二)对面积的曲面积分的定义

一、对面积的曲面积分的概念 (一) 3引例 (二)对面积的曲面积分的定义
一、 对面积的曲面积分的概念 (一)引例 (二)对面积的曲面积分的定义
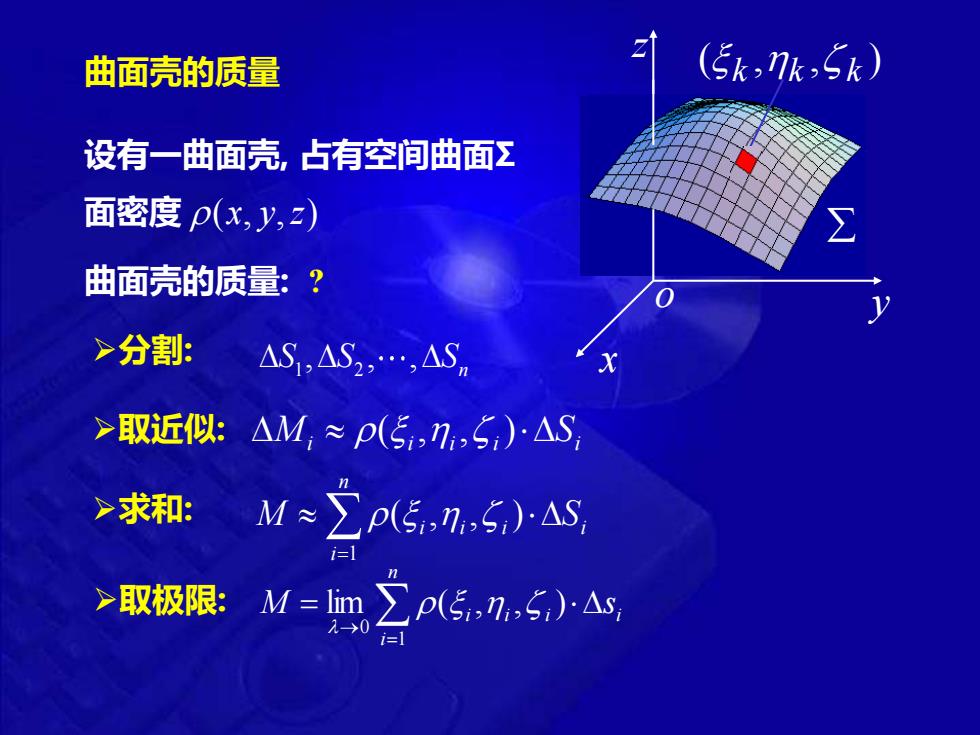
曲面壳的质量 (5k,7k,5k) 设有一曲面壳,占有空间曲面Σ 面密度p(x,y,) 曲面壳的质量:? >分割: △S,AS2,.ASn >取近似:△M,≈p(5,7,5)·△S >求和: M≈∑p5,n.5)AS ≥取极限:M=1m∑p5,7,5,)△s 2→0
曲面壳的质量 ➢分割: i i i i i M ( , , )S ➢求和: = n i i i i i M S 1 ( , , ) ➢取极限: = → = n i i i i i M s 1 0 lim ( , , ) ➢取近似: 面密度 (x, y,z) 设有一曲面壳, 占有空间曲面Σ 曲面壳的质量: ? 1 2 , , , n S S S o x y z ( , , ) k k k

一、对面积的曲面积分的概念 (一) 3引例 (二)对面积的曲面积分的定义
一、 对面积的曲面积分的概念 (一)引例 (二)对面积的曲面积分的定义

对面积的曲面积分的概念 (一) 3引例 (二)对面积的曲面积分的定义
一、 对面积的曲面积分的概念 (一)引例 (二)对面积的曲面积分的定义

>定义 设曲面是光滑的,函数fx,y,)在Σ上有界. 把Σ任意分成 小块△S(△S同时也代表第i小块的面积), 设(51,7,5) 是△S,上任意取定的一点,作乘积f(5,7,5)△S,(i=1,2,m 并作和之f(5,n,5,)△S,如果各小块曲面直径的最大值入助 这和的极限总存在,且与曲面的分法及点(5,的取法 无关,那么称此极限为函数孔xy)在曲面Σ上对面积的曲面 积分或第一类曲面积分,记作f(x,y,2)dS 即J∬fx,y,a)ds=lim∑f(5,n,5)△s, 230 其中飞,)叫做被积函数,Σ叫做积分曲面
➢定义 并作和 ( , , ) , 如果各小块曲面直径的最大值 时, 1 = n i i i i Si f 设曲面Σ是光滑的,函数f(x,y,z)在Σ上有界. 把Σ任意分成 n小块ΔSi (ΔSi同时也代表第i 小块的面积), 这和的极限总存在,且与曲面 的分法及点 的取法 f x y z S ( , , )d . 其中f(x,y,z)叫做被积函数,Σ叫做积分曲面. 是ΔSi上任意取定的一点, 设 ( , , ) i i i 作乘积 无关,那么称此极限为函数f(x,y, z)在曲面Σ上对面积的曲面 积分或第一类曲面积分,记作 即 0 1 ( , , )d ( , , ) . lim n i i i i i f x y z S f S → = = ( , , ) i i i

曲面壳的质量:M=川p(x,y,)ds ●注 (1)函数x,z)在闭曲面Σ上的曲面积分记为 月fk,3ds. (2)函数f孔x,z在光滑曲面Σ上连续时, fxyz)ds存在
曲面壳的质量: ( , , )d . M = x y z S ⚫注 (1) (2) 函数f(x,y,z)在光滑曲面Σ上连续时, f x y z S ( , , )d 存在. 函数f(x,y,z)在闭曲面Σ上的曲面积分记为 ( , , ) . f x y z dS