
第九讲 傅里计级数习题课
第九讲 傅里叶级数习题课

傅里叶级数习题课 一、内容小结 二、题型练习
傅里叶级数习题课 一、内容小结 二、题型练习

傅里叶级数习题课 一、内容小结 二、题型练习
傅里叶级数习题课 一、内容小结 二、题型练习
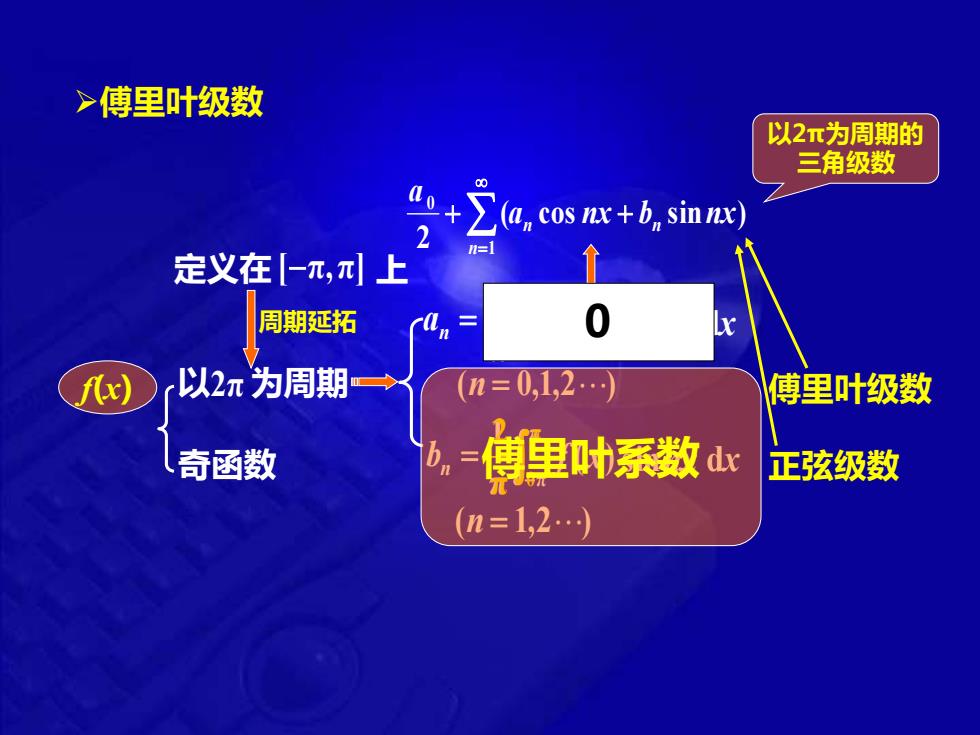
>傅里叶级数 以2π为周期的 三角级数 +∑(a,cos+b.si血) 2 定义在【-π,π上 周期延拓 0 fc) 以2元为周期→ (n=0,1,2 傅里叶级数 奇函数 傅里叶系数d山 正弦级数 (n=1,2
➢傅里叶级数 以 2π 为周期 ( cos sin ) 2 1 0 a nx b nx a n n n + + = 以2π为周期的 三角级数 f(x) (n = 0,1,2) an = − π π π 1 f (x) cosnx dx f (x)sinnx dx (n = 1,2) − π π π 1 bn = 傅里叶级数 定义在 [−π,π] 上 周期延拓 奇函数 0 π π 0 2 傅里叶系数 正弦级数

>傅里叶级数 以2π为周期的 三角级数 (a,cosnx+b,sinme) 定义在【-π,]上 周期延拓 an=兰lJc)cosd πAz fr) 以2π为周期→ (n=0,1,2.) 傅里叶级数 奇函数偶函数) 0 正弦级数 (n=1,2.) (余弦级数
➢傅里叶级数 以 2 为周期 ( cos sin ) 2 1 0 a nx b nx a n n n + + = 以2π为周期的 三角级数 f(x) (n = 0,1,2) an = − 1 f (x) cosnx dx f (x)sinnx dx (n = 1,2) − 1 bn = 傅里叶级数 定义在 [− , ] 上 周期延拓 奇函数(偶函数) 0 正弦级数 0 2 (余弦级数)
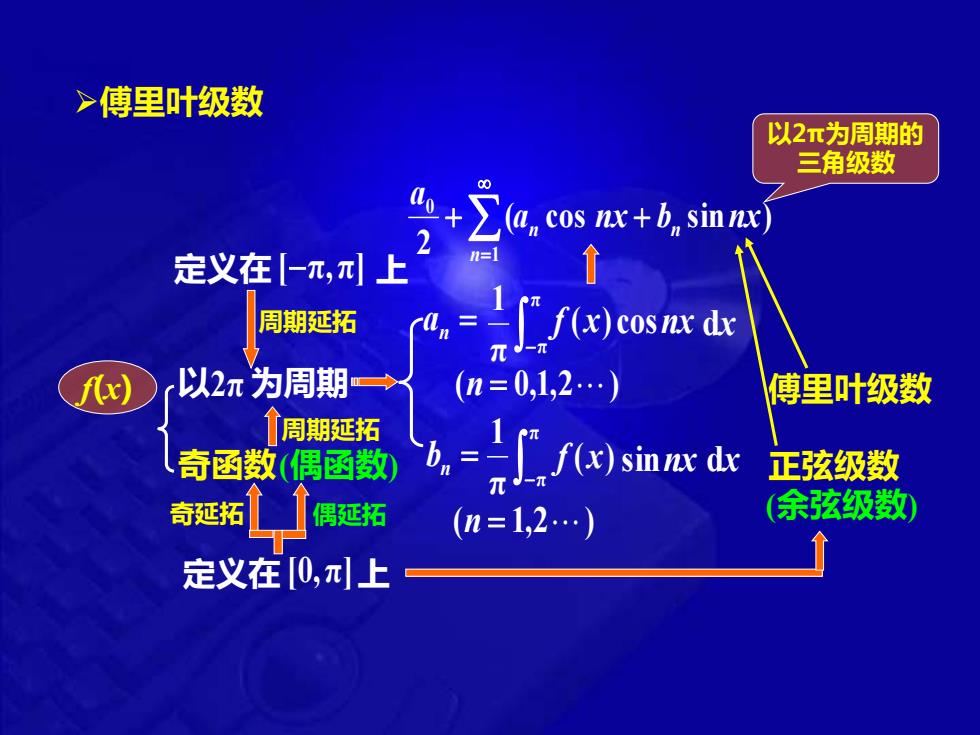
>傅里叶级数 以2π为周期的 三角级数 00 a,cosr+,sinj 定义在【-π,π上 周期延拓 ()cod 以2元为周期→ (n=0,1,2.) 傅里叶级数 周期延拓 奇函数密敲,b,=∫)sinn dx 正弦级数 奇延拓 偶延拓 (n=1,2.) (余弦级数 定义在[0,π上
➢傅里叶级数 以 2 π 为周期 ( cos sin ) 2 1 0 a nx b nx a n n n + + = 以2π为周期的 三角级数 f(x ) ( n = 0 , 1 , 2 ) a n = −π π π 1 f ( x ) cosnx dx f (x)sinnx dx (n = 1,2) −π π π 1 bn = 傅里叶级数 定义在 [ − π , π ] 上 周期延拓 奇函数 (偶函数 ) 正弦级数 (余弦级数 ) 定义在 [ 0 , π ] 上 奇延拓 偶延拓 周期延拓
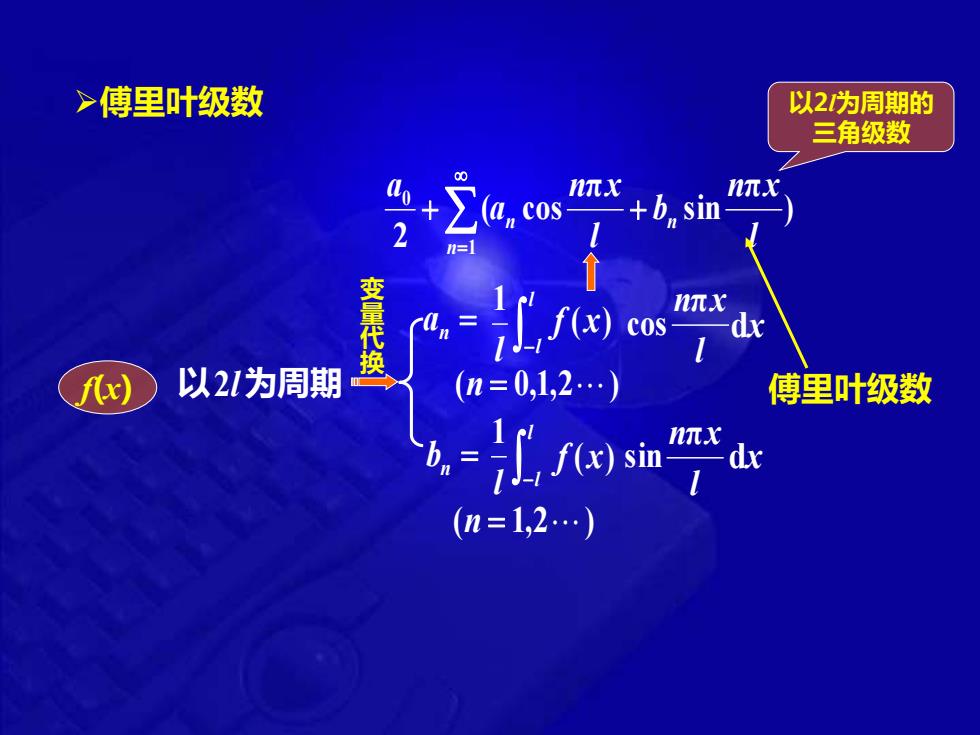
>傅里叶级数 以2为周期的 三角级数 +∑a,cs 元x tπx +b,sin 2 d 换 fx) 以21为周期 (n=0,1,2.) 傅里叶级数 (sin de (n=1,2.)
➢傅里叶级数 以 2 l 为周期 ) π sin π ( cos 2 1 0 l n x b l n x a a n n n + + = 以 2 l为周期的 三角级数 f(x ) ( n = 0 , 1 , 2 ) a n = −l l l1 l n π x f ( x ) cos dx f (x) dx l nπx sin (n = 1 , 2 ) −l l l1 b n = 傅里叶级数 变量代换

>傅里叶展开 收敛定理设f(x)是以21为周期的周期函数如果它满足: (1)在一个周期内连续或只有有限个第一类间断点, (2)在一个周期内至多只有有限个极值点, 则f(x)的傅里叶级数收敛,并且: 当x是fx)的连续点时,级数收敛于fx) 当x是孔x)的间断点时,级数收敛于 nel
➢傅里叶展开 收敛定理 设f (x)是以2l 为周期的周期函数,如果它满足: (1) 在一个周期内连续或只有有限个第一类间断点, (2) 在一个周期内至多只有有限个极值点, 则f (x) 的傅里叶级数收敛,并且: 当x是f(x)的连续点时,级数收敛于f(x); 当x是f(x)的间断点时,级数收敛于 ( ) ( ) 2 1 − + f x + f x

傅里叶级数习题课 一、内容小结 二、题型练习
傅里叶级数习题课 一、内容小结 二、题型练习

傅里叶级数习题课 一、内容小结 二、题型练三
傅里叶级数习题课 一、内容小结 二、题型练习