广东工业大学：《通信电路与系统》课程教学资源（课件讲义）第五章 正弦波振荡器 第三节 振荡器的频率稳定原理和高稳定度的LC振荡器

目录 5.1 概述与反馈型LC振荡原理 5.2 反馈型LC振荡电路 5.3 振荡器的频率稳定原理和高稳定度的LC振荡器 5.4 晶体振荡电路

目录 5.1 概述与反馈型LC振荡原理 5.2 反馈型LC振荡电路 5.3 振荡器的频率稳定原理和高稳定度的LC振荡器 5.4 晶体振荡电路

◇5.3振荡器的频率稳定原理 一、频率稳定度的定义 频率稳定度在数量上通常用频率偏差来表示。 频率偏差是指振荡器的实际工作频率和标称频率之间的偏差。它可 分为绝对偏差和相对偏差。 设f为实际振荡频率，f。为指定标称频率，则 1、绝对频率偏差：△f=f-f 绝对频率准确度 2、相对频率偏差：Y-/-1」 f。 f 相对频率准确度 3、频率稳定度的定义： 在一定时间间隔内，振荡器相对频率偏差的最大值，用3 表示。该数值越小越好，稳定性越高。 4、三种常用的频率稳定度 长期频率稳定度：一般指一天以上甚至数月的时间间隔内的相对频率变化的 最大值。这种变化通常是由振荡器中元器件老化而引起的。 短期频率稳定度：一般指一天以内，以小时、分或秒计算的时间间隔的频率 相对变化。产生这种频率不稳的因素有温度、电源电压等。 瞬时频率稳定度：一般指秒或毫秒时间间隔内的频率相对变化。引起这类频 率不稳定的主要因素是振荡器内部噪声

一、频率稳定度的定义 5.3 振荡器的频率稳定原理 频率稳定度在数量上通常用频率偏差来表示。 频率偏差是指振荡器的实际工作频率和标称频率之间的偏差。它可 分为绝对偏差和相对偏差。 设 f 为实际振荡频率，fc 为指定标称频率，则 1、绝对频率偏差： 2、相对频率偏差： c f  f  f c c c f f f f f |  |   3、频率稳定度的定义: 在一定时间间隔内，振荡器相对频率偏差的最大值，用 表示。该数值越小越好，稳定性越高。 max c f f  时间间隔 绝对频率准确度 相对频率准确度 4、三种常用的频率稳定度 长期频率稳定度：一般指一天以上甚至数月的时间间隔内的相对频率变化的 最大值。这种变化通常是由振荡器中元器件老化而引起的。 短期频率稳定度：一般指一天以内，以小时、分或秒计算的时间间隔的频率 相对变化。产生这种频率不稳的因素有温度、电源电压等。 瞬时频率稳定度：一般指秒或毫秒时间间隔内的频率相对变化。引起这类频 率不稳定的主要因素是振荡器内部噪声

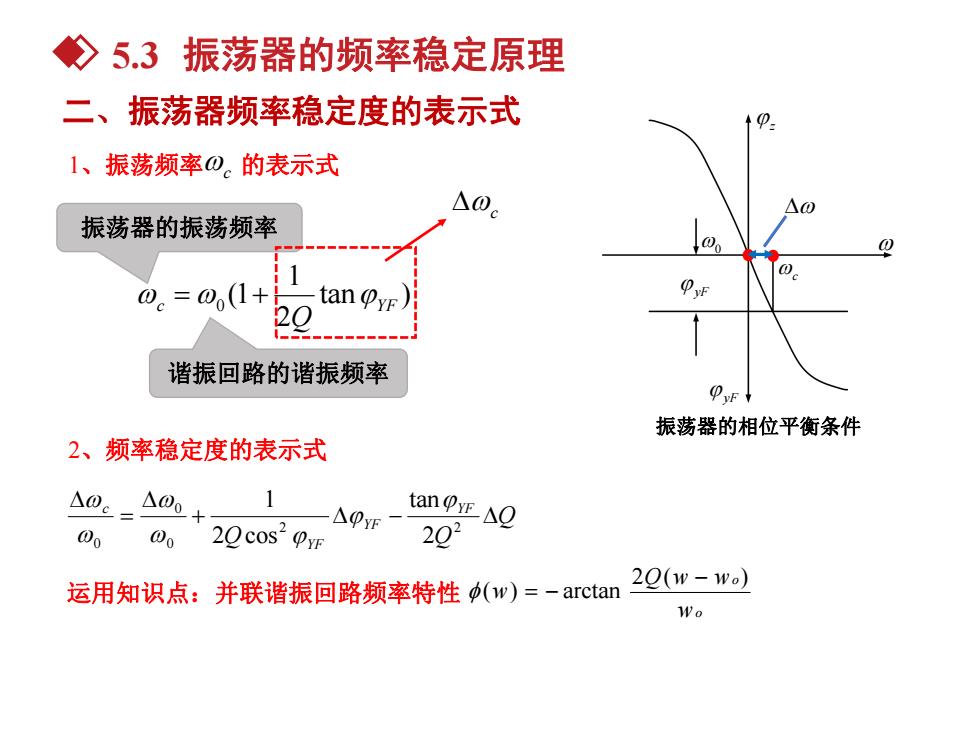
◇5.3振荡器的频率稳定原理 二、振荡器频率稳定度的表示式 1、振荡频率0。的表示式 △0 振荡器的振荡频率 0 0。=0(1+ tan PyF) 谐振回路的谐振频率 振荡器的相位平衡条件 2、频率稳定度的表示式 △0e_△0+ 1 一△pyF tan pyE△Q 00 @o 20cos2 Oyn 202 运用知识点：并联谐振回路频率特性(w)=-arctan 20(w-Wo) Wo

振荡器的相位平衡条件 z 0   yF  yF c 二、振荡器频率稳定度的表示式 振荡器的振荡频率 谐振回路的谐振频率 2、频率稳定度的表示式 tan ) 2 1 (1 c 0 YF Q      Q Q Q YF YF YF c        2 2 0 0 0 2 tan 2 cos 1        运用知识点：并联谐振回路频率特性 o o w Q w w w 2 ( ) ( ) arctan     1、振荡频率 c 的表示式 c  5.3 振荡器的频率稳定原理

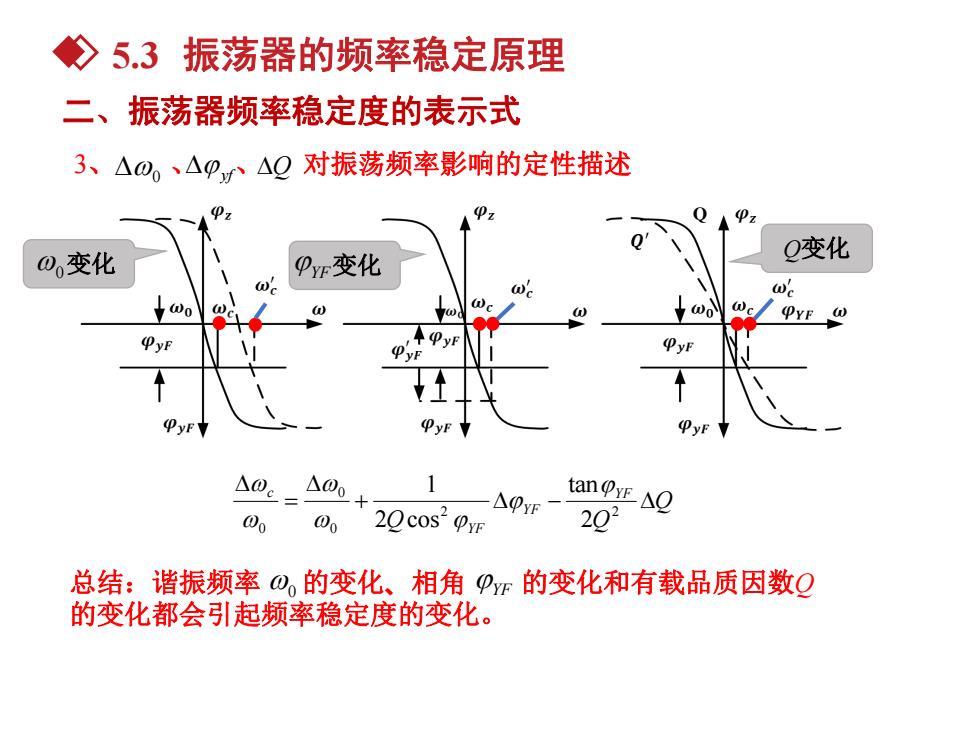
◇5.3振荡器的频率稳定原理 二、振荡器频率稳定度的表示式 3、△0，、△p,r、△Q对振荡频率影响的定性描述 0 (z 0,变化 Q变化 PF变化 @o ωo △0。_A00 一△F一 anyE△g 00 20cos yE 202 总结：谐振频率⊙，的变化、相角pF的变化和有载品质因数Q 的变化都会引起频率稳定度的变化

Q Q变化 Q Q Q YF YF YF c        2 2 0 0 0 2 tan 2 cos 1         0变化  YF 变化 总结：谐振频率 的变化、相角 的变化和有载品质因数Q 的变化都会引起频率稳定度的变化。 0 YF 3、  0 、 yf、 Q 对振荡频率影响的定性描述 5.3 振荡器的频率稳定原理 二、振荡器频率稳定度的表示式

◇5.3振荡器的频率稳定原理 三、引起频率不稳的原因 1、温度变化会引起L、C和晶体管参数变化。 2、湿度变化会引起L、Q变化。 3、电源电压变化会引起晶体管参数变化。 4、机械振动会引起L的变化。 结论：引起振荡器频率不稳定的外部因素是温度、湿度、电源电 压波动和机械振动。这些外因变化会引起△0。△p、△Q的变 化。因此产生频率不稳定

三、引起频率不稳的原因 1、温度变化会引起L、C和晶体管y参数变化。 2、湿度变化会引起L、Q变化。 3、电源电压变化会引起晶体管参数变化。 4、机械振动会引起L的变化。 结论：引起振荡器频率不稳定的外部因素是温度、湿度、电源电 压波动和机械振动。这些外因变化会引起 的变 化。因此产生频率不稳定。 0、YF、Q 5.3 振荡器的频率稳定原理

◇5.3振荡器的频率稳定原理 四、提高频率稳定度的措施 1.提高振荡回路的标准性：选择稳定度高的元件。 2.减少晶体管的影响：选择f较高的晶体管。 3.提高回路的品质因数：据LC回路的特性，Q值越大，相频特性斜 率就越大，相位越稳定。 4.减少电源、负载等的影响：电源电压的波动，会使晶体管的工作 点等变化，负载电阻会降低回路的品质因数。 5.选用高稳定度的振荡电路：如克拉波振荡电路、西勒振荡电路、 石英晶体振荡电路。 6.远离热源，屏蔽干扰源

四、提高频率稳定度的措施 1. 提高振荡回路的标准性：选择稳定度高的元件。 2. 减少晶体管的影响：选择fT较高的晶体管。 3. 提高回路的品质因数：据LC回路的特性，Q值越大，相频特性斜 率就越大，相位越稳定。 4. 减少电源、负载等的影响：电源电压的波动,会使晶体管的工作 点等变化，负载电阻会降低回路的品质因数。 5. 选用高稳定度的振荡电路：如克拉波振荡电路、西勒振荡电路、 石英晶体振荡电路。 6. 远离热源，屏蔽干扰源。 5.3 振荡器的频率稳定原理

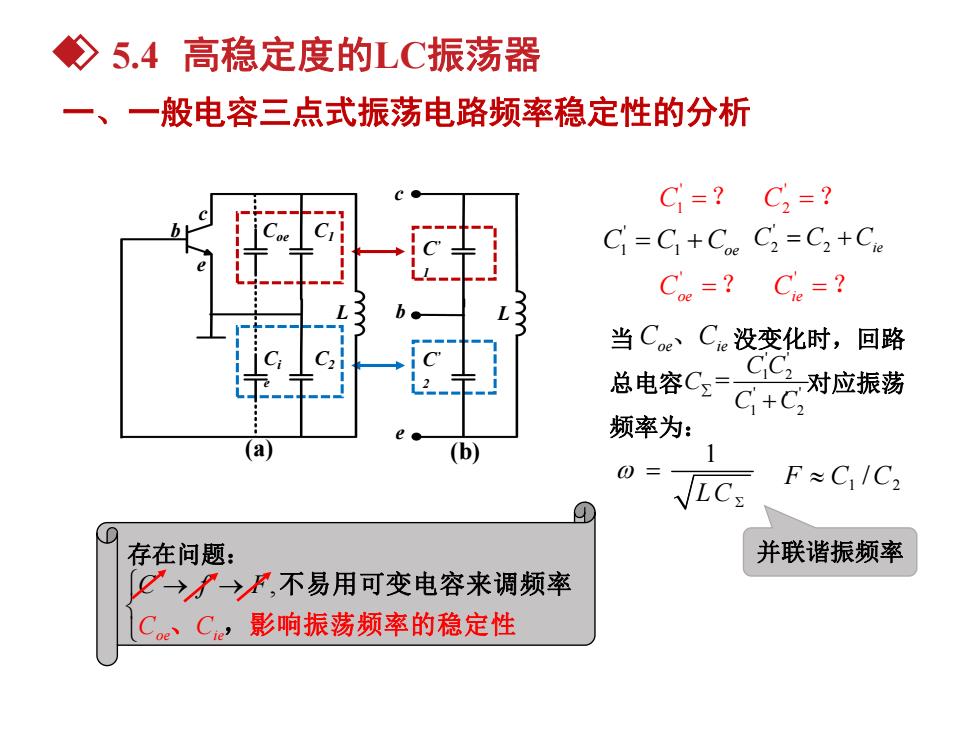
◇5.4高稳定度的LC振荡器 一、一般电容三点式振荡电路频率稳定性的分析 C=？C=? CI=C]+Coe C2=C2+Cie Ce=？ C=? 当CeCe没变化时，回路 总电容C CC2对应振荡 C+C 频率为： a LC F≈C1/C2 存在问题： 并联谐振频率 →/→，不易用可变电容来调频率 Ce、C。,影响振荡频率的稳定性

一、一般电容三点式振荡电路频率稳定性的分析 5.4 高稳定度的LC振荡器 并联谐振频率 1 LC    1 2 F  C /C ' C1  C1 Coe ' C2  C2 Cie ' ' C1 ？ C2 ？ ' ' Coe ？ Cie ？ 当 没变化时，回路 总电容 ，对应振荡 频率为： Coe、Cie ' ' 1 2 ' ' 1 2 = C C C C C   C’ 1 C’ 2 (a) (b) Coe C1 Ci C2 e b c e c b e L L 存在问题： , oe ie C f F C C      、 影响振荡频 不易用可变电容 率的稳定 来 率 性 调频

◇5.3高稳定度的LC振荡器 C、C影响振荡频率的稳定性分析 因Ce、C与晶体管工作状态和 外界条件有关。 当C变化AC。Ce变化△C △C。 时，总电容的增量： △Cy AC:P 'ACo+p2'AC P=？P2=? AC CC2 P1= p和p能否 C1+C2 同时变小？ (c) P2= C C ，C1+C2 结论：一般电容三点式振荡电路p、P2不可能同时减小，故受外界 影响后，振荡频率会发生变化，即-频率稳定度不可能做得较高

结论：一般电容三点式振荡电路p1、p2不可能同时减小，故受外界 影响后，振荡频率会发生变化，即-频率稳定度不可能做得较高。 因 与晶体管工作状态和 外界条件有关。 Coe、Cie 当 变化 变化 时，总电容的增量： Coe Co，Cie Ci O Ci C  p C  p  2 2 2 1 1 2 p ？ p ？ 1 2 2 1 1 C C C C C p         1 2 1 2 2 C C C C C p         ∆Co ∆Ci C’ 1 C’ 2 ∆C∑ (c) b L c e Coe、Ci e 影响振荡频率的稳定性分析 p1和p2能否 同时变小？ 5.3 高稳定度的LC振荡器

◇5.3高稳定度的LC振荡器 二、克拉泼(Clapp)振荡电路 属于哪种组态？ 共基型电路 1、电路特点 ①在电感支路串接小电容C? R10 R C3一般可调 C ②满足C3<C,C3<C2 可使回路与晶体管的输入、输 出参数隔开来，也就是实现晶 R20 Re 串入C3 体管与回路之间的松耦合。 [管子的内部参数对回路的影响 非常小] (a) ③回路总电容为： 克拉泼振荡电路 CCC = 和一般电容式振荡器有何区别？ C.=cC:+CC,+C℃ C≈C3

克拉泼振荡电路 1、电路特点 ①在电感支路串接小电容C3 C3一般可调 和一般电容式振荡器有何区别？ 串入C3 属于哪种组态？ 共基型电路 ③回路总电容为： 1 2 3 1 2 2 3 1 3 =? C C C C C C C C C C           C  C3 ②满足 可使回路与晶体管的输入、输 出参数隔开来，也就是实现晶 体管与回路之间的松耦合。 [管子的内部参数对回路的影响 非常小] 3 1 3 2 C  C ,C  C 二、克拉泼（Clapp）振荡电路 5.3 高稳定度的LC振荡器

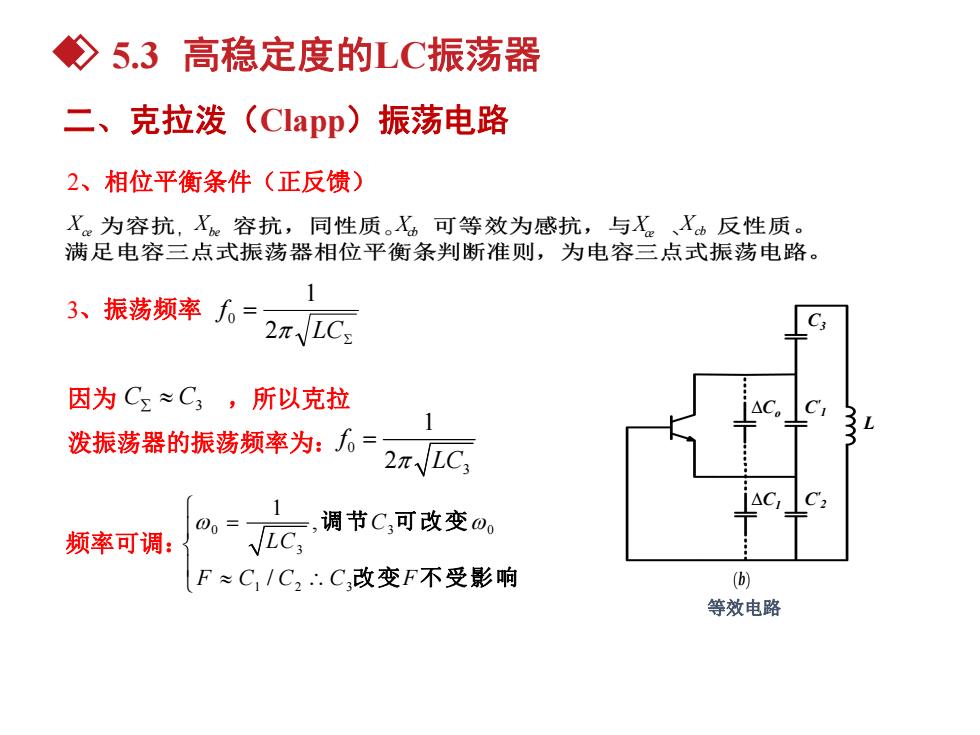
◇5.3高稳定度的LC振荡器 二、克拉泼(Clapp)振荡电路 2、相位平衡条件（正反馈） X。为容抗，X容抗，同性质。X可等效为感抗，与X、X反性质。 满足电容三点式振荡器相位平衡条判断准则，为电容三点式振荡电路。 3、振荡频率= 1 2LCs 因为CΣ≈C3,所以克拉 i△C。 C 泼振荡器的振荡频率为：%= 2πVLC △C,C2 00= ,调节C,可改变0， 频率可调： LC; F≈C,/C,∴.C,改变F不受影响 (b) 等效电路

2、相位平衡条件（正反馈） 频率可调： 等效电路 C′2 C′ ∆Co 1 ∆C1 C3 L Xce Xbe Xcb Xce Xcb 0 3 0 3 1 2 3 1 , / C LC F C C C F           调节 可改变 改变 不受影响 3、振荡频率 因为 ，所以克拉 泼振荡器的振荡频率为：   LC f 2 1 0 0 3 1 2 f  LC  C  C3 二、克拉泼（Clapp）振荡电路 5.3 高稳定度的LC振荡器