
目录 6.1 概论 6.4 单边带信号的产生 6.2 低电平调幅电路 6.5 包络检波器 6.3 高电平调幅电路
目录 6.1 概论 6.2 低电平调幅电路 6.3 高电平调幅电路 6.4 单边带信号的产生 6.5 包络检波器
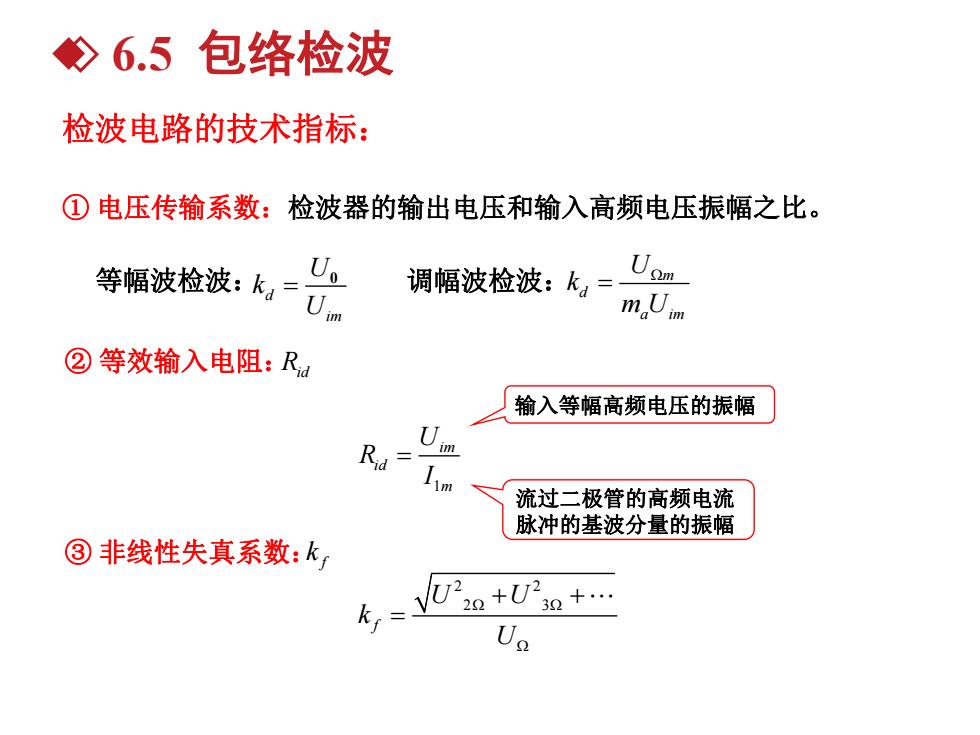
◇6.5包络检波 检波电路的技术指标: ①电压传输系数:检波器的输出电压和输入高频电压振幅之比。 等幅波检波:k,= Uo 调幅波检波:k= maUim ②等效输入电阻:Ra 输入等幅高频电压的振幅 Rid= 流过二极管的高频电流 脉冲的基波分量的振幅 ③非线性失真系数:k k=- +U2a+
6.5 包络检波 检波电路的技术指标: ① 电压传输系数:检波器的输出电压和输入高频电压振幅之比。 1 im id m U R I ② 等效输入电阻:Rid ③ 非线性失真系数: 2 2 2 3 f U U k U 输入等幅高频电压的振幅 流过二极管的高频电流 脉冲的基波分量的振幅 等幅波检波: d im U k U 0 调幅波检波: m d a im U k m U f k

◇6.5.1二极管大信号包络检波器 一、大信号包络检波 输入信号振幅大于0.5V,利用二极管两端加正向电压时导通,输入 信号电压通过二极管对低通滤波器的电容C充电。二极管两端加反向电 压时截止,电容C通过R放电这一特性实现的检波,其输出电压反映输 入信号振幅变化的规律。 二、大信号检波的工作原理 1.原理电路 下图是二极管大信号检波的原理电路,是输入回路、非线性器件和低通 滤波器组成 输入回路:相当于末级中放的输出 回路,输入AM信号 二极管D:相当于一个非线性元件 u(t 输出回路:低通RC滤波网络
6.5.1 二极管大信号包络检波器 输入信号振幅大于0.5V,利用二极管两端加正向电压时导通,输入 信号电压通过二极管对低通滤波器的电容C充电。二极管两端加反向电 压时截止,电容C通过R放电这一特性实现的检波,其输出电压反映输 入信号振幅变化的规律。 二、大信号检波的工作原理 1. 原理电路 下图是二极管大信号检波的原理电路,是输入回路、非线性器件和低通 滤波器组成 一、大信号包络检波 输入回路:相当于末级中放的输出 回路,输入AM 信号 二极管D:相当于一个非线性元件 输出回路:低通RC滤波网络

6.5.1二极管大信号包络检波器 RC网络的基本功能: 容抗 对低频调制信号4。,相当于检波负载即 R 对高频载波信号短路,即滤除高频信号,即 <<R @C 在理想情况下,RC网络的阻抗为: 高频 Z(0)=0 ZRC(@)= Z(2)=R 低频 RC网络对流过二极管D中的电流i,的各频率分量来说, 高频短路,而直流和低频C开路,呈现的阻抗为R
RC网络的基本功能: 低频 高频 容抗 1 R C 对高频载波信号短路,即滤除高频信号,即 u 对低频调制信号 ,相当于检波负载即 0 1 R C 在理想情况下,RC网络的阻抗为: 0 ( ) 0 ( ) ( ) RC Z Z Z R RC网络对流过二极管D中的电流 的各频率分量来说, 高频短路,而直流和低频 C开路,呈现的阻抗为R。 D i 6.5.1 二极管大信号包络检波器

◇6.5.1二极管大信号包络检波器 2.检波过程 ①输入为等幅波,设4,(t)=Usinw,t R。() 4:() 4(t) 实际应用中,由于正向导通 时间很短,放电时间常数又 远大于高频电压周期, 输入为等幅波的检波过程 4,()的起伏很小。 由uo=4,-u。,o>0则D导通,C快速充电; 0~t,二极管导通,对C充电,充电时常数很小,充电快。4D<0则 D截止,C慢速放电。 4~2,二极管截止,C通过R放电,放电时常数很大,放电慢。 2~t,二极管导通,又对C充电。 t~t4,二极管截止,C上电压对R放电。 如此反复,直到在一周内电容充电电荷量与放电电荷量相等,充放电 达到动态平衡进入稳定工作状态
如此反复,直到在一周内电容充电电荷量与放电电荷量相等,充放电 达到动态平衡进入稳定工作状态。 2. 检波过程 uO ①输入为等幅波,设 ( ) i im i u t U sinwt t2 ~ t3 ,二极管导通,又对 C 充电。 t3 ~ t4 ,二极管截止,C 上电压对 R 放电。 t1 ~ t2 ,二极管截止,C 通过 R 放电,放电时常数很大,放电慢。 ,二极管导通,对 C 充电,充电时常数很小,充电快。uD <0 则 D 截止,C 慢速放电。 0 ~ t1 由uD ui – uo ,uD 0 则 D 导通, C 快速充电; 实际应用中,由于正向导通 时间很短,放电时间常数又 远大于高频电压周期, uo (t) 的起伏很小。 6.5.1 二极管大信号包络检波器
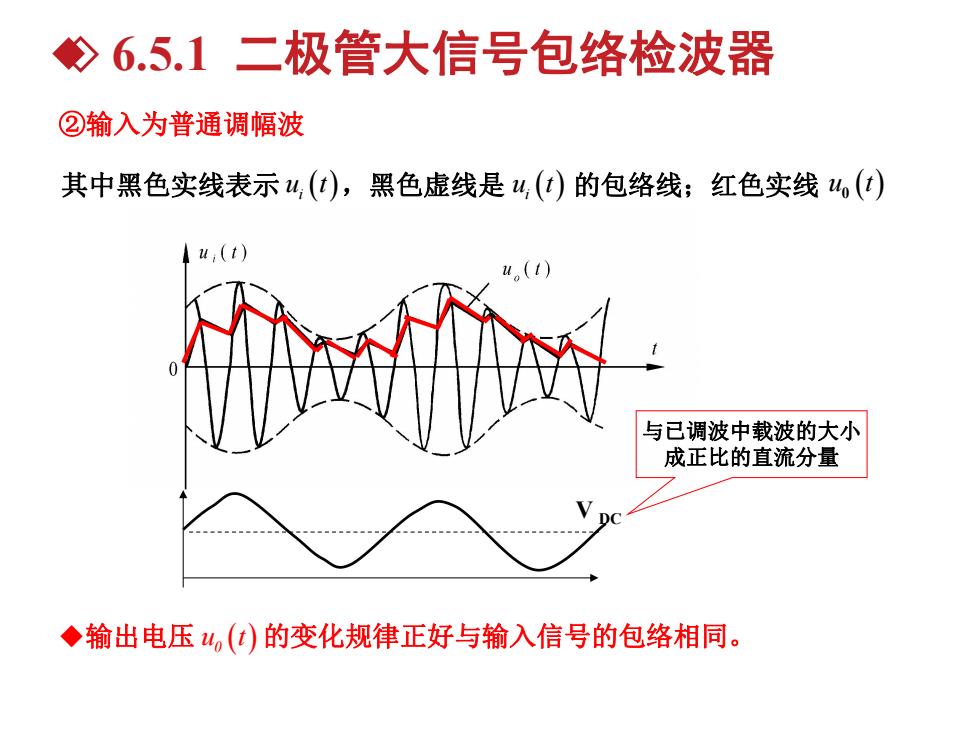
6.5.1二极管大信号包络检波器 ②输入为普通调幅波 其中黑色实线表示4,(t),黑色虚线是4,(t)的包络线;红色实线4(t) ,(t) u。(1) 与已调波中载波的大小 成正比的直流分量 ◆输出电压4(t)的变化规律正好与输入信号的包络相同
u输出电压 u0 t 的变化规律正好与输入信号的包络相同。 ②输入为普通调幅波 V DC 与已调波中载波的大小 成正比的直流分量 其中黑色实线表示 ,黑色虚线是 ui t 的包络线;红色实线 u t ui 0 t 6.5.1 二极管大信号包络检波器
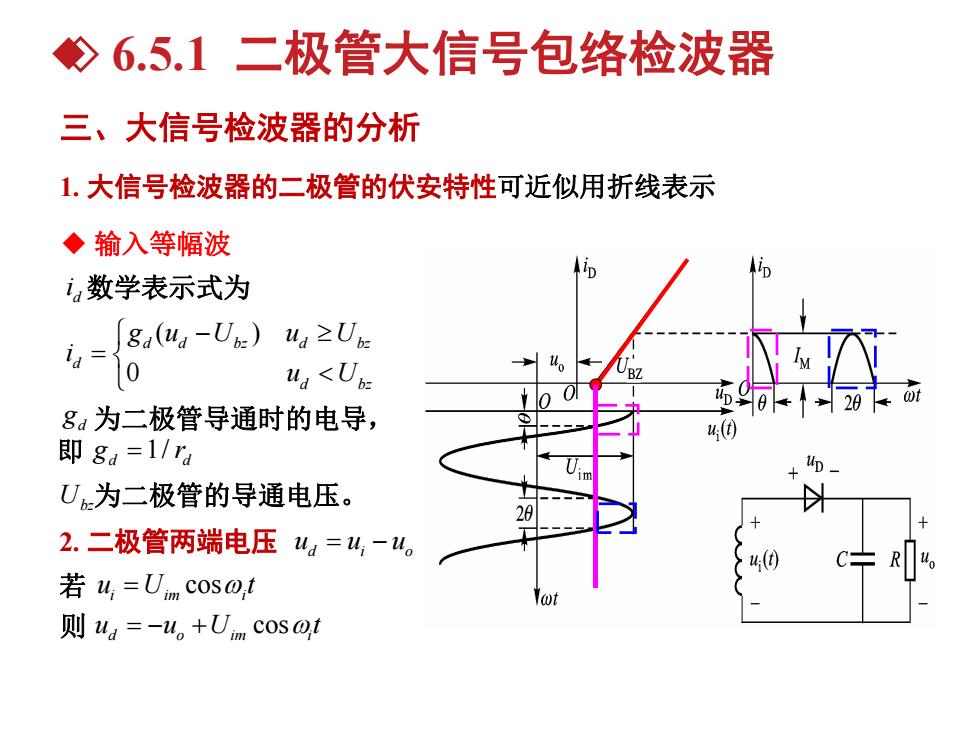
◇6.5.1二极管大信号包络检波器 三、大信号检波器的分析 1.大信号检波器的二极管的伏安特性可近似用折线表示 ◆输入等幅波 i数学表示式为 o 8a(ud-Um) ua≥U6e 10 ua <Uh 8为二极管导通时的电导, ( 即ga=1/ra m U为二极管的导通电压。 2.二极管两端电压u4=4,-u。 4( CR 若4,=Uim cos,t 则ua=-u。+Umc0so,t
d i o 2. 二极管两端电压 u u u cos i im i 若 u U t cos d o im i 则 u u U t 三、大信号检波器的分析 1. 大信号检波器的二极管的伏安特性可近似用折线表示 u 输入等幅波 id 数学表示式为 ( ) 0 d d bz d bz d d bz g u U u U i u U 为二极管导通时的电导, 即 d g 1/ d d g r Ubz为二极管的导通电压。 6.5.1 二极管大信号包络检波器
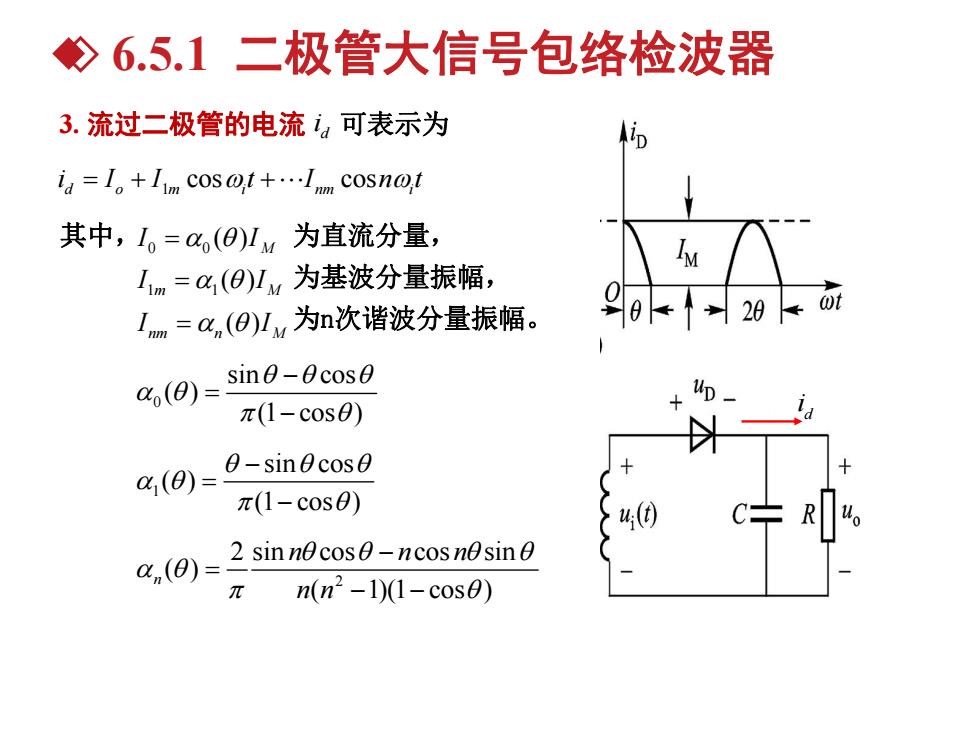
父 6.5.1二极管大信号包络检波器 3.流过二极管的电流可表示为 ia=I。+Iim cos0,t+…Im cosn0,t 其中,1。=(0)1M为直流分量, M Im=a(O)IM为基波分量振幅, Inm=a,(O)lw为n次谐波分量振幅。 200 (0)=sing-0cos0 π(1-cos0) a(0)-0-sinOcose π(1-cos0) t. R a,(0=2 sinnecos-ncosnsin π n(n2-1)1-cos0)
1 cos cos d o m i nm i i I I t I nt 3. 流过二极管的电流 id 可表示为 0 sin cos ( ) (1 cos ) 1 sin cos ( ) (1 cos ) 2 2 sin cos cos sin ( ) ( 1)(1 cos ) n n n n n n d i 其中,I 0 0 ( )I M 为直流分量, 1 1 ( ) m M I I 为基波分量振幅, ( ) nm n M I I 为n次谐波分量振幅。 6.5.1 二极管大信号包络检波器

◇6.5.1二极管大信号包络检波器 4.0与电路参数的关系 当ua>4e时,二极管导通,将ua=(-+COS@,t)代入二极管导通时 的方程 id =gd(ud-up)=gd (-uo+uim cosot-up) 当o,t=0时,i4=0,可得8a(-4+mc0s0,t-ue)=0 cos0=%。+U Uim 当0,t=0时,ia=IM,可得 gU(1-cos 由于1。=1wa(0),则 1,-g,4.(1-cos8)-1stn9-cos6--1Un(6n0-9cos9) π1-cos0 πra
cos o bz im u U U id gd ud ubz gd u0 uim cosit ubz 4. θ与电路参数的关系 1 sin cos 1 1 cos (sin cos ) 1 cos o d im im d I g u U r 由于 I o IM 0 ,则 当 时,二极管导通,将 代入二极管导通时 的方程 ud ubz ud u0 uim cosit 0 ( ) 1 (1 cos ) bz o M d im bz d im d im im U u I g u U U g U g U U 当 时,id 0 ,可得 0 cos 0 d im i bz g u u t u i t 当it 0 时,id IM ,可得 6.5.1 二极管大信号包络检波器

6.5.1二极管大信号包络检波器 经低通滤波器的输出电压L,=1,R=RU,sin0-0cos) πrA 因为0为未知数,不可能直接求解,还需变换,上式两边同时除cos0, 则 4-RU.an0-0=,4-R(tan0-9 ho+Ubzπra uo+Ub2πa Uim 当U2=0,或者4,>Uz的条件下,可得anB-日=a 当0<2rad时,tam可展开为tam0=0+g 6 15 可忽略 可得:0≈ R 结论:①在Ue=0,0<严ad 的条件下,其通角0只与电路参数a和R 6 有关,而与输入信号的振幅Um无关, ②输入等幅波时,输出直流电压:U。=Ucos0
经低通滤波器的输出电压 0 0 (sin cos ) im d R u I R U r 因为 为未知数,不可能直接求解,还需变换,上式两边同时除 , 则 cos 0 0 0 0 (tan ) (tan ) im bZ d bZ d im u R u R U u U r u U r U d bZ 0 bZ πr U = 0 u >>U tan θ - θ = R 当 ,或者 的条件下,可得 1 3 2 5 6 3 15 θ < rad tanθ tanθ = θ+ θ + θ +.... 当 时, 可展开为 3 3 dr R 可得: 结论:① 在 的条件下,其通角θ只与电路参数 和 有关,而与输入信号的振幅 无关. 0, 6 Ubz rad dr Uim R ② 输入等幅波时,输出直流电压: cos UO Uim 可忽略 6.5.1 二极管大信号包络检波器