
第五章消息认证算法 内容提要 95.1消息认证码 95.2杂凑函数 95.3MD5杂凑算法 95.4安全杂凑算法SHA 95.5SHA-3(Keccak算法)简介 5.6 HMAC 历粤花子代技大 21
内容提要 5.1 消息认证码 5.2 杂凑函数 5.3 MD5杂凑算法 5.4 安全杂凑算法SHA 5.5 SHA-3(Keccak算法)简介 5.6 HMAC 2/ 第五章 消息认证算法

第五章消息认证算法:5.1消息认证码 5.1消息认证码 消息认证的作用和含义: 消息认证用以验证接收消息的如下属性: 真实性(的确是由它所声称的实体发来的:消息源认证) 完整性(未被篡改、插入、删除) 消息的顺序性和时间性(未重排、重放、延迟) 。业务的不可否认性(即防止通信双方中的某一方对所传输消息 的否认) ·实现消息的不可否认性可通过数字签字,数字签字也是一种 认证技术,它也可用于抗击主动攻击 消息认证是抗主动攻击的关键技术 历粤毛子代枝大学 3/
5.1 消息认证码 消息认证的作用和含义: 消息认证用以验证接收消息的如下属性: ⚫ 真实性(的确是由它所声称的实体发来的:消息源认证) ⚫ 完整性(未被篡改、插入、删除) ⚫ 消息的顺序性和时间性(未重排、重放、延迟) ⚫ 业务的不可否认性(即防止通信双方中的某一方对所传输消息 的否认) ⚫ 实现消息的不可否认性可通过数字签字,数字签字也是一种 认证技术,它也可用于抗击主动攻击 消息认证是抗主动攻击的关键技术 3/ 第五章 消息认证算法:5.1 消息认证码

第五章消息认证算法:5.1消息认证码 5.1.1消息认证码的定义及使用方式 ·消息认证机制和数字签字机制需要有产生认证符的基本 功能 。这一基本功能又作为认证协议的一个组成部分 认证符是用于认证消息的数值,经过压缩函数计算而得 认证符的产生有两大类 ·消息认证码:MAC(Message Authentication Code) 。 杂凑函数(也称散列函数,hash function) 。消息认证码MAC指消息被一密钥控制的公开函数作用 后产生的、用作认证符的、固定长度的数值,也称为密 码校验和 ●此时需要通信双方A和B共享一密钥k 历些毛子代枚大学 4/
5.1.1 消息认证码的定义及使用方式 消息认证机制和数字签字机制需要有产生认证符的基本 功能 ⚫ 这一基本功能又作为认证协议的一个组成部分 ⚫ 认证符是用于认证消息的数值,经过压缩函数计算而得 ⚫ 认证符的产生有两大类 ⚫ 消息认证码:MAC(Message Authentication Code) ⚫ 杂凑函数(也称散列函数,hash function) 消息认证码MAC指消息被一密钥控制的公开函数作用 后产生的、用作认证符的、固定长度的数值,也称为密 码校验和 ⚫ 此时需要通信双方A和B共享一密钥k 4/ 第五章 消息认证算法:5.1 消息认证码
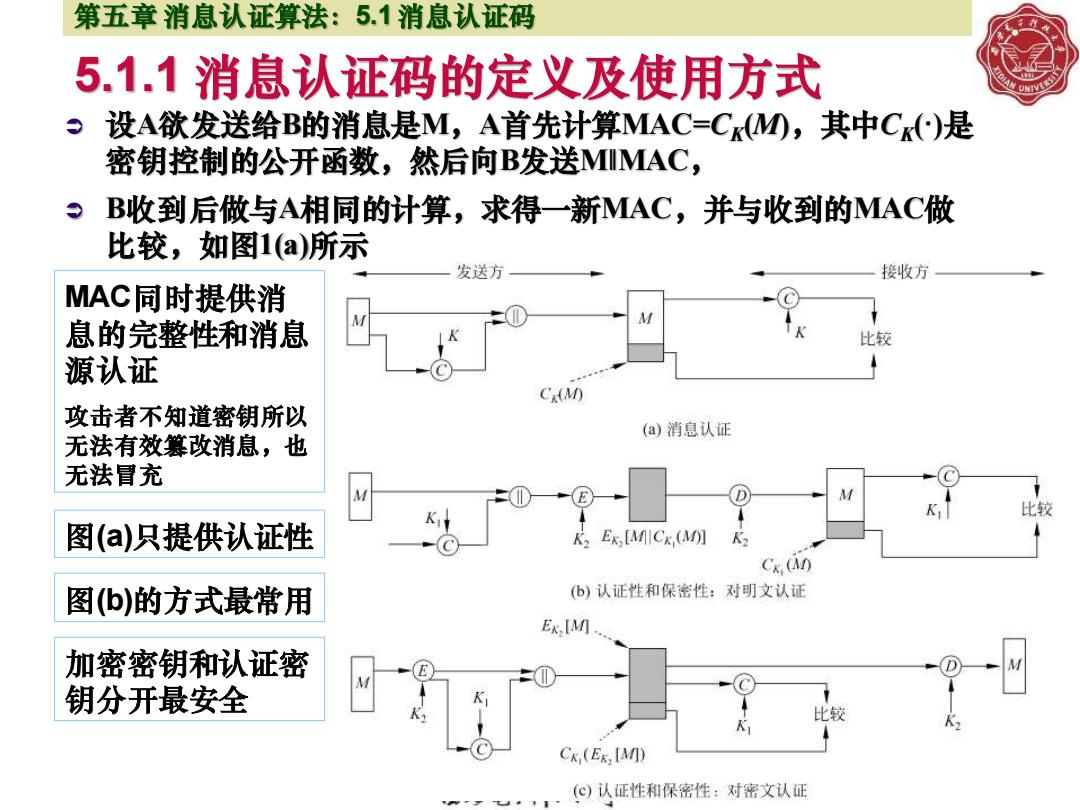
第五章消息认证算法:5.1消息认证码 5.1.1消息认证码的定义及使用方式 设A欲发送给B的消息是M,A首先计算MAC=C(M,其中C)是 密钥控制的公开函数,然后向B发送MMAC, 9 B收到后做与A相同的计算,求得一新MAC,并与收到的MAC做 比较,如图1(a)所示 发送方 接收方 MAC同时提供消 息的完整性和消息 比较 源认证 C(M) 攻击者不知道密钥所以 (a)消息认证 无法有效篡改消息,也 无法冒充 比较 图(a)只提供认证性 EK [MICK,(M)] K Ck (M) 图(b)的方式最常用 (b)认证性和保密性:对明文认证 Ex.[M] 加密密钥和认证密 钥分开最安全 比钗 CK (EK,[MD) (©)认证性和保密性:对密文认证
5.1.1 消息认证码的定义及使用方式 设A欲发送给B的消息是M,A首先计算MAC=CK(M),其中CK(·)是 密钥控制的公开函数,然后向B发送M‖MAC, B收到后做与A相同的计算,求得一新MAC,并与收到的MAC做 比较,如图1(a)所示 5/ 第五章 消息认证算法:5.1 消息认证码 MAC同时提供消 息的完整性和消息 源认证 攻击者不知道密钥所以 无法有效篡改消息,也 无法冒充 图(b)的方式最常用 图(a)只提供认证性 加密密钥和认证密 钥分开最安全

第五章消息认证算法:5.1消息认证码 5.1.1消息认证码的定义及使用方式 ·MAC算法与加密算法不同 MAC函数与加密算法的不同之处为MAC函数不必是可逆的,因 此与加密算法相比更不易被攻破 加密算法依赖于密钥长度,如果加密算法没有弱点,则敌手只 能使用穷搜索攻击,直到得到有意义的明文 加密密钥和认证密钥不同时安全性最高 如果二者相同,则对保密性的破译,同时也就是对认证性的破 译,这时有效密钥长度至多为一个密钥的长度。也可以把认证 和保密算法看成是单一密钥控制下的一个算法 因此加密密钥与认证密钥相同则实际上降低了总的安全性。 由MAC与加密算法的不同也可以看出,对加密密钥的破泽比对 消息认证码的破译要容易的多 历要荒子代枝七学 6/
5.1.1 消息认证码的定义及使用方式 MAC算法与加密算法不同 ⚫ MAC函数与加密算法的不同之处为MAC函数不必是可逆的,因 此与加密算法相比更不易被攻破 ⚫ 加密算法依赖于密钥长度,如果加密算法没有弱点,则敌手只 能使用穷搜索攻击,直到得到有意义的明文 加密密钥和认证密钥不同时安全性最高 ⚫ 如果二者相同,则对保密性的破译,同时也就是对认证性的破 译,这时有效密钥长度至多为一个密钥的长度。也可以把认证 和保密算法看成是单一密钥控制下的一个算法 ⚫ 因此加密密钥与认证密钥相同则实际上降低了总的安全性。 ⚫ 由MAC与加密算法的不同也可以看出,对加密密钥的破译比对 消息认证码的破译要容易的多 6/ 第五章 消息认证算法:5.1 消息认证码

第五章消息认证算法:5.1消息认证码 5.1.2产生MAC的函数应满足的要求 ·消息认证码的破译比加密算法的破译更难 9消息认证码MAC,其产生函数一般都为多到一映射 如果产生比特长的MAC,则函数的取值范围即为2"个可能的 MAC ● 函数输入可能的消息个数N>>2,而且如果函数所用的密钥为k 比特,则可能的密钥个数为2。 。如果系统不考虑保密性,即敌手能获取明文消息和相应的MAC 0 那么在这种情况下要考虑敌手使用穷搜索攻击来获取产生 MAC的函数所使用的密钥 。一种穷搜索攻击 假定k>n,且敌手已得到M和MAC1,其中MAC1=Ck(M1),敌 手对所有可能密钥值K求MAC=C(M),直到找到K使得 MAC=MACI 历些毛子代枚大学 71
5.1.2 产生MAC的函数应满足的要求 消息认证码的破译比加密算法的破译更难 消息认证码MAC,其产生函数一般都为多到一映射 ⚫ 如果产生n比特长的MAC,则函数的取值范围即为2 n个可能的 MAC ⚫ 函数输入可能的消息个数N>>2n,而且如果函数所用的密钥为k 比特,则可能的密钥个数为2 k 。 ⚫ 如果系统不考虑保密性,即敌手能获取明文消息和相应的MAC ,那么在这种情况下要考虑敌手使用穷搜索攻击来获取产生 MAC的函数所使用的密钥 一种穷搜索攻击 ⚫ 假定k>n,且敌手已得到M1和MAC1,其中MAC1=CK1(M1 ),敌 手对所有可能密钥值Ki求MACi=CKi(M1 ),直到找到Ki使得 MACi=MAC1 7/ 第五章 消息认证算法:5.1 消息认证码

第五章消息认证算法:5.1消息认证码 5.1.2产生MAC的函数应满足的要求 由于>n,2k个密钥仅能产生2"个不同的MAC,所以有很多密钥( 平均有22"=2-"个)都可产生出正确的MAC1,而敌手无法判断哪 个密钥正确,还必须按以下方式重复上述攻击: 第1轮已知M1、MAC1,其中MAC1=Cx(M1)。对所有2个可能 的密钥计算MAC=C(M),得2k-n个可能的密钥 第2轮已知M2MAC2,其中MAC2=CM2)。对上一轮得到的 2k个可能的密钥计算MAC=Ck(M2),得2k-2×n个可能的密钥 ·如此下去,如果仁,则上述攻击方式平均需要a轮。例如,密 钥长为80比特,MAC长为32比特,则第1轮将产生大约248个可 能密钥,第2轮将产生216个可能的密钥,第3轮即可找出正确的 密钥 ·如果密钥长度小于MAC的长度,k<,则第1轮就有可能找出正确 的密钥,也有可能找出多个可能的密钥,如果是后者,则仍需执 行第2轮搜索 历些毛子代枚大学 8/
5.1.2 产生MAC的函数应满足的要求 ⚫ 由于k>n,2 k个密钥仅能产生2 n个不同的MAC,所以有很多密钥( 平均有2 k /2n=2k-n个)都可产生出正确的MAC1,而敌手无法判断哪 个密钥正确,还必须按以下方式重复上述攻击: ⚫ 第1轮 已知M1、MAC1,其中MAC1=CK(M1 )。对所有2 k个可能 的密钥计算MACi=CKi(M1 ),得2 k-n个可能的密钥 ⚫ 第2轮 已知M2、MAC2,其中MAC2=CK(M2 )。对上一轮得到的 2 k-n个可能的密钥计算MACi=CKi(M2 ),得2 k-2×n个可能的密钥 ⚫ 如此下去,如果k=αn,则上述攻击方式平均需要α轮。例如,密 钥长为80比特,MAC长为32比特,则第1轮将产生大约2 48个可 能密钥,第2轮将产生2 16个可能的密钥,第3轮即可找出正确的 密钥 ⚫ 如果密钥长度小于MAC的长度,k<n,则第1轮就有可能找出正确 的密钥,也有可能找出多个可能的密钥,如果是后者,则仍需执 行第2轮搜索 8/ 第五章 消息认证算法:5.1 消息认证码

第五章消息认证算法:5.1消息认证码 5.1.2产生MAC的函数应满足的要求 ·所以对消息认证码的穷搜索攻击比对使用相同长度密钥的 加密算法的穷搜索攻击的代价还要大(所以加密和认证密 钥不能同) 然而有些攻击方法不需要寻找产生MAC的密钥 例如,设M=(XX,.X,m)是由64比特长的分组X=1,…,m)链接得 到的,其消息认证码由以下方式得到: 04(M0=X⊕X2⊕..⊕Xm CK(M)=EKIA(M)] ·其中⊕表示异或运算,加密算法是电码本模式的DES 。密钥长为56比特,MAC长为64比特 历粤毛子代牧大学 9/
5.1.2 产生MAC的函数应满足的要求 所以对消息认证码的穷搜索攻击比对使用相同长度密钥的 加密算法的穷搜索攻击的代价还要大(所以加密和认证密 钥不能同) 然而有些攻击方法不需要寻找产生MAC的密钥 ⚫ 例如,设M=(X1 ‖X2 ‖…‖Xm)是由64比特长的分组Xi (i=1,…,m)链接得 到的,其消息认证码由以下方式得到: ⚫ Δ(M)=X1X2…Xm ⚫ CK(M)=EK[Δ(M)] ⚫ 其中表示异或运算,加密算法是电码本模式的DES ⚫ 密钥长为56比特,MAC长为64比特 9/ 第五章 消息认证算法:5.1 消息认证码

第五章消息认证算法:5.1消息认证码 5.1.2产生MAC的函数应满足的要求 如果敌手得到MCx(M),那么敌手使用穷搜索攻击寻找 K将需做256次加密 然而敌手还可用以下方式攻击系统: 。将X到Xm1分别用自己选取的Y到Y,m1替换 ·求出Ym=Y田Y2⊕..⊕Ym-1⊕A(M,并用Ym替换Xm。 因此敌手可成功伪造一新消息M=Y⊕Y2⊕.⊕Ym,且M的 MAC与原消息M的MAC相同 历些鼋子代枝大学 10/
5.1.2 产生MAC的函数应满足的要求 ⚫ 如果敌手得到M‖CK(M),那么敌手使用穷搜索攻击寻找 K将需做2 56次加密 ⚫ 然而敌手还可用以下方式攻击系统: ⚫ 将X1到Xm-1分别用自己选取的Y1到Ym-1替换 ⚫ 求出Ym =Y1Y2 …Ym-1Δ(M),并用Ym替换Xm。 ⚫ 因此敌手可成功伪造一新消息M=Y1Y2 …Ym,且M的 MAC与原消息M的MAC相同 10/ 第五章 消息认证算法:5.1 消息认证码

第五章消息认证算法:5.1消息认证码 5.1.2产生MAC的函数应满足的要求 。 考虑到MAC所存在的以上攻击类型,可知它应满足以下要求,其中 假定敌手知道函数C,但不知道密钥K: ①如果敌手得到M和C(M),则构造一满足Ck(M')=CM)的新消息 M'在计算上是不可行的 敌手不需找出密钥K,而伪造一个与截获的MAC相匹配的新消息 在计算上是不可行的 ②Cx(M)在以下意义下是均匀分布的:随机选取两个消息M、M, Pr[Cx(M)=C(M)=2-",其中n为MAC的长 ·第2个要求是说敌手如果截获一个MAC,则伪造一个相匹配的 消息的概率为最小 ③若M是M的某个变换,即M=jM),例如为插入一个或多个比 特,那么PrCx(M)=CK(M')=2" 函数C不应在消息的某个部分或某些比特弱于其他部分或其他比 特,否则敌手获得M和MAC后就有可能修改M中弱的部分,从 而伪造出一个与原MAC相匹配的新消息 历毛子代枝大兽 11/
5.1.2 产生MAC的函数应满足的要求 考虑到MAC所存在的以上攻击类型,可知它应满足以下要求,其中 假定敌手知道函数C,但不知道密钥K: ⚫ ① 如果敌手得到M和CK(M),则构造一满足CK(M)=CK(M)的新消息 M 在计算上是不可行的 ⚫ 敌手不需找出密钥K, 而伪造一个与截获的MAC相匹配的新消息 在计算上是不可行的 ⚫ ② CK (M)在以下意义下是均匀分布的:随机选取两个消息M、M , Pr[CK(M)=CK(M)]=2-n,其中n为MAC的长 ⚫ 第2个要求是说敌手如果截获一个MAC,则伪造一个相匹配的 消息的概率为最小 ⚫ ③ 若M是M的某个变换,即M=f(M),例如f为插入一个或多个比 特,那么Pr[CK (M)=CK (M)]=2-n ⚫ 函数C不应在消息的某个部分或某些比特弱于其他部分或其他比 特,否则敌手获得M和MAC后就有可能修改M中弱的部分,从 而伪造出一个与原MAC相匹配的新消息 11/ 第五章 消息认证算法:5.1 消息认证码