
第三讲无线信源与信道 编码
第三讲 无线信源与信道 编码

三种编码技术 信源编码: 以提高通信有效性为目的的编码。 ■通常通过压缩信源的冗余度来实现。采用的一般方法是压缩每个 信源符号的平均比特数或信源的码率。即同样多的信息用较少的 码率传送,使单位时间内传送的平均信息量增加,从而提高通信 的有效性。 信道编码: ■是以提高信息传输的可靠性为目的的编码。 。通常通过增加信源的冗余度来实现。采用的一般方法是增大码率/ 带宽。与信源编码正好相反。 冬密码: ■是以提高通信系统的安全性为目的的编码。 通常通过加密和解密来实现。从信息论的观点出发“加密”可视 为增熵的过程.“解密”可视为减熵的过程。 Mobile Communication Theory
2 三种编码技术 v 信源编码: § 以提高通信有效性为目的的编码。 § 通常通过压缩信源的冗余度来实现。采用的一般方法是压缩每个 信源符号的平均比特数或信源的码率。即同样多的信息用较少的 码率传送,使单位时间内传送的平均信息量增加,从而提高通信 的有效性。 v 信道编码: § 是以提高信息传输的可靠性为目的的编码。 § 通常通过增加信源的冗余度来实现。采用的一般方法是增大码率/ 带宽。与信源编码正好相反。 v 密码: § 是以提高通信系统的安全性为目的的编码。 § 通常通过加密和解密来实现。从信息论的观点出发“加密”可视 为增熵的过程,“解密”可视为减熵的过程。 Mobile Communication Theory

内容 信源编码 冬分组码 冬卷积码 Turbo编码 Mobile Communication Theory
3 内容 v信源编码 v分组码 v卷积码 vTurbo编码 Mobile Communication Theory

基本概念 ”自信息量 对离散信源而言,信源x=[x,x,,x]的概率分布为P(x),P(x),…,P(x) ,则称 I(P(x,))=logz (1/P(x))=-logz(P(x,)) 为消息x,的自信息量,它具有随机变量的性质,但自信息量不能表示 信源总体的不定度。 信息熵 信息熵表示信源总体的不定度。它定义为信源信息的平均自信息量, 即 H()=E[I(P()] =-2P)e:Ps》 熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。 Mobile Communication Theory
4 基本概念 v 自信息量 对离散信源而言,信源 的概率分布为 ,则称 为消息 的自信息量,它具有随机变量的性质,但自信息量不能表示 信源总体的不定度。 v 信息熵 信息熵表示信源总体的不定度。它定义为信源信息的平均自信息量, 即 熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。 Mobile Communication Theory P x P x P x 1 2 , , , n I P x P x P x i i i log 1/ log 2 2 i x 2 1 log i n i i i H E I P x P x P x x x x x x 1 2 , , , n
无失真信源编码 信源符号 信源符号 等长偏码 变长编码 出现概率 CI C2 A 0.6 00 0 变长编码的思路: B 0.25 01 10 概率大用短码, 概率小用长码 0.1 10 110 D 0.05 11 1110 。 码字平均长度:R-之p(a,)K, 编码效率: n=- (X) R 信源 信源 信道 (A,B,C,D) 解码 信宿 编码器 Error:10-4
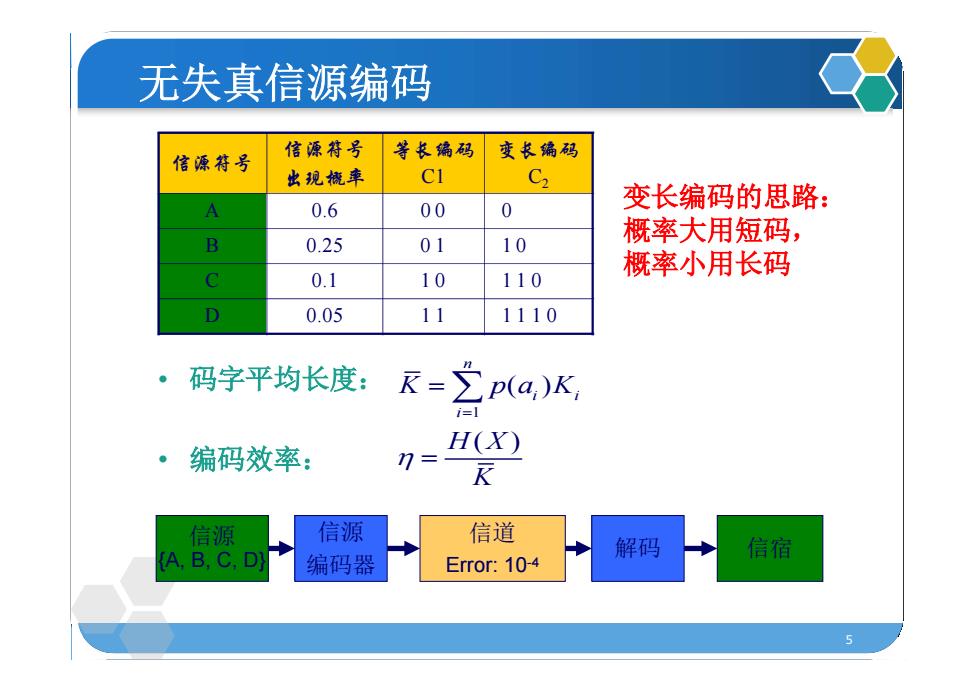
5 信源 {A, B, C, D} 信源 编码器 信道 Error: 10-4 解码 信宿 无失真信源编码 信源符号 信源符号 出现概率 等长编码 C1 变长编码 C2 A 0.6 0 0 0 B 0.25 0 1 1 0 C 0.1 1 0 1 1 0 D 0.05 1 1 1 1 1 0 • 码字平均长度: • 编码效率: 1 ( ) ( ) n i i i K p a K H X K 变长编码的思路: 概率大用短码, 概率小用长码
码字比较 倍源符号 信源符号 等长偏码 变长编码 信息熵 出现概率 CI C2 A 0.6 00 0 H(X)=-∑P(s)Iog,(P()月 2 0.25 01 10 0.1 10 110 =1.4905bit/符号 D 0.05 11 1110 平均码字长度 E1=2×0.6+2×0.25+2×0.1+2×0.05=2 2=1×0.6+2×0.25+3×0.1+4×0.05=1.6 ·编码效率, =H0=74.52% %=I0=93.16% K 6
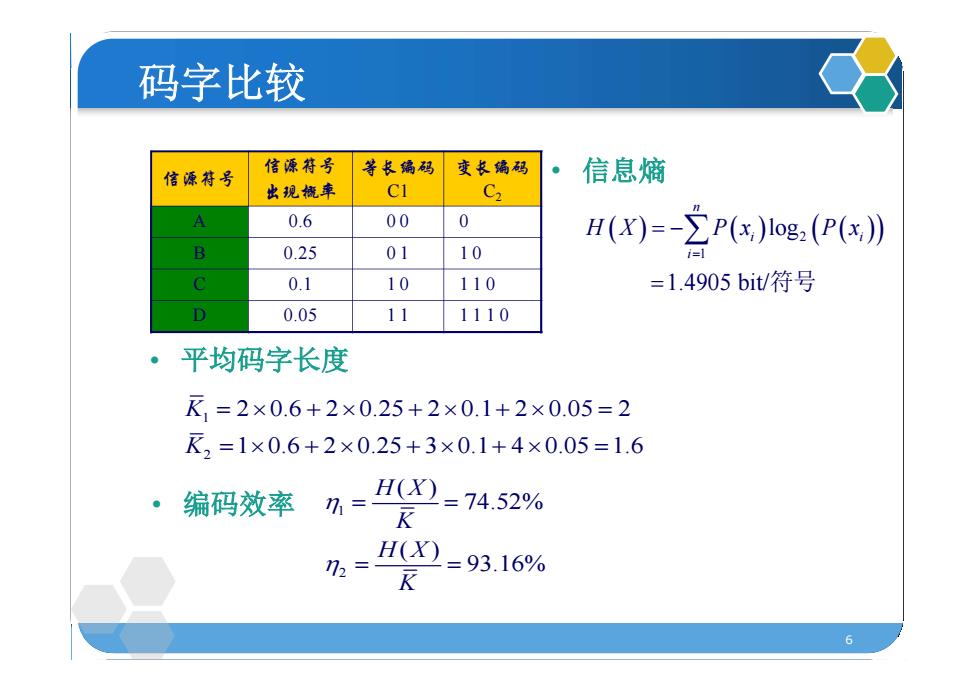
6 码字比较 信源符号 信源符号 出现概率 等长编码 C1 变长编码 C2 A 0.6 0 0 0 B 0.25 0 1 1 0 C 0.1 1 0 1 1 0 D 0.05 1 1 1 1 1 0 1 2 2 0.6 2 0.25 2 0.1 2 0.05 2 1 0.6 2 0.25 3 0.1 4 0.05 1.6 K K • 平均码字长度 • 信息熵 2 1 log 1.4905 bit/ n i i i H X P x P x 符号 • 编码效率 1 2 ( ) 74.52% ( ) 93.16% H X K H X K

变长编码 冬最佳编码: ■对于某一信源和某一码符号集来说,若有一唯一 可译码,其平均码长小于所有其他唯一可译码的 平均长度。 冬三种变长编码 香农(Shannon)编码 ■费诺(Fano)编码 ■哈夫曼(Huffma)编码
7 变长编码 v最佳编码: § 对于某一信源和某一码符号集来说,若有一唯一 可译码,其平均码长小于所有其他唯一可译码的 平均长度。 v三种变长编码 § 香农(Shannon)编码 § 费诺(Fano)编码 § 哈夫曼(Huffma)编码

香农编码 冬二进制香农码的编码步骤如下: 1.将信源符号按概率从大到小的顺序排列, p(a1)≥p(a2)≥.≥p(an) 2.确定满足下列不等式的整数K, -log2 p(ai)p(a.) k= 4.将P用二进制表示,并取小数点后K位作为符号a的编 码
8 v二进制香农码的编码步骤如下: 1.将信源符号按概率从大到小的顺序排列, p(a1)≥ p(a2)≥…≥ p(an) 2.确定满足下列不等式的整数Ki , -log2 p(ai)≤ Ki <1-log2 p(ai) 3.令p(a1)=0,用Pi 表示第i个码字的累加概率, 4.将Pi 用二进制表示,并取小数点后Ki 位作为符号ai 的编 码。 香农编码 1 1 ( ) i i k k P p a
香农编码 ·例:有一单符号离散无记忆信源 x X2 X3 X4 X5 0.40.30.20.050.05 对该信源进行二进制香农编码,其过程如表所示: 信源符号 累加 码 以i=3为例 符号 機率 機率 -log p(x 长 码字长度: 码字 K3=[l0g0.2]=3 X P(xi) P K 累加视Q X 0.4 0 1.32 2 00 =0ζ9-9 .10110. X2 0.3 0.4 1.73 2 01 X3 0.2 0.7 2.32 3 101 101 11100 X4 0.05 0.9 4.3 5 11100 X5 0.05 0.95 这些码字没有占满所有树叶, 11110 所以不是最佳变长编码
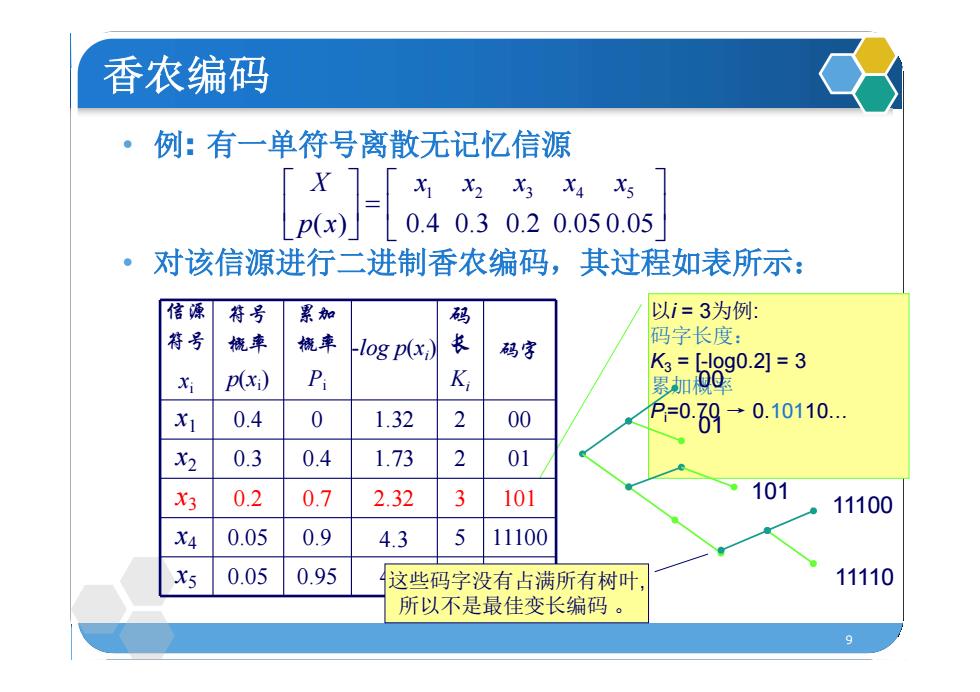
9 • 例: 有一单符号离散无记忆信源 • 对该信源进行二进制香农编码,其过程如表所示: 以i = 3为例: 码字长度: K3 = [-log0.2] = 3 累加概率 Pi=0.70 → 0.10110… 00 01 101 11100 11110 信源 符号 xi 符号 概率 p(xi) 累加 概率 Pi -log p(xi) 码 长 Ki 码字 x1 0.4 0 1.32 2 00 x2 0.3 0.4 1.73 2 01 x3 0.2 0.7 2.32 3 101 x4 0.05 0.9 4.3 5 11100 x5 0.05 0.95 4.3 5 11110 1 2 3 4 5 ( ) 0.4 0.3 0.2 0.05 0.05 X x x x x x p x 香农编码 这些码字没有占满所有树叶, 所以不是最佳变长编码

香农编码 ·平均码长: K=∑px)K,=0.4x2+0.3×2+0.2×3+0.05x5x2=2.5 i=1 ·信源熵: H(X)=-0.4log0.4-0.3log0.3-0.2log0.2-2×0.05l0g0.05 =1.95 ·编码效率 H(X)1.95 =78% 2.5 10
10 • 平均码长: 5 1 ( ) 0.4 2 0.3 2 0.2 3 0.05 5 2 2.5 i i i K p x K • 信源熵: ( ) 0.4log0.4 0.3log0.3 0.2log0.2 2 0.05log0.05 1.95 H X • 编码效率 ( ) 1.95 78% 2.5 H X K 香农编码