
厚德 求真 砺学 笃行 西安子科技大学 XIDIAN UNIVERSITY 毫米波雷达综合实验 第3讲毫米波雷达测距原理及实验

目录TENTS 02 图书能 测距原理介绍 测距实验讲解 厚糖求真砺学笃行 XIDIAN UNIVERSITY
2 目 录

PART 01 测距原理介绍

01 测距原理介绍一线性调频连续波测距 历安毛子代技大学 >本模块主要解决以下几个问题 雷达如何估算它与位于雷达前方的物体之间的距离? 如果有多个物体,并且它们与雷达之间的距离是不同的,将会怎样? ·两个物体能够相距多近而仍然能够被解析为两个物体? ·什么决定雷达可以看到的最远距离? 厚德求真丽学笃行 XIDIAN UNIVERSITY
4 01 测距原理介绍—线性调频连续波测距 ➢本模块主要解决以下几个问题: • 雷达如何估算它与位于雷达前方的物体之间的距离? • 如果有多个物体,并且它们与雷达之间的距离是不同的,将会怎样? • 两个物体能够相距多近而仍然能够被解析为两个物体? • 什么决定雷达可以看到的最远距离?
01 测距原理介绍一传统雷达脉冲波测距 从雷达回波提取的目标距离信息 Total T-2g Radar Transmitted RF Pulse Target 普通脉冲雷达,通过测量发射信号传 播到目标并返回来的时间来测定目标 的距离 R (a) Backscattered RF Pulse Radar Target (b) R=C·T/2(其中c为光速,T为延迟时间) 基于窄脉冲的测距方法,脉冲越窄,测距精度越高。但是在峰值功率受限的 情况下,发射窄脉冲辐射的能量有限 厚随取真丽学笃行 XIDIAN UNIVERSITY
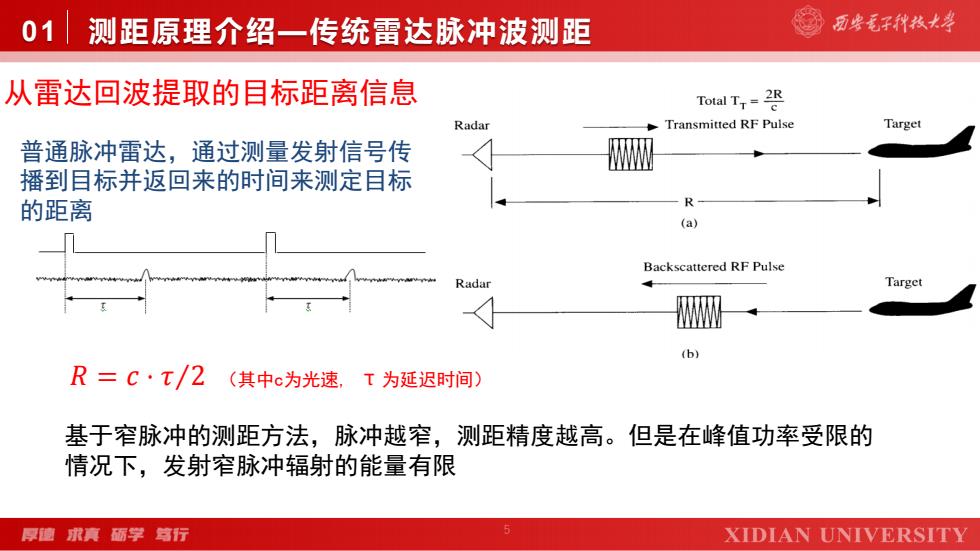
5 01 测距原理介绍—传统雷达脉冲波测距 从雷达回波提取的目标距离信息 普通脉冲雷达,通过测量发射信号传 播到目标并返回来的时间来测定目标 的距离 (其中c为光速, τ为延迟时间) 基于窄脉冲的测距方法,脉冲越窄,测距精度越高。但是在峰值功率受限的 情况下,发射窄脉冲辐射的能量有限 𝑅 = 𝑐 ⋅ 𝜏Τ2

01测距原理介绍一匹配滤波 历安毛子代技大势 使滤波器输出信噪比在某一特定时刻达到最大一匹配滤波器 匹配滤波器(match filter)是最佳线性滤波器 x(t)=s(t)+n(t) 匹配滤波器 y(t)=so(t)+no(t) 的一种,该滤波器的准则是输出信噪比最大,常 H() 用于通信、雷达等系统的接收机中。 s(t):信号 n(t):噪声 时域匹配滤波 频城匹配滤波 根据h()=s(-)可构造时域匹配滤波器为发射信号 将发射脉冲信号进行「FT,再取共轭,与信号 时间反褶再取共轭,再与发射信号进行线性卷积即可 的FFT在频域相乘,最后IFF变换回时域。 实现脉冲压缩。 H(f)=s(f) S(f=s(H() s(t)=S(t)×s(-t) so(t)=IFFT[S(f)H(f)] IFFT FFT(s(t).FFT(h(t) 厚德求真丽学笃行 XIDIAN UNIVERSITY
6 01 测距原理介绍—匹配滤波 匹配滤波器(match filter)是最佳线性滤波器 的一种,该滤波器的准则是输出信噪比最大,常 用于通信、雷达等系统的接收机中。 使滤波器输出信噪比在某一特定时刻达到最大——匹配滤波器 匹配滤波器 H(ω) x(t)=s(t)+n(t) y(t)=s0(t)+n0(t) s(t):信号 n(t):噪声 时域匹配滤波 根据 可构造时域匹配滤波器为发射信号 时间反褶再取共轭,再与发射信号进行线性卷积即可 实现脉冲压缩。 频域匹配滤波 将发射脉冲信号进行FFT,再取共轭,与信号 的FFT在频域相乘,最后IFFT变换回时域。 * h t s t ( ) ( ) = − * 0 s t s t s t ( ) ( ) ( ) = − 0 S f S f H f ( ) ( ) ( ) = * H f S f ( ) ( ) = 𝑠0 𝑡 = 𝐼𝐹𝐹𝑇 𝑆(𝑓ሻ𝐻(𝑓ሻ = 𝐼𝐹𝐹𝑇 𝐹𝐹𝑇 𝑠(𝑡ሻ ⋅ 𝐹𝐹𝑇(ℎ(𝑡ሻ൯
01 测距原理介绍一匹配滤波 进入匹配波之前的信号 匹配滤波后输出 10 0.5 20 50 1000 2000 3000 ·从幅频特性来看,匹配滤波器和输入信号的幅频特性完全一样。这也就是说,在信号越强的频 率点,滤波器的放大倍数也越大;在信号越弱的频率点,滤波器的放大倍数也越小。也就是说, 匹配滤波器是让信号尽可能通过,而不管噪声的特性 。 从相频特性上看,匹配滤波器的相频特性和输入信号正好完全相反。这样,通过匹配滤波器后, 信号的相位为0,正好能实现信号时域上的相干叠加。而噪声的相位是随机的,只能实现非相 干叠加。这样在时域上保证了输出信噪比的最大。 匹配滤波器无论是从时域还是从频域,都充分保证了信号尽可能大地通过,噪声尽可能小地通 过,因此能获得最大信噪比的输出。 厚德R真肠学笃行 XIDIAN UNIVERSITY
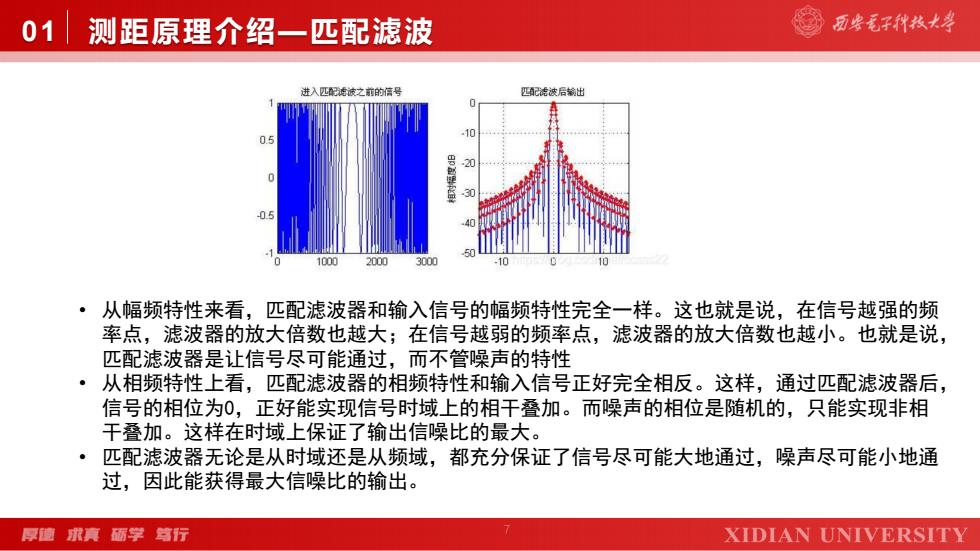
7 01 测距原理介绍—匹配滤波 • 从幅频特性来看,匹配滤波器和输入信号的幅频特性完全一样。这也就是说,在信号越强的频 率点,滤波器的放大倍数也越大;在信号越弱的频率点,滤波器的放大倍数也越小。也就是说, 匹配滤波器是让信号尽可能通过,而不管噪声的特性 • 从相频特性上看,匹配滤波器的相频特性和输入信号正好完全相反。这样,通过匹配滤波器后, 信号的相位为0,正好能实现信号时域上的相干叠加。而噪声的相位是随机的,只能实现非相 干叠加。这样在时域上保证了输出信噪比的最大。 • 匹配滤波器无论是从时域还是从频域,都充分保证了信号尽可能大地通过,噪声尽可能小地通 过,因此能获得最大信噪比的输出
01 测距原理介绍一线性调频连续波测距 历安毛子代技大势 什么是线性调频脉冲? 调频连续波雷达发射一种称为“chirp”的信号。一个 “chirp'”是频率随时间线性增加的正弦曲线,左图中所 示,是振幅与时间的关系图。 “chirp'”信号的特征也可以用“f-t图”来表示。 。 “chirp"”的三个重要参数是起始频率(fc),带宽(B)和 持续时间(Tc)。 B=4GHz ·“chirp'”的斜率定义了“chirp'”上升的速率。在 在这个例子中,“chirp”扫过40us中的4GHz带宽 对应于100MHz/us的斜率 T.=40us 厚求真丽学笃行 XIDIAN UNIVERSITY
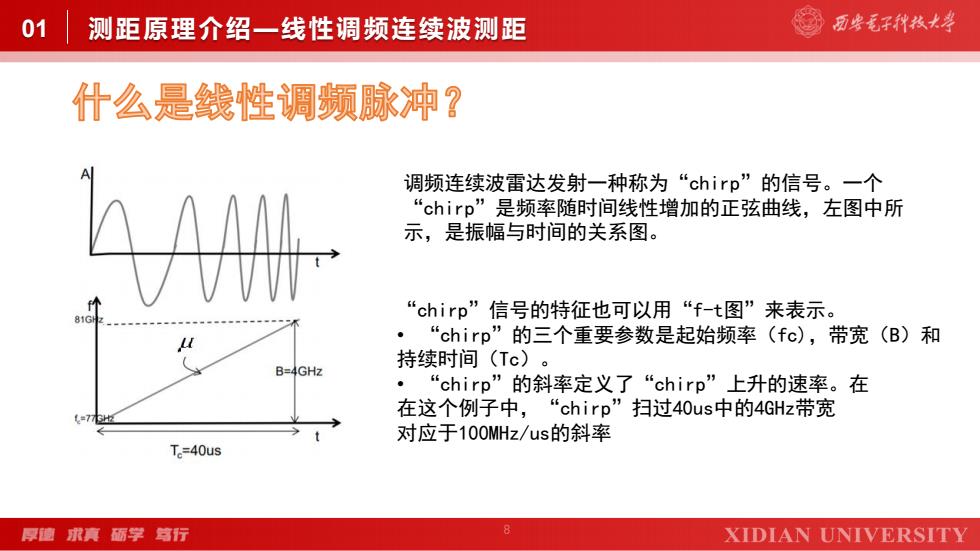
8 01 测距原理介绍—线性调频连续波测距 调频连续波雷达发射一种称为“chirp”的信号。一个 “chirp”是频率随时间线性增加的正弦曲线,左图中所 示,是振幅与时间的关系图。 “chirp”信号的特征也可以用“f-t图”来表示。 • “chirp”的三个重要参数是起始频率(fc),带宽(B)和 持续时间(Tc)。 • “chirp”的斜率定义了“chirp”上升的速率。在 在这个例子中,“chirp”扫过40us中的4GHz带宽 对应于100MHz/us的斜率

01 测距原理介绍一线性调频连续波测距 历安毛子代技大男 ② TX ant 简化的FMCW雷达框图 1、合成器(synth)产生chirp。 Synth 2、chirpl由发射天线发射。 RX ant mixer IF signal 3、chirp,从物体反射回来,反射回来的chirp被接收天线接收。 4、接收信号和发送信号通过“混合”,产生“中频信号”。 混频器示意图 x=sin(ot+) x2 =sin(@2t+2) Xout xa=sin[(o,-o2)t+(4-4)] 厚德R真丽学等行 XIDIAN UNIVERSITY
9 01 测距原理介绍—线性调频连续波测距 ( ) ( ) ( ) ( ) 1 1 1 2 2 2 1 2 1 2 sin sin out sin x t x t x t = + = + = − + − 简化的FMCW 雷达框图 1、合成器(synth)产生chirp。 2、chirp由发射天线发射。 3、chirp从物体反射回来,反射回来的chirp被接收天线接收。 4、接收信号和发送信号通过“混合”,产生 “中频信号”。 混频器示意图

01 测距原理介绍一线性调频连续波测距 历安毛子代技大势 为什么要使用混频器? TX chirp 左图显示了从物体反射的发射信号和接收信号。而接收信号只是发射 4--RX chirp 信号的延迟版本。(τ表示从雷达到物体然后又返回的时间延迟) ·混频器输出处的信号频率是TX chirpi和RX chirpl的瞬时频率差。如 左下图所示,这是一条直线。 ·因此,雷达前方的单个目标会产生一个频率恒定的中频信号。 f +--IF signal -这个音调的频率是μT=μ召(因为T=召,其中d是物体 的距离,c是光速) 厚随求真丽学笃行 10 XIDIAN UNIVERSITY
10 01 测距原理介绍—线性调频连续波测距 左图显示了从物体反射的发射信号和接收信号。而接收信号只是发射 信号的延迟版本。(τ表示从雷达到物体然后又返回的时间延迟) • 混频器输出处的信号频率是TX chirp和RX chirp的瞬时频率差。如 左下图所示,这是一条直线。 • 因此,雷达前方的单个目标会产生一个频率恒定的中频信号。 –这个音调的频率是μτ=μ 2d c (因为τ= 2d c ,其中d是物体 的距离,c是光速)