
第六章量子机器学习
第六章 量子机器学习

6.1量子K-means算法 聚类算法是无监督学习算法中较为重要的一类。以 最普遍使用的k-means算法为例,该算法以距离的远 近作为样本相似性指标,即两个样本的距离越近相似 程度就越高。当遇到海量样本数据时,k-means算法存 在时间开销较大的缺点
6.1 量子 K-means 算法 聚类算法是无监督学习算法中较为重要的一类。以 最普遍使用的 k-means 算法为例,该算法以距离的远 近作为样本相似性指标,即两个样本的距离越近相似 程度就越高。当遇到海量样本数据时,k-means 算法存 在时间开销较大的缺点

Lloyd等人于2013年提出了量子版最近中心算法。量子 最近中心算法可视为经典k-means聚类算法的子过程, 使用该方法可对经典算法进行指数级提速。 Quantum algorithms for supervised and unsupervised machine learning Seth Lloyd,3,Masoud Mohseni2,Patrick Rebentrost 1.Massachusetts Institute of Technology,Research Laboratory for Electronics 2.Google Research 3.To whom correspondence should be addressed:slloyd@mit.edu
Lloyd 等人于 2013 年提出了量子版最近中心算法 。量子 最近中心算法可视为经典 k-means 聚类算法的子过程, 使用该方法可对经典算法进行指数级提速

量子最近中心算法的核心思想是对实向量间的距离作 比较,通过寻找向量u与集合{v}中的哪个量的距 离最近,从而不断分类,进而不断自动获得聚类结果, argminu-m'·∑v
量子最近中心算法的核心思想是对实向量间的距离作 比较,通过寻找向量 u 与集合 {v} 中的哪个量的距 离最近,从而不断分类,进而不断自动获得聚类结果

步骤 (1)将实向量u=(4o,41,,4n) 转换成量子 态W〉,从而将向量的距离比较转换成量子态间 的距离比较。 )= u
步骤 (1)将实向量 转换成量子 态 ,从而将向量的距离比较转换成量子态间 的距离比较

(2)定义纠缠态p〉和p) 时-方0+2 =方o后2n 为归一化系数 |〉为c簇的第j个向量,m为样本总数
(2)定义纠缠态 和 为归一化系数 为 c 簇的第 j 个向量,m 为样本总数
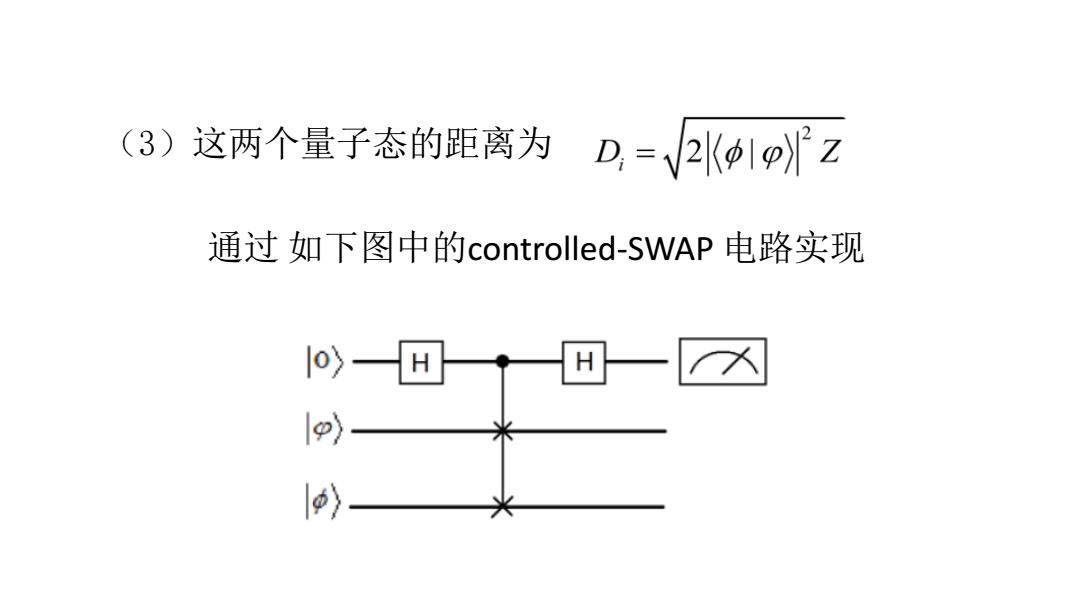
(3)这两个量子态的距离为D,=V2K1z 通过如下图中的controlled-SWAP电路实现 〉 〉
(3)这两个量子态的距离为 通过 如下图中的controlled-SWAP 电路实现
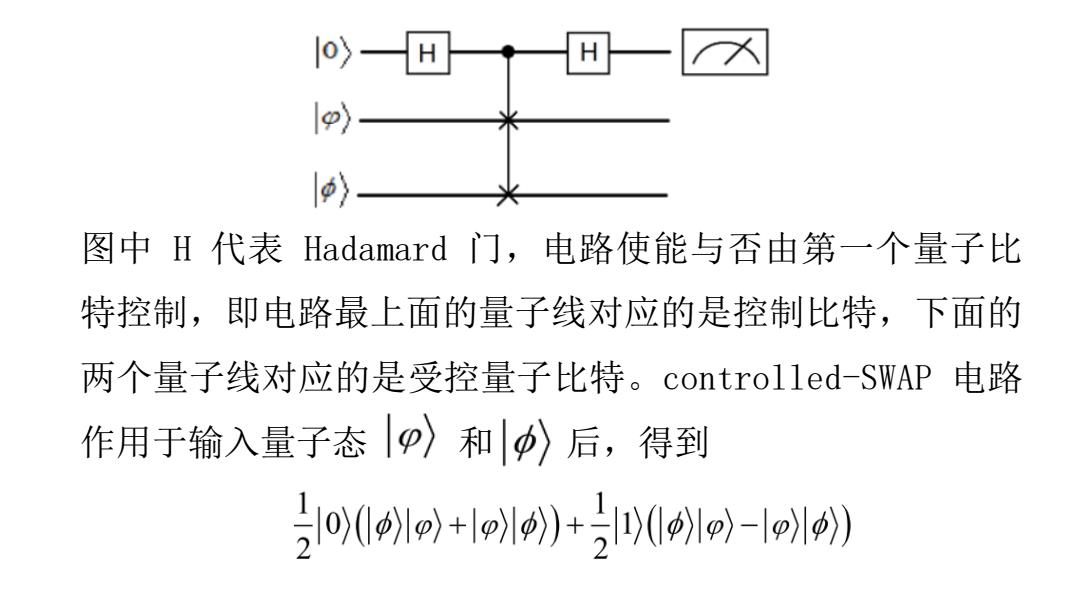
1o>- 入 1) 1〉 图中H代表Hadamard门,电路使能与否由第一个量子比 特控制,即电路最上面的量子线对应的是控制比特,下面的 两个量子线对应的是受控量子比特。controlled-SWAP电路 作用于输入量子态p〉和p〉后,得到 21o1++l(o-》
图中 H 代表 Hadamard 门,电路使能与否由第一个量子比 特控制,即电路最上面的量子线对应的是控制比特,下面的 两个量子线对应的是受控量子比特。controlled-SWAP 电路 作用于输入量子态 和 后,得到

对第一位量子比特进行测量,得0的概率为 p(+2K1 则 K1p)=2P(Io)-1
对第一位量子比特进行测量,得 0 的概率为 则

k-means算法中初始点的选择十分重要,好的初始点将极大 地缩短迭代次数。初始点选择的是否足够好,评判的一个标 准是,需要尽可能将初始点稀疏分布于整个样本空间中,即 各点之间距离尽可能大。为了优化初始点,Ioyd使用量子 绝热演化算法来实现k-means-++算法最优初始点的选择。其 基本思想为,首先初始化Hamiltonian量
k-means 算法中初始点的选择十分重要,好的初始点将极大 地缩短迭代次数。初始点选择的是否足够好,评判的一个标 准是,需要尽可能将初始点稀疏分布于整个样本空间中,即 各点之间距离尽可能大。为了优化初始点,Lloyd 使用量子 绝热演化算法来实现 k-means++算法最优初始点的选择。其 基本思想为,首先初始化 Hamiltonian 量