
第5章:回朔法 Backtracking Algorithm)
第5章:回朔法 ( Backtracking Algorithm)

知识要点 3掌握用回溯法解题的算法框架 Φ子集树算法框架 Φ排列树算法框架 ?了解NP完全问题 ΦNP完全问题的定义和研究意义 ?通过应用范例学习回溯法的设计策略 Φ0/1背包问题;旅行商问题(TSP);最优装载问题 Φ批收处理作业调度;连续邮资问题;圆排列问题 ΦN-皇后问题;最大团问题;图的m着色问题
知识要点 掌握用回溯法解题的算法框架 子集树算法框架 排列树算法框架 了解NP完全问题 NP完全问题的定义和研究意义 通过应用范例学习回溯法的设计策略 0/1背包问题;旅行商问题(TSP);最优装载问题 批处理作业调度;连续邮资问题;圆排列问题 N-皇后问题;最大团问题;图的m着色问题

5.1回溯法算法框架 Backtracking Algorithm Paradigm
5.1 回溯法算法框架 ( Backtracking Algorithm Paradigm )
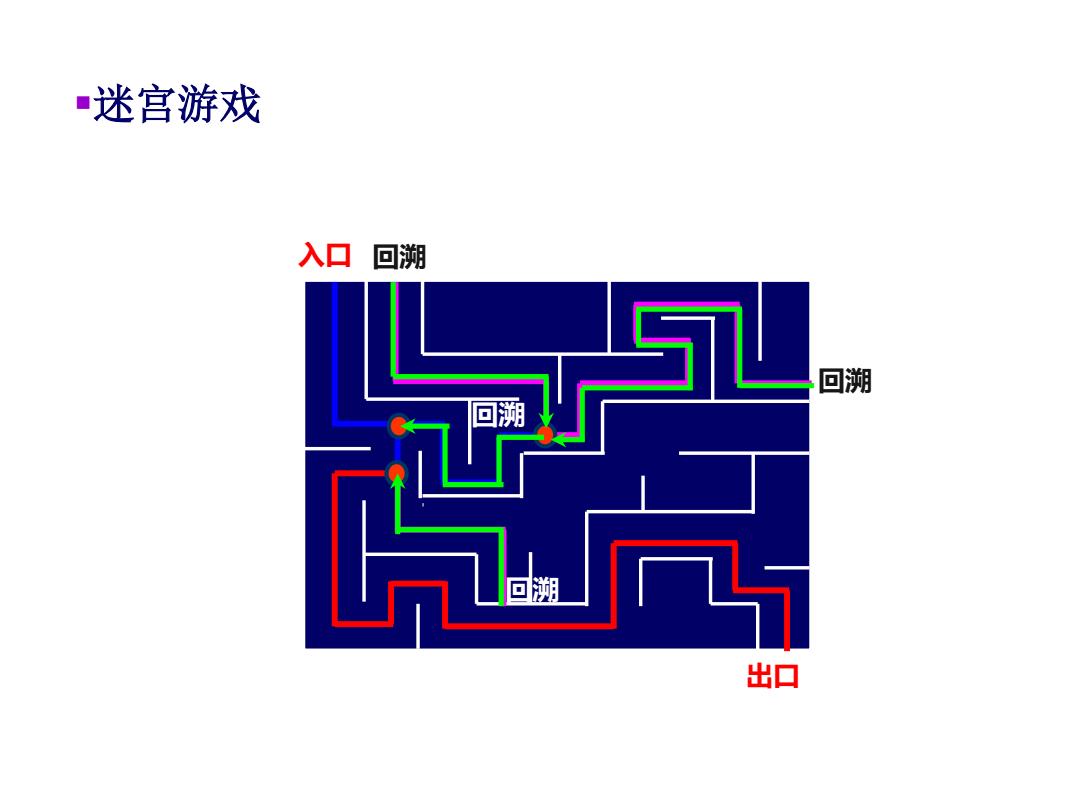
·迷宫游戏 入口回溯 与 回溯 出口
回溯 回溯 入口 出口 回溯 ▪迷宫游戏 回溯

搜索算法 >对某些问题建立数学模型时,即使有一定的数学 模型,但采用数学方法解决有一定的困难。对于这 一 类试题,我们用模拟或搜索求解。 >在缺乏解决问题的有效模型时,搜索却是一种行 之有效的解决问题的基本方法。 枚举法(穷举法) 深度优先搜索(回溯法) 广度优先搜索
搜索算法 ➢对某些问题建立数学模型时,即使有一定的数学 模型,但采用数学方法解决有一定的困难。对于这 一类试题,我们用模拟或搜索求解。 ➢在缺乏解决问题的有效模型时,搜索却是一种行 之有效的解决问题的基本方法。 枚举法(穷举法) 深度优先搜索(回溯法) 广度优先搜索

回溯法的基本概念 回溯法是一种选优搜索法(试探法),被称为通用的解题方法 3 基本思想:将n元问题P的状态空间E表示成一棵高为n的带权有序 树T,把在E中求问题P的解转化为在T中搜索问题P的解 3 解题方法:按选优条件对T进行深度优先搜索,以达到目标 从根结点出发深度优先搜索解空间树 当探索到某一结点时,要先判断该结点是否包含问题的解 如果包含,就从该结点出发继续按深度优先策略搜索 否则逐层向其祖先结点回溯(退回一步重新选择) 满足回溯条件的某个状态的点称为“回溯点” 算法结束条件: 求所有解:回溯到根,且根的所有子树均已搜索完成 求任一解:只要搜索到问题的一个解就可以结束
回溯法的基本概念 回溯法是一种选优搜索法(试探法),被称为通用的解题方法 基本思想:将n元问题P的状态空间E表示成一棵高为n的带权有序 树T,把在E中求问题P的解转化为在T中搜索问题P的解 解题方法:按选优条件对T进行深度优先搜索,以达到目标 从根结点出发深度优先搜索解空间树 当探索到某一结点时,要先判断该结点是否包含问题的解 ━ 如果包含,就从该结点出发继续按深度优先策略搜索 ━ 否则逐层向其祖先结点回溯(退回一步重新选择) ━ 满足回溯条件的某个状态的点称为“回溯点” 算法结束条件: ━ 求所有解:回溯到根,且根的所有子树均已搜索完成 ━ 求任一解:只要搜索到问题的一个解就可以结束
问题的解空间 @R 应用回法解题时,首先应明确问题的解空间 Φ问题的解空间应至少包含该问题的一个(最优)解 例如:对于有种备选物品的0/1背包问题而言 解空间可以由长度为n的向量来表示 显然:该解空间包含了对该问题所有可能的解法 @8 定义了问题的解空间后,可以将其组织成树或图的形式 Φ例如:=3的0/1背包问题,解空间可用一棵完全二叉树表示 。从根到任一叶结点的路径表示解空间的一个元素
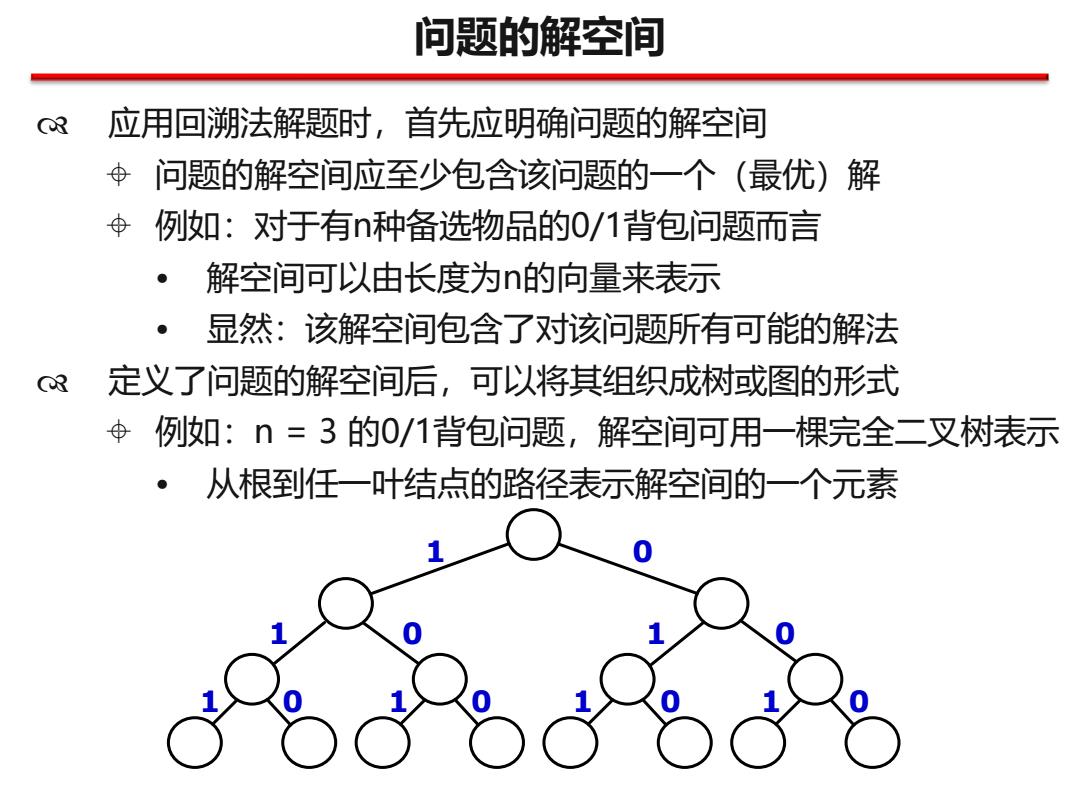
问题的解空间 应用回溯法解题时,首先应明确问题的解空间 问题的解空间应至少包含该问题的一个(最优)解 例如:对于有n种备选物品的0/1背包问题而言 • 解空间可以由长度为n的向量来表示 • 显然:该解空间包含了对该问题所有可能的解法 定义了问题的解空间后,可以将其组织成树或图的形式 例如:n = 3 的0/1背包问题,解空间可用一棵完全二叉树表示 • 从根到任一叶结点的路径表示解空间的一个元素 1 0 1 0 1 0 1 0 1 0 1 0 1 0

生成问题状态的基本方法 @R 基本概念 Φ扩展结点:一个正在产生子结点的结点称为扩展结点 Φ活结点:一个自身已生成但其子结点尚未全部生成的结点 Φ死结点:一个所有子结点已经产生的结点称做死结点 8 深度优先的问题状态生成法 Φ对一个扩展结点R,一旦产生了它的一个子结点C 则将其作为新扩展结点,并对以C为根的子树进行穷尽搜索 在完成对子树C的穷尽搜索后,将R重新变成扩展结点 继续生成R的下一个子结点,若存在,则对其进行穷尽搜索 3 宽度优先的问题状态生成法 Φ在一个扩展结点变成死结点之前,它一直是扩展结点
生成问题状态的基本方法 基本概念 扩展结点:一个正在产生子结点的结点称为扩展结点 活结点:一个自身已生成但其子结点尚未全部生成的结点 死结点:一个所有子结点已经产生的结点称做死结点 深度优先的问题状态生成法 对一个扩展结点R,一旦产生了它的一个子结点C ⚫ 则将其作为新扩展结点,并对以C为根的子树进行穷尽搜索 ⚫ 在完成对子树C的穷尽搜索后,将R重新变成扩展结点 ⚫ 继续生成R的下一个子结点,若存在,则对其进行穷尽搜索 宽度优先的问题状态生成法 在一个扩展结点变成死结点之前,它一直是扩展结点

回溯法的解题思路 3 针对所给问题,定义问题的解空间 R 确定易于搜索的解空间结构 3 从根结点开始深度优先搜索解空间(利用剪枝避免无效搜索) 此时:根结点成为活结点,并成为当前的扩展结点 Φ进一步的搜索从当前扩展结点开始 向纵深方向移至一个新结点 该新结点成为新的活结点,并成为当前扩展结点 若在当前扩展结点处不能再向纵深方向移动 则当前扩展结点变为死结点 此时应回溯至最近的活结点,将其作为当前扩展结点 3 回溯法以这种方式递归地在解空间中搜索 Φ直至找到所要求的解,或者解空间中已经没有活结点为止
回溯法的解题思路 针对所给问题,定义问题的解空间 确定易于搜索的解空间结构 从根结点开始深度优先搜索解空间(利用剪枝避免无效搜索) 此时:根结点成为活结点,并成为当前的扩展结点 进一步的搜索从当前扩展结点开始 ⚫ 向纵深方向移至一个新结点 ⚫ 该新结点成为新的活结点,并成为当前扩展结点 若在当前扩展结点处不能再向纵深方向移动 ⚫ 则当前扩展结点变为死结点 ⚫ 此时应回溯至最近的活结点,将其作为当前扩展结点 回溯法以这种方式递归地在解空间中搜索 直至找到所要求的解,或者解空间中已经没有活结点为止

递割归回溯:通用算法框架 @R 回溯法对解空间作深度优先搜索 Φ 因此在一般情况下用递归方法实现回溯法 void backtrack (int t){ t表示递归深度 if (t n){ 即当前扩展结点在解空间树中的深度 output(x); n用来控制递归深度 表的高黠点 Output(x) else 对可行解进行处理:记录或输出 for (int i f(n,t);i<=g(n,t);i++)
递归回溯:通用算法框架 回溯法对解空间作深度优先搜索 因此在一般情况下用递归方法实现回溯法 void backtrack (int t) { if (t > n){ output(x); } else{ for (int i = f(n, t); i n 表示已搜索到一个叶结点 Output(x) 对可行解进行处理:记录或输出