
例 9 6.5RSA公钥密码
6.5 RSA公钥密码
RSA 好 RSA算法描述 RSA的快速模指数运算 RSA的安全性
RSA RSA算法描述 RSA的安全性 RSA的快速模指数运算

RSA算法描述 ●RSA公钥密码体制历史 麻省理工学院Ron Rivest、.Adi Shamiri和Leonard Adleman于1978年一起提出RSA加密算法
RSA算法描述 RSA公钥密码体制历史 麻省理工学院Ron Rivest、Adi Shamir和Leonard Adleman于1978年一起提出RSA加密算法

RSA算法描述 ·算法描述—密钥生成 ■选取两互异大素数p和q ■计算=p×q和其欧拉函数值p(n)=(p一1)(q一1) ■选一整数e,1<ep(m),使得gcd(mn),e)=1 ■在模on)下,计算e的逆元d.即求d,使得 ed=1 mod o(n) ■(e,m为公钥,d为私钥
RSA算法描述 算法描述——密钥生成 选取两互异大素数p和q 计算 n=p×q 和其欧拉函数值(n)=(p-1)(q-1) 选一整数e,1 < e<(n),使得 gcd((n), e)=1 在模(n)下,计算e的逆元d. 即求d, 使得 𝒆 𝒅≡ 1 mod (n) (e, n)为公钥,d为私钥
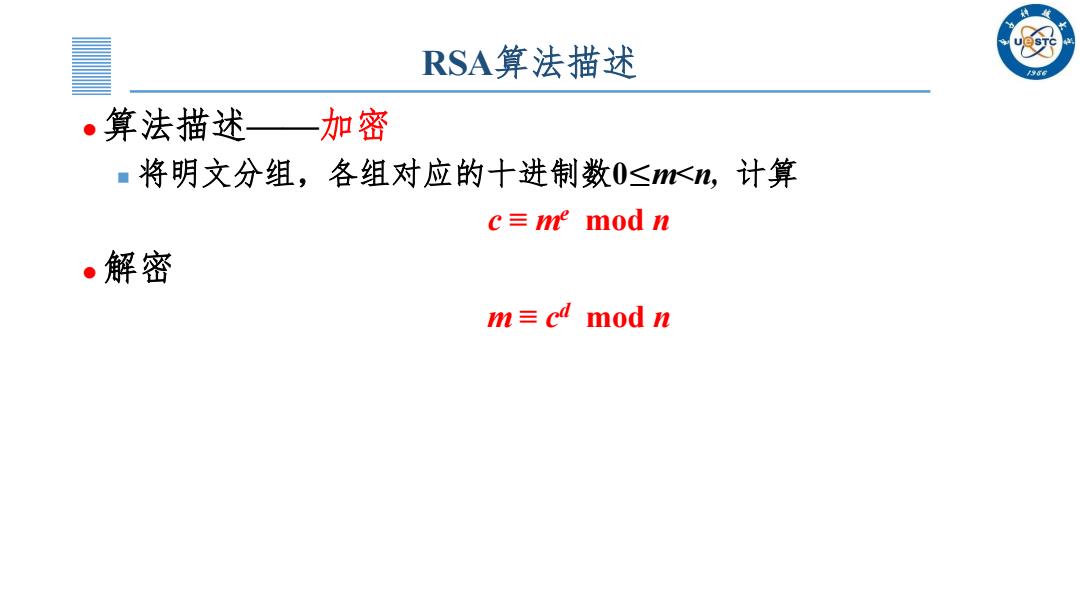
RSA算法描述 。算法描述一加密 ■将明文分组,各组对应的十进制数0≤<n,计算 c三ne mod n 。解密 m≡c4modn
RSA算法描述 算法描述——加密 将明文分组,各组对应的十进制数0≤m<n, 计算 c ≡ me mod n 解密 m ≡ c d mod n

RSA算法描述 。RSA解密过程的正确性 ■由加密过程知c≡ne mod n,又de三1modp(n),故 cd mod n≡ned mod n≡ml+rgm)mod n ■分两种情况 ①gcd(m,n)=1,则由Euler定理得 m9m≡1modn,mom≡1modn, ml+rom≡n mod n cd mod n=m
RSA算法描述 RSA解密过程的正确性 由加密过程知c ≡ me mod n ,又de ≡ 1 mod 𝝋(𝒏) ,故 c d mod n≡med mod n ≡m1+r(n) mod n 分两种情况 ①gcd(m, n)=1 ,则由Euler定理得 m(n) ≡1 mod n, mr(n) ≡1 mod n, m1+r(n) ≡m mod n c d mod n≡m

RSA算法描述 ②gcd(m,n)≠1 不妨设gcd(m,m)=p,m=p, 由gcd(m,q)=1及Euler定理得mmg≡1modq,所以 mq)≡1m0dq, [moqp)≡1m0d4, rW≡1modq 因此存在一整数b,使得m四=1+bg,两边同乘以m得 ml+ram)=m+bqm-m+bqxp=m+xbn 即ml+rg)≡n mod n,所以cd mod n=m
RSA算法描述 由gcd(m, q)=1及Euler定理得m(q) ≡1 mod q,所以 mr(q) ≡1 mod q, [mr(q) ] (p) ≡1 mod q, mr(n) ≡1 mod q 因此存在一整数b,使得mr(n) =1+bq,两边同乘以m得 m1+r(n) =m+bqm=m+bqxp=m+xbn 即m1+r(n) ≡m mod n,所以c d mod n≡m ② gcd(m,n)≠1 不妨设gcd(m, n)=p, m=xp

RSA算法描述 。举例 ■密钥生成: 设p=7,=17.n=p×q=119,pm)=(p-1)(q-1)=96。取=5,计算私钥 d=77 ■加密:设明文=4, c=45m0d119=72 ■解密: 7277m0d119≡4
RSA算法描述 举例 密钥生成: 设p=7, q=17. n=p×q=119, (n) =(p-1)(q-1)=96。取e=5,计算私钥 d=77 加密:设明文m=4, c≡45 mod 119≡72 解密: 7277 mod 119≡4

RSA的快速模指数运算 。依次模乘运算 ■RSA加密和解密算法都涉及到模指数运算,ne mod ni和cd mod n 两个操作。 ■对模指数运算最直接的方法是依次做模乘运算。为计算ne mod n 执行: m×m×…×m e ■这种方法效率很低,需要计算-1次模乘法运算
RSA的快速模指数运算 依次模乘运算 RSA加密和解密算法都涉及到模指数运算,me mod n和c d mod n 两个操作。 对模指数运算最直接的方法是依次做模乘运算。为计算me mod n 执行: 这种方法效率很低,需要计算e-1次模乘法运算。 e m m m

RSA的快速模指数运算 。平方-乘运算 ■求x16,直接计算的话需做15次乘法。然而如果重复对每个部分结 果做平方运算即求x,x2,x4,x8,x16则只需4次乘法
RSA的快速模指数运算 平方-乘运算 求x 16 ,直接计算的话需做15次乘法。然而如果重复对每个部分结 果做平方运算即求x,x 2 ,x 4 ,x 8 ,x 16则只需4次乘法