
第3章:动态规划 Dynamic Programming
第3章:动态规划 Dynamic Programming

知识要点 3理解动态规划算法的概念 ?掌握动态规划算法的基本要素 Φ最优子结构性质 Φ重叠子问题性质 ?掌握动态规划算法的设计方法 Φ找出最优解的性质,并刻划其结构特征 Φ递归地定义最优值 Φ以自底向上的方式计算出最优值 Φ根据计算最优值时得到的信息,构造最优解
知识要点 理解动态规划算法的概念 掌握动态规划算法的基本要素 最优子结构性质 重叠子问题性质 掌握动态规划算法的设计方法 找出最优解的性质,并刻划其结构特征 递归地定义最优值 以自底向上的方式计算出最优值 根据计算最优值时得到的信息,构造最优解

知识要点 ?通过应用范例学习动态规划算法设计策略 Φ矩阵连乘问题 Φ最长公共子序列问题 Φ最大子段和问题 Φ凸多边形最优三角剖分问题 Φ图像压缩问题 Φ0-1背包问题
知识要点 通过应用范例学习动态规划算法设计策略 矩阵连乘问题 最长公共子序列问题 最大子段和问题 凸多边形最优三角剖分问题 图像压缩问题 0-1背包问题
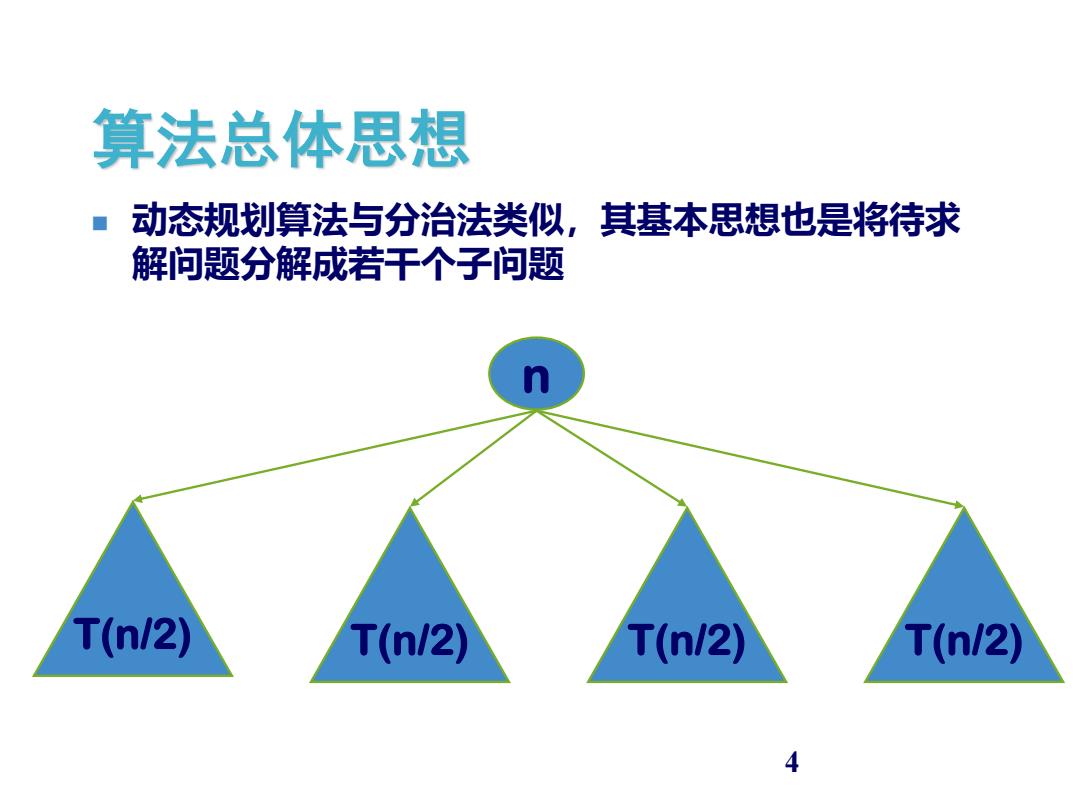
算法总体思想 ■ 动态规划算法与分治法类似,其基本思想也是将待求 解问题分解成若干个子问题 T(n/2) T(n/2) T(n/2) T(n/2) 4
4 ◼ 动态规划算法与分治法类似,其基本思想也是将待求 解问题分解成若干个子问题 算法总体思想 n T(n/2) T(n/2) T(n/2) T(n/2)
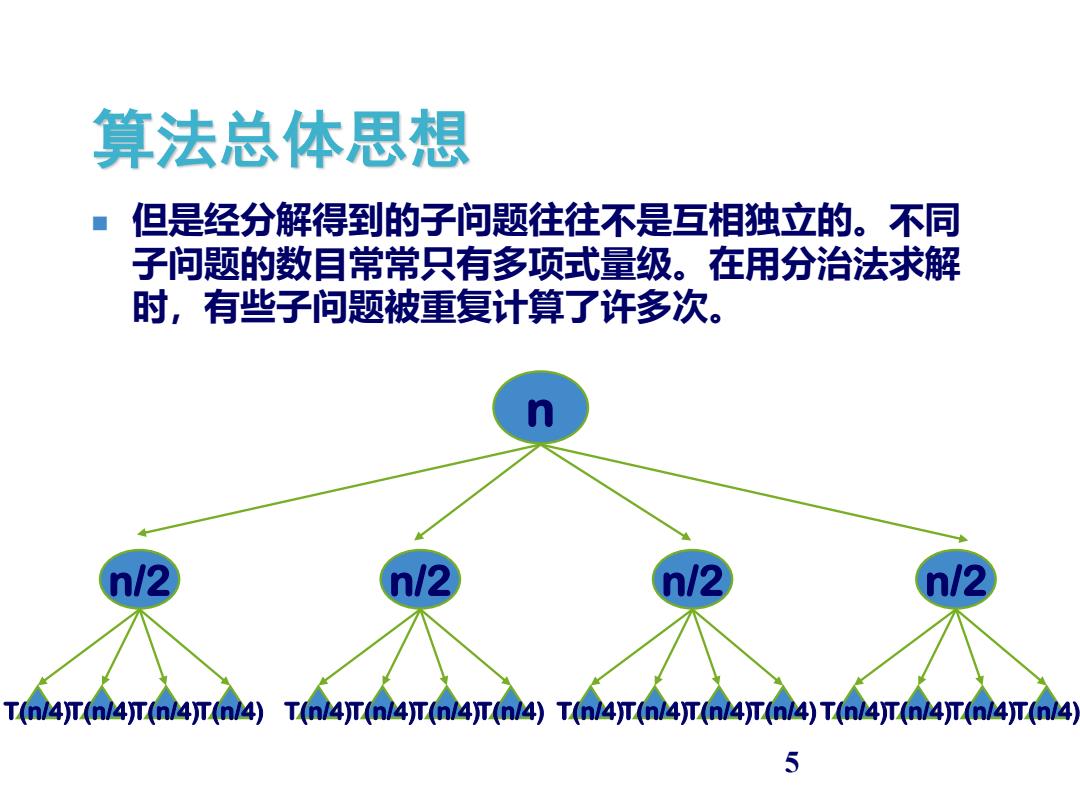
算法总体思想 但是经分解得到的子问题往往不是互相独立的。不同 子问题的数目常常只有多项式量级。在用分治法求解 时,有些子问题被重复计算了许多次。 n/2 n12 n/2 n/2 T64T64T64T614)T4T4T14T04)T14T4T4T4)T14T14T4T4) 5
5 ◼ 但是经分解得到的子问题往往不是互相独立的。不同 子问题的数目常常只有多项式量级。在用分治法求解 时,有些子问题被重复计算了许多次。 算法总体思想 n n/2 T(n/4)T(n/4)T(n/4)T(n/4) n/2 T(n/4)T(n/4)T(n/4)T(n/4) n/2 T(n/4)T(n/4)T(n/4)T(n/4) n/2 T(n/4)T(n/4)T(n/4)T(n/4)
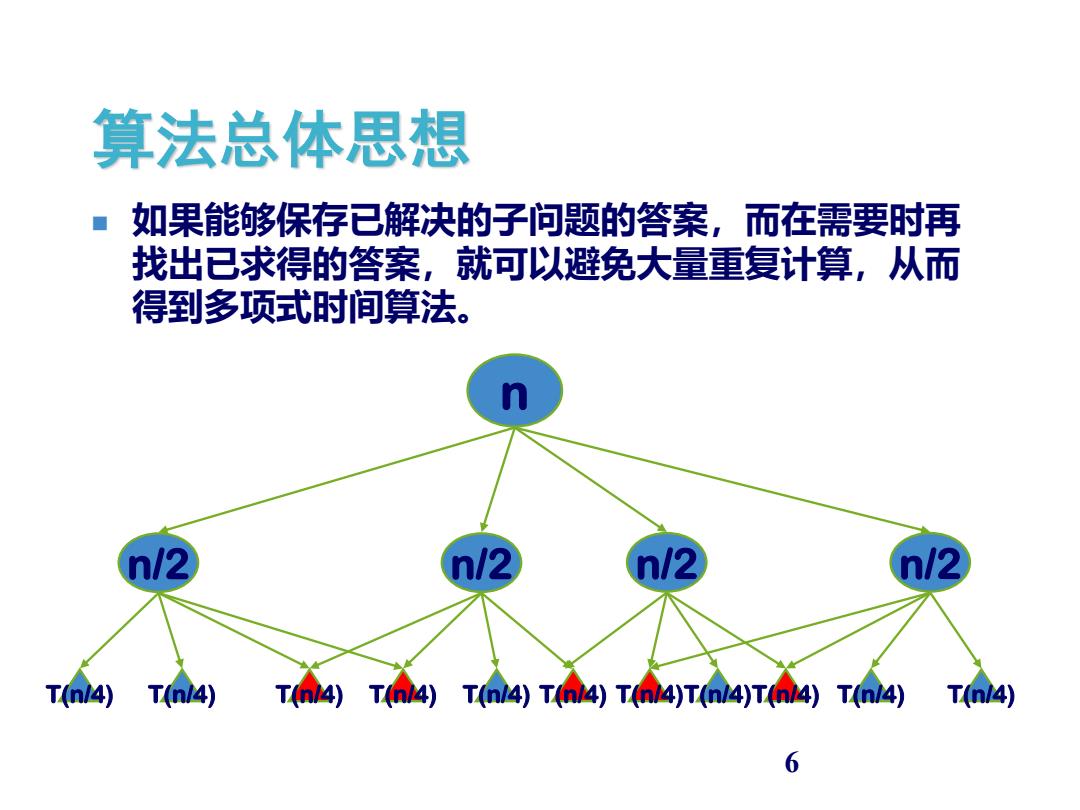
算法总体思想 ■ 如果能够保存已解决的子问题的答案,而在需要时再 找出已求得的答案,就可以避免大量重复计算,从而 得到多项式时间算法。 n12 n/2 n/2 n/2 T4)TA4)T64T(64)TA4)T(64)T(4)TA4T(4)T4) T64) 6
6 ◼ 如果能够保存已解决的子问题的答案,而在需要时再 找出已求得的答案,就可以避免大量重复计算,从而 得到多项式时间算法。 算法总体思想 n n/2 T(n/4) T(n/4) T(n/4) T(n/4) n/2 n/2 T(n/4)T(n/4) n/2 T(n/4) T(n/4) T(n/4) T(n/4) T(n/4)

动态规划算法 CR 算法总体思想 动态规划算法与分治法类似,其基本思想也是将待求解问题 分解成若干个子问题 ⊕ 与分治法的区别在于 适用于动态规划算法求解的问题,经分解得到的子问题往 往不是互相独立的;若用分治法求解,则分解得到的子问 题数目太多,导致最终解决原问题需指数时间, 原因在于:虽然子问题的数目常常只有多项式量级,但在 用分治法求解时,有些子问题被重复计算了许多次 ⊕ 如果可以保存已解决的子问题的答案,就可以避免大量重复 计算,从而得到多项式时间的算法 动态规划法的基本思路是:构造一张表来记录所有已解决的 子问题的答案(无论算法形式如何,其填表格式是相同的)
动态规划算法 算法总体思想 动态规划算法与分治法类似,其基本思想也是将待求解问题 分解成若干个子问题 与分治法的区别在于 ━ 适用于动态规划算法求解的问题,经分解得到的子问题往 往不是互相独立的;若用分治法求解,则分解得到的子问 题数目太多,导致最终解决原问题需指数时间, ━ 原因在于:虽然子问题的数目常常只有多项式量级,但在 用分治法求解时,有些子问题被重复计算了许多次 如果可以保存已解决的子问题的答案,就可以避免大量重复 计算,从而得到多项式时间的算法 动态规划法的基本思路是:构造一张表来记录所有已解决的 子问题的答案(无论算法形式如何,其填表格式是相同的)

动态规划算法的基本步骤 1。找出最优解的性质(分析其结构特征) 2.递归地定义最优值(优化目标函数) 3.以自底向上的方式计算出最优值 4.根据计算最优值时得到的信息,构造最优解
动态规划算法的基本步骤 1. 找出最优解的性质(分析其结构特征) 2. 递归地定义最优值(优化目标函数) 3. 以自底向上的方式计算出最优值 4. 根据计算最优值时得到的信息,构造最优解

3.1矩阵连乘问题 (Matrix-Chain Multiplication)
3.1 矩阵连乘问题 (Matrix-Chain Multiplication)

两个矩阵相乘:标准解法 void matrixMultiply(int **Ma,int **Mb,int **Mc, int ra,int ca,int rb,int cb){ if(caI=rb)error("矩阵不可乘"): for (int i=0;i<ra;i++) for (int j=0;j<cb;j++){ int sum=a[i][o]*b[o][j]; for (int k=1;k<ca;k++) sum +a[i][k]*b[k][j]; } c[i][j]=sum; } } 设A是pXq的矩阵,B是qXr的矩阵,数乘次数为pxqxr 算法的时间复杂度为:O(n3)
两个矩阵相乘:标准解法 • 设A是pⅹq的矩阵,B是qⅹr的矩阵,数乘次数为pⅹqⅹr • 算法的时间复杂度为:O(n3) void matrixMultiply( int **Ma, int **Mb, int **Mc, int ra, int ca, int rb, int cb ) { if (ca != rb) error(“矩阵不可乘”); for (int i=0; i<ra; i++){ for (int j=0; j<cb; j++) { int sum=a[i][0]*b[0][j]; for (int k=1; k<ca; k++){ sum += a[i][k]*b[k][j]; } c[i][j]=sum; } } }