
Design and Analysis of Algorithms 4.NP and Computational Intractability Mingyu XIAO School of Computer Science and Engineering University of Electronic Science and Technology of China
Design and Analysis of Algorithms 4. NP and Computational Intractability Mingyu XIAO School of Computer Science and Engineering University of Electronic Science and Technology of China

Algorithm Design Patterns and Anti-Patterns Algorithm design patterns. Ex. Greedy. O(n log n)interval scheduling. Divide-and-conquer. O(n log n)FFT. Dynamic programming. O(n2)edit distance. Duality. O(n3)bipartite matching. Reductions. Algorithm design anti-patterns. NP-completeness. O(nc)algorithm unlikely. PSPACE-completeness. O(nc)certification algorithm unlikely. Undecidability. No algorithm possible. 3
2 Algorithm Design Patterns and Anti-Patterns Algorithm design patterns. Ex. Greedy. O(n log n) interval scheduling. Divide-and-conquer. O(n log n) FFT. Dynamic programming. O(n2) edit distance. Duality. O(n3) bipartite matching. Reductions. Algorithm design anti-patterns. NP-completeness. O(nc ) algorithm unlikely. PSPACE-completeness. O(nc ) certification algorithm unlikely. Undecidability. No algorithm possible

4.1 Polynomial-Time Reductions
4.1 Polynomial-Time Reductions

Classify Problems According to Computational Requirements Q.Which problems will we be able to solve in practice? A working definition.[von Neumann 1953,Godel 1956,Cobham 1964,Edmonds 1965,Rabin 1966] Those with polynomial-time algorithms. Yes Probably no Shortest path Longest path Matching 3D-matching Min cut Max cut 2-SAT 3-SAT Planar 4-color Planar 3-color Bipartite vertex cover Vertex cover
4 Classify Problems According to Computational Requirements Q. Which problems will we be able to solve in practice? A working definition. [von Neumann 1953, Godel 1956, Cobham 1964, Edmonds 1965, Rabin 1966] Those with polynomial-time algorithms. Yes Probably no Shortest path Longest path Min cut Max cut 2-SAT 3-SAT Matching 3D-matching Planar 4-color Planar 3-color Bipartite vertex cover Vertex cover

Classify Problems Classes.Classify problems according to those that can be solved in polynomial-time and those that cannot. Frustrating news.Huge number of fundamental problems have defined classification for decades. This chapter.Show that these fundamental problems are "computationally equivalent"and appear to be different manifestations of one really hard problem. 5
5 Classify Problems Classes. Classify problems according to those that can be solved in polynomial-time and those that cannot. Frustrating news. Huge number of fundamental problems have defined classification for decades. This chapter. Show that these fundamental problems are "computationally equivalent" and appear to be different manifestations of one really hard problem

Polynomial-Time Reduction don't confuse with reduces from Reduction.Problem X polynomial reduces to problem y if arbitrary instances of problem X can be solved using: Polynomial number of standard computational steps,plus Polynomial number of calls to oracle that solves problem y. Notation.X≤py. computational model supplemented by special piece of hardware that solves instances of y in a single step Questions. Any requirement on the input size of y? 6
6 Polynomial-Time Reduction Reduction. Problem X polynomial reduces to problem Y if arbitrary instances of problem X can be solved using: Polynomial number of standard computational steps, plus Polynomial number of calls to oracle that solves problem Y. Notation. X P Y. don't confuse with reduces from computational model supplemented by special piece of hardware that solves instances of Y in a single step Questions. Any requirement on the input size of Y?

Polynomial-Time Reduction Purpose.Classify problems according to relative difficulty. Design algorithms.If X sp y and y can be solved in polynomial-time, then X can also be solved in polynomial time. Establish intractability.If Xsp y and X cannot be solved in polynomial-time,then y cannot be solved in polynomial time. Establish equivalence..IfX≤y and y≤pX,we use notation X≡py. \ up to cost of reduction 7
7 Polynomial-Time Reduction Purpose. Classify problems according to relative difficulty. Design algorithms. If X P Y and Y can be solved in polynomial-time, then X can also be solved in polynomial time. Establish intractability. If X P Y and X cannot be solved in polynomial-time, then Y cannot be solved in polynomial time. Establish equivalence. If X P Y and Y P X, we use notation X P Y. up to cost of reduction

Reduction By Simple Equivalence Basic reduction strategies. Reduction by simple equivalence. Reduction from special case to general case. Reduction by encoding with gadgets
Reduction By Simple Equivalence Basic reduction strategies. Reduction by simple equivalence. Reduction from special case to general case. Reduction by encoding with gadgets
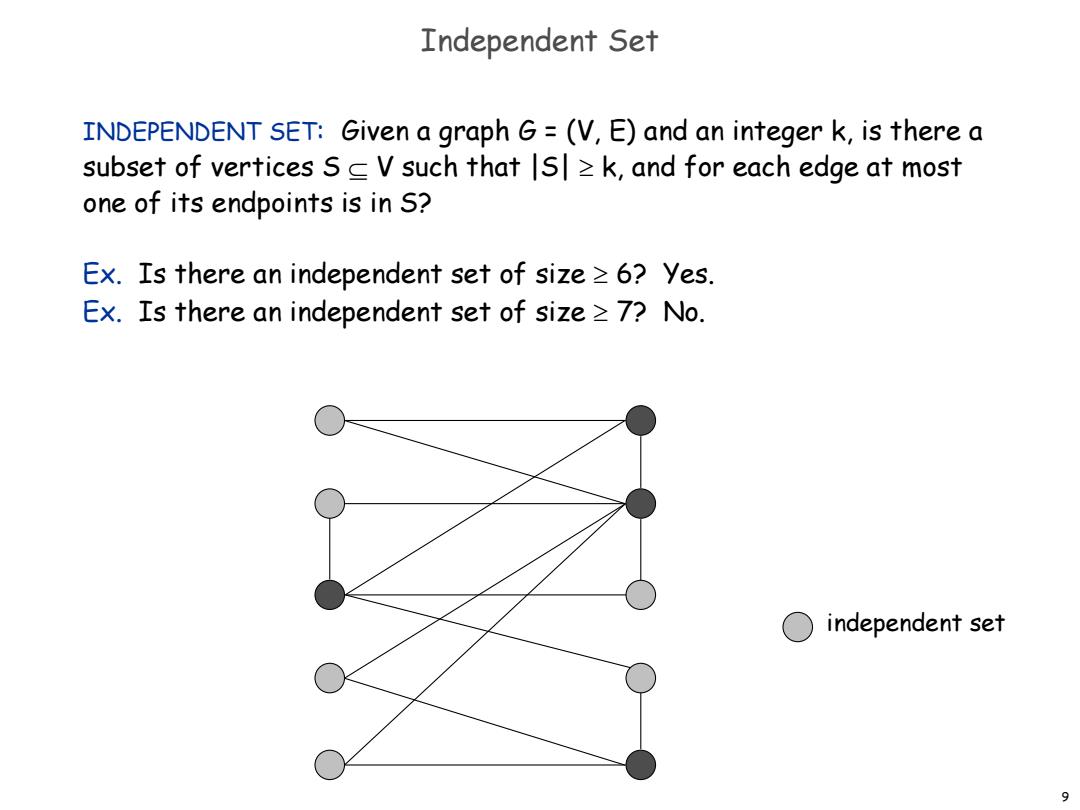
Independent Set INDEPENDENT SET:Given a graph G=(V,E)and an integer k,is there a subset of vertices sc V such that s>k,and for each edge at most one of its endpoints is in S? Ex.Is there an independent set of size≥6?yes. Ex.Is there an independent set of size≥7?No. ○independent set 9
9 Independent Set INDEPENDENT SET: Given a graph G = (V, E) and an integer k, is there a subset of vertices S V such that |S| k, and for each edge at most one of its endpoints is in S? Ex. Is there an independent set of size 6? Yes. Ex. Is there an independent set of size 7? No. independent set

Vertex Cover VERTEX COVER:Given a graph G=(V,E)and an integer k,is there a subset of vertices S V such that ISI s k,and for each edge,at least one of its endpoints is in S? Ex.Is there a vertex cover of size≤4?yes. Ex.Is there a vertex cover of size≤3?No. vertex cover 10
10 Vertex Cover VERTEX COVER: Given a graph G = (V, E) and an integer k, is there a subset of vertices S V such that |S| k, and for each edge, at least one of its endpoints is in S? Ex. Is there a vertex cover of size 4? Yes. Ex. Is there a vertex cover of size 3? No. vertex cover