
Design and Analysis of Algorithms 3.Maximum Flow Mingyu XIAO School of Computer Science and Engineering University of Electronic Science and Technology of China
Design and Analysis of Algorithms 3. Maximum Flow Mingyu XIAO School of Computer Science and Engineering University of Electronic Science and Technology of China
Soviet Rail Network,1955 G5 幽 蹈韶奥 ®6 2 蝇 5 8 o大 ⑧ 2 3 ORIGINS Reference:On the history of the transportation and maximum flow problems. Alexander Schrijver in Math Programming,91:3,2002. 2
2 Soviet Rail Network, 1955 Reference: On the history of the transportation and maximum flow problems. Alexander Schrijver in Math Programming, 91: 3, 2002

Maximum Flow and Minimum Cut Max flow and min cut. Two very rich algorithmic problems. Cornerstone problems in combinatorial optimization. Beautiful mathematical duality. Nontrivial applications reductions. Data mining. Network reliability. Open-pit mining. Distributed computing. Project selection. Egalitarian stable matching. Airline scheduling. Security of statistical data. Bipartite matching. Network intrusion detection. Baseball elimination. Multi-camera scene ·Image segmentation. reconstruction. Network connectivity. Many many more .. 3
3 Maximum Flow and Minimum Cut Max flow and min cut. Two very rich algorithmic problems. Cornerstone problems in combinatorial optimization. Beautiful mathematical duality. Nontrivial applications / reductions. Data mining. Open-pit mining. Project selection. Airline scheduling. Bipartite matching. Baseball elimination. Image segmentation. Network connectivity. Network reliability. Distributed computing. Egalitarian stable matching. Security of statistical data. Network intrusion detection. Multi-camera scene reconstruction. Many many more …

Minimum Cut Problem Flow network. Abstraction for material flowing through the edges. G =(V,E)=directed graph,no parallel edges. Two distinguished nodes:s source,t=sink. c(e)capacity of edge e. 9 5 10 15 15 4 10 source(s 8 10 sink 6 15 15 10 capacity 30 4
4 Flow network. Abstraction for material flowing through the edges. G = (V, E) = directed graph, no parallel edges. Two distinguished nodes: s = source, t = sink. c(e) = capacity of edge e. Minimum Cut Problem s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 capacity source sink
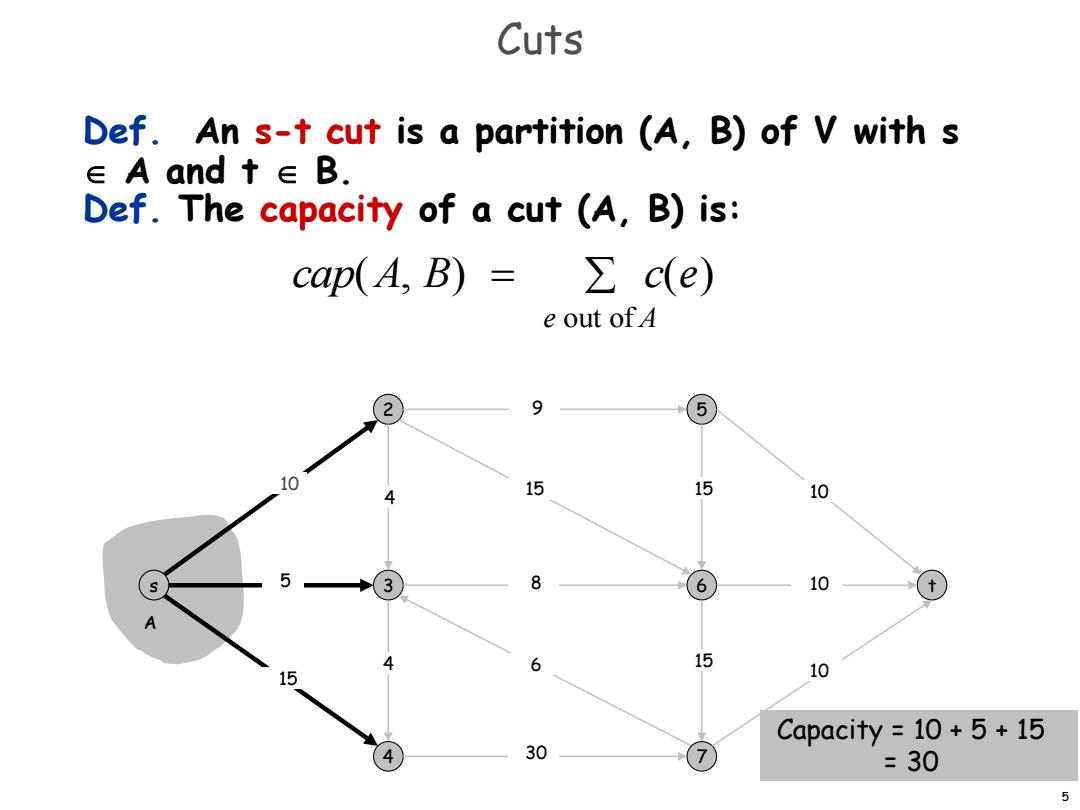
Cuts Def.An s-t cut is a partition (A,B)of V with s ∈A and t∈B. Def.The capacity of a cut (A,B)is: cap(A,B)= ∑c(e) e out of 4 2 9 10 4 15 15 10 5 3 8 6 10 6 15 15 10 Capacity =10+5+15 4 30 7 =30 5
5 Def. An s-t cut is a partition (A, B) of V with s A and t B. Def. The capacity of a cut (A, B) is: Cuts s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 Capacity = 10 + 5 + 15 = 30 A cap(A, B) c(e) e out of A
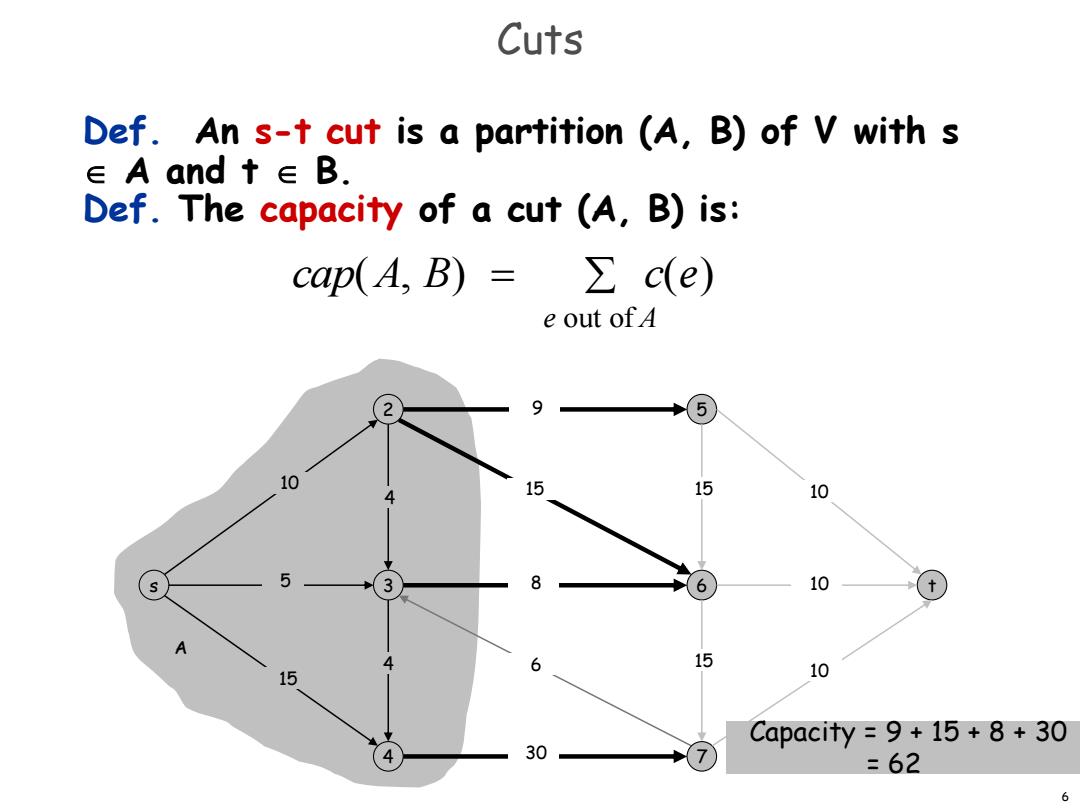
Cuts Def.An s-t cut is a partition (A,B)of V with s ∈A and t∈B. Def.The capacity of a cut (A,B)is: cap(A,B)=∑c(e) e out of 4 2 9 5 10 15 15 10 s 5 8 6 10 A 6 15 15 10 Capacity =9+15+8+30 30 7 =62 6
6 Def. An s-t cut is a partition (A, B) of V with s A and t B. Def. The capacity of a cut (A, B) is: Cuts cap(A, B) c(e) e out of A s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 A Capacity = 9 + 15 + 8 + 30 = 62
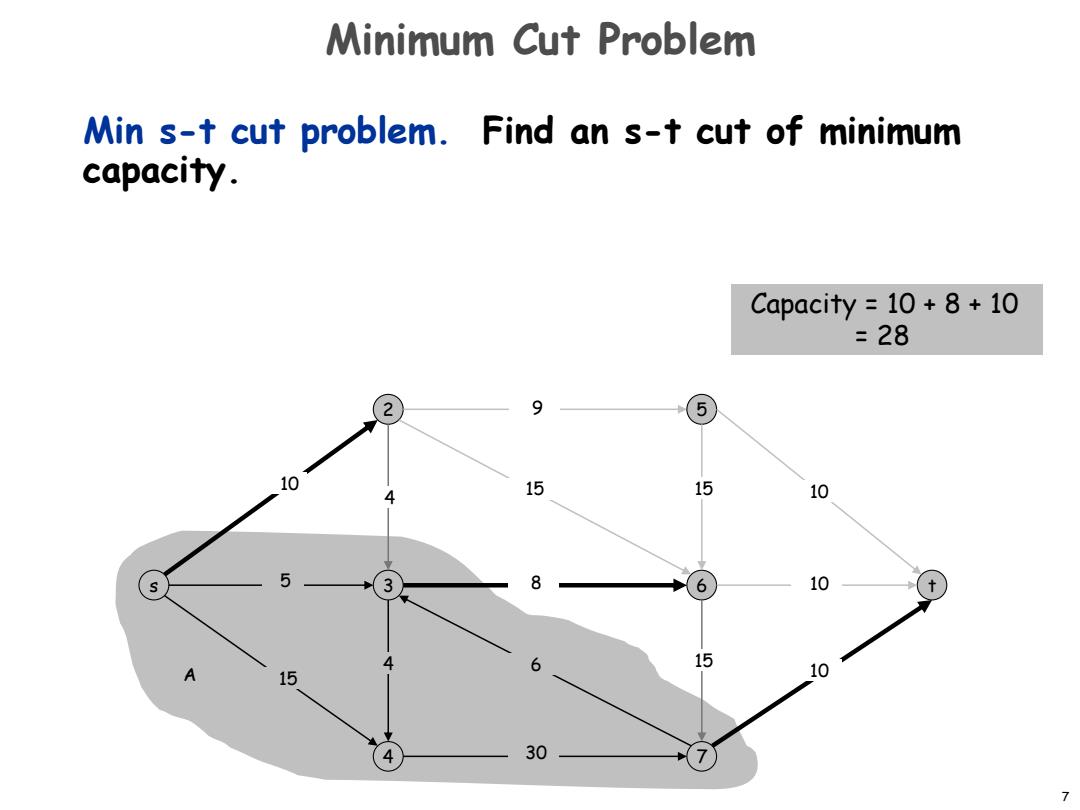
Minimum Cut Problem Min s-t cut problem.Find an s-t cut of minimum capacity. Capacity 10+8+10 =28 9 5 10 15 4 15 10 5 3 8 6 10 4 6 15 A 15 10 4 30 7
7 Min s-t cut problem. Find an s-t cut of minimum capacity. Minimum Cut Problem s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 A Capacity = 10 + 8 + 10 = 28
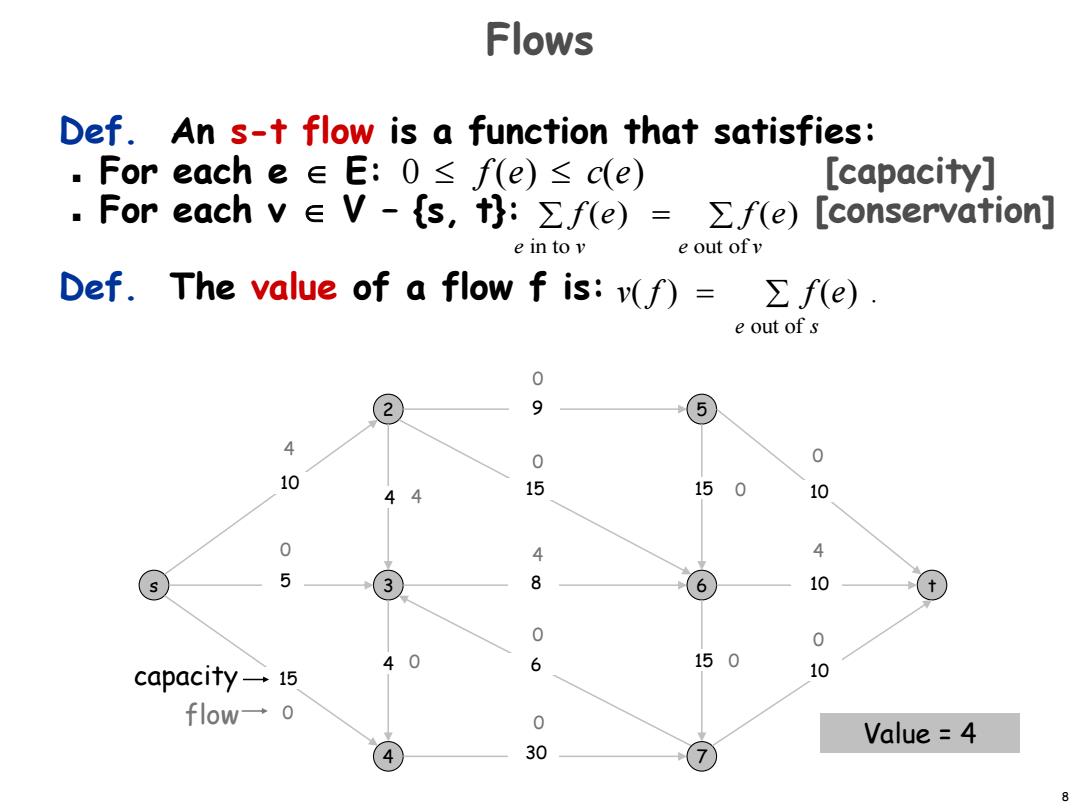
Flows Def.An s-t flow is a function that satisfies: .For each e∈E:0≤f(e)≤c(e) [capacity] .For each v∈V-s,t:Σf(e)=∑f(e)[conservation] e in to v e out ofv Def.The value of a flow f is:v(f)= ∑f(e). e out ofs 0 2 9 5 4 0 0 10 44 15 150 10 0 4 4 5 3 8 6 10 0 40 6 150 capacity一15 10 flow一0 0 Value =4 4 30 8
8 Def. An s-t flow is a function that satisfies: For each e E: [capacity] For each v V – {s, t}: [conservation] Def. The value of a flow f is: Flows 4 0 0 0 0 0 0 4 4 0 0 0 Value = 4 0 f (e) e in to v f (e) e out of v 0 f (e) c(e) capacity flow s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 0 v( f ) f (e) e out of s . 4
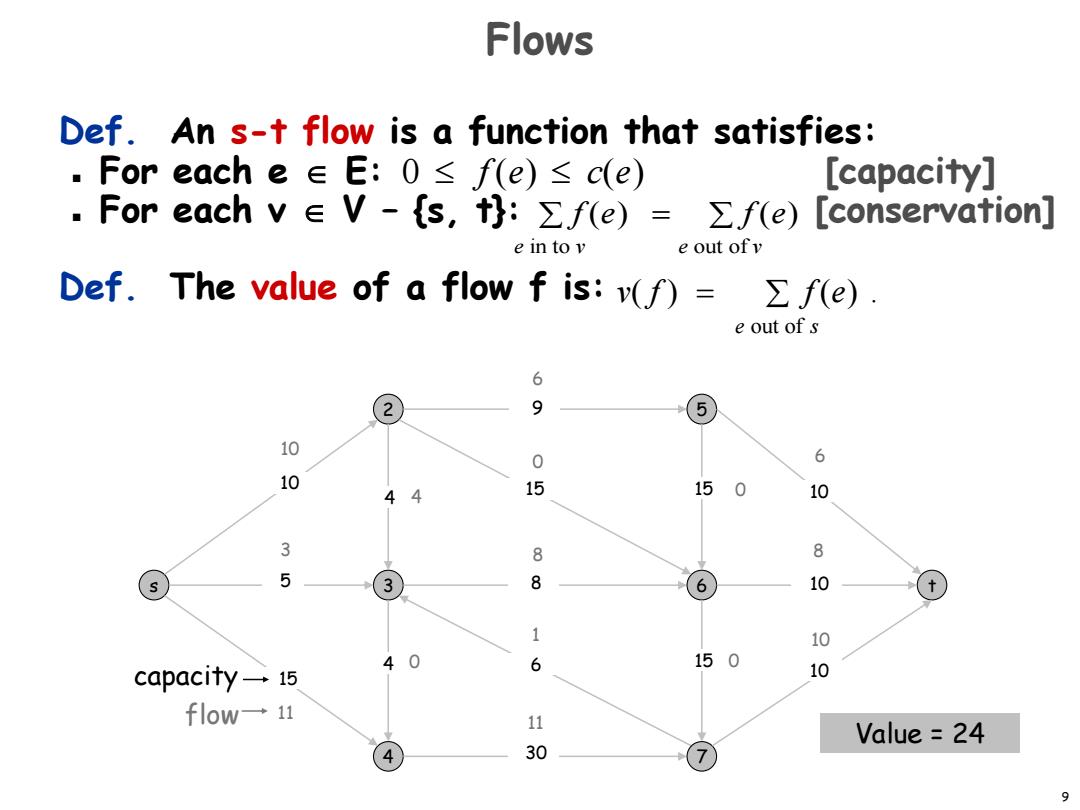
Flows Def.An s-t flow is a function that satisfies: .For each e∈E:0≤f(e)≤c(e) [capacity] .For each v∈V-s,t:Σf(e)=∑f(e)[conservation] e in to v e out ofv Def.The value of a flow f is:v(f)= ∑f(e). e out ofs 6 2 9 5 10 0 6 10 44 15 150 10 3 8 8 5 3 8 6 10 1 10 40 6 150 capacity一15 10 flow→11 11 Value 24 4 30 9
9 Def. An s-t flow is a function that satisfies: For each e E: [capacity] For each v V – {s, t}: [conservation] Def. The value of a flow f is: Flows Value = 24 f (e) e in to v f (e) e out of v 0 f (e) c(e) capacity flow v( f ) f (e) e out of s . 10 6 6 11 1 10 3 8 8 0 0 0 11 s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 0 4
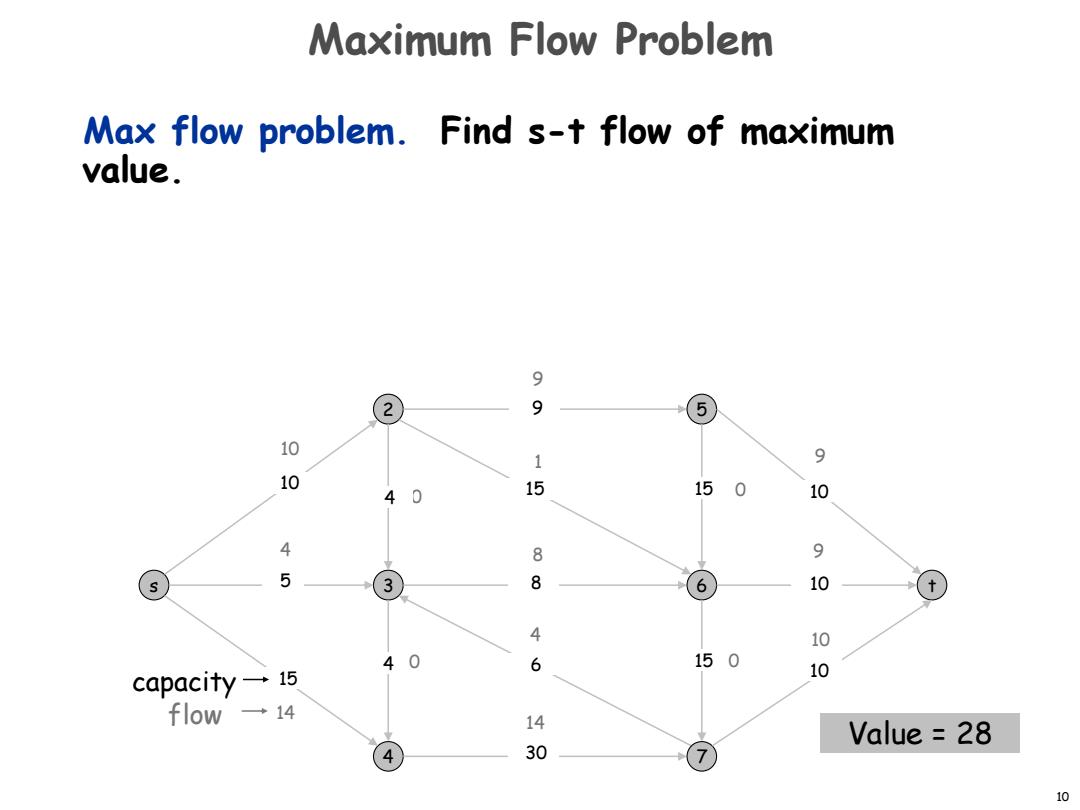
Maximum Flow Problem Max flow problem.Find s-t flow of maximum value. 9 2 9 5 10 1 9 10 40 15 150 10 4 8 9 5 3 8 6 10 4 10 40 6 150 capacity一15 10 flow一14 14 Value 28 4 30 7 10
10 Max flow problem. Find s-t flow of maximum value. Maximum Flow Problem 10 9 9 14 4 10 4 8 9 1 0 0 0 14 capacity flow s 2 3 4 5 6 7 t 15 5 30 15 10 8 15 9 6 10 10 15 10 4 4 0 Value = 28