
Design and Analysis of Algorithms 5.Approximation Algorithms Mingyu XIAO School of Computer Science and Engineering University of Electronic Science and Technology of China
Design and Analysis of Algorithms 5. Approximation Algorithms Mingyu XIAO School of Computer Science and Engineering University of Electronic Science and Technology of China

Approximation Algorithms Q.Suppose I need to solve an NP-hard problem.What should I do? A.Theory says you're unlikely to find a poly-time algorithm. Must sacrifice one of three desired features. Solve problem to optimality. Solve problem in poly-time. Solve arbitrary instances of the problem. p-approximation algorithm. Guaranteed to run in poly-time. Guaranteed to solve arbitrary instance of the problem Guaranteed to find solution within ratio p of true optimum. Challenge.Need to prove a solution's value is close to optimum,without even knowing what optimum value is! 2
2 Approximation Algorithms Q. Suppose I need to solve an NP-hard problem. What should I do? A. Theory says you're unlikely to find a poly-time algorithm. Must sacrifice one of three desired features. Solve problem to optimality. Solve problem in poly-time. Solve arbitrary instances of the problem. -approximation algorithm. Guaranteed to run in poly-time. Guaranteed to solve arbitrary instance of the problem Guaranteed to find solution within ratio of true optimum. Challenge. Need to prove a solution's value is close to optimum, without even knowing what optimum value is!
5.1 Load Balancing
5.1 Load Balancing

Load Balancing Input.m identical machines;n jobs,job j has processing time tj. Job j must run contiguously on one machine. A machine can process at most one job at a time. Def.Let J(i)be the subset of jobs assigned to machine i.The load of machine i is Li=>jeJ(i)fj. Def.The makespan is the maximum load on any machine L max;Li. Load balancing.Assign each job to a machine to minimize makespan
4 Load Balancing Input. m identical machines; n jobs, job j has processing time tj . Job j must run contiguously on one machine. A machine can process at most one job at a time. Def. Let J(i) be the subset of jobs assigned to machine i. The load of machine i is Li = j J(i) tj . Def. The makespan is the maximum load on any machine L = maxi Li . Load balancing. Assign each job to a machine to minimize makespan

Load Balancing:List Scheduling List-scheduling algorithm. Consider n jobs in some fixed order. D Assign job j to machine whose load is smallest so far. List-Scheduling(m,n,t1,t2,...,tn){ for i=1 to m 工1←0 load on machine i J(i)←中- jobs assigned to machine i } for j=1 to n i=argmink Lk machine i has smallest load J(i)←J(i)U{} assign job j to machine i 工:←工:+t与 update load of machine i return J(1),…,J(m) Implementation.O(n log m)using a priority queue. 5
5 List-scheduling algorithm. Consider n jobs in some fixed order. Assign job j to machine whose load is smallest so far. Implementation. O(n log m) using a priority queue. Load Balancing: List Scheduling List-Scheduling(m, n, t1,t2,…,tn) { for i = 1 to m { Li 0 J(i) } for j = 1 to n { i = argmink Lk J(i) J(i) {j} Li Li + tj } return J(1), …, J(m) } jobs assigned to machine i load on machine i machine i has smallest load assign job j to machine i update load of machine i

Load Balancing:List Scheduling Analysis Theorem.[Graham,1966]Greedy algorithm is a 2-approximation. First worst-case analysis of an approximation algorithm. Need to compare resulting solution with optimal makespan L*. Lemma 1.The optimal makespan L*maxj tj. Pf.Some machine must process the most time-consuming job. Lemma2.The optimal makespan L*≥a∑,t,: Pf. The total processing time is >jtj. One of m machines must do at least a 1/m fraction of total work. 6
6 Load Balancing: List Scheduling Analysis Theorem. [Graham, 1966] Greedy algorithm is a 2-approximation. First worst-case analysis of an approximation algorithm. Need to compare resulting solution with optimal makespan L*. Lemma 1. The optimal makespan L* maxj tj . Pf. Some machine must process the most time-consuming job. ▪ Lemma 2. The optimal makespan Pf. The total processing time is j tj . One of m machines must do at least a 1/m fraction of total work. ▪ L * 1 m t j j
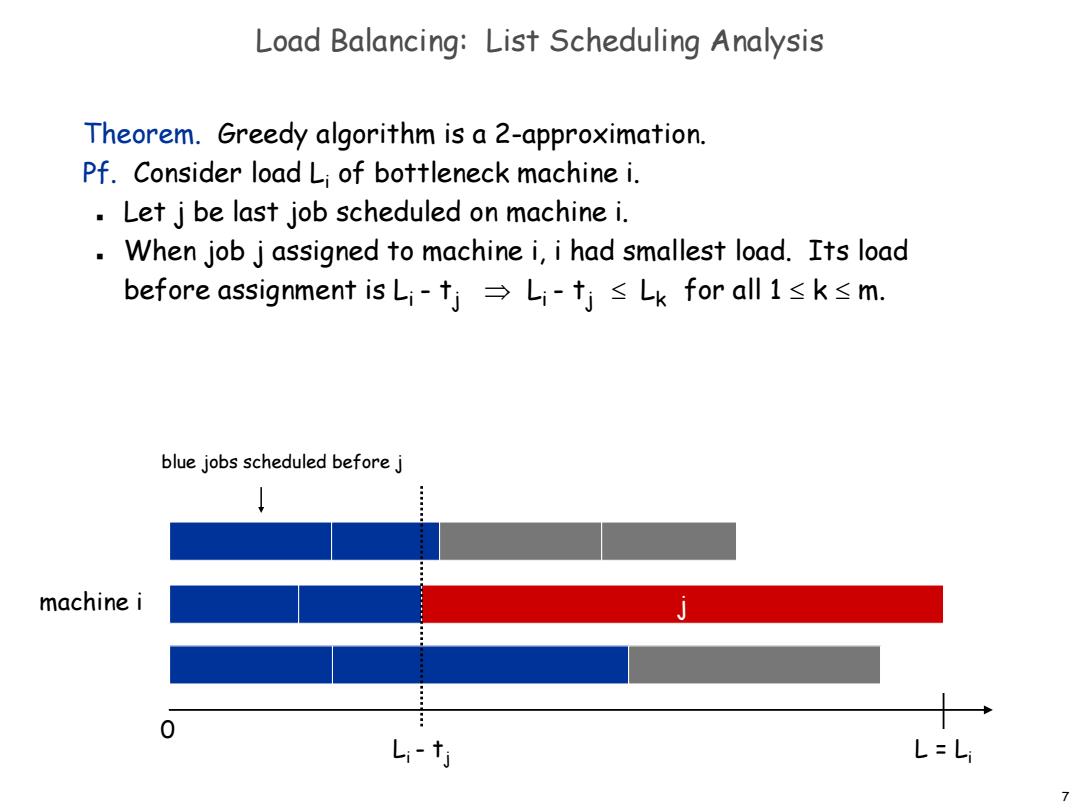
Load Balancing:List Scheduling Analysis Theorem.Greedy algorithm is a 2-approximation. Pf.Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i,i had smallest load.Its load before assignment is Li-tj→Li-tj≤Lk for all1≤k≤m. blue jobs scheduled before j machine i Li-tj L=L: 7
7 Load Balancing: List Scheduling Analysis Theorem. Greedy algorithm is a 2-approximation. Pf. Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i, i had smallest load. Its load before assignment is Li - tj Li - tj Lk for all 1 k m. j 0 Li L = Li - tj machine i blue jobs scheduled before j

Load Balancing:List Scheduling Analysis Theorem.Greedy algorithm is a 2-approximation. Pf.Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i,i had smallest load.Its load before assignment is Li-tj→Li-tj≤Lk for all1≤k≤m. Sum inegualities over all k and divide by m: L,-4≤a∑kL h∑k Lemma 1 ≤L* ·NowL;=(L,-4)+t) ≤2L*. ≤L* ≤L米 1 Lemma 2 8
8 Load Balancing: List Scheduling Analysis Theorem. Greedy algorithm is a 2-approximation. Pf. Consider load Li of bottleneck machine i. Let j be last job scheduled on machine i. When job j assigned to machine i, i had smallest load. Its load before assignment is Li - tj Li - tj Lk for all 1 k m. Sum inequalities over all k and divide by m: Now ▪ Li t j 1 m k Lk 1 m t k k L * Li (Li t j ) L* t j L* 2L *. Lemma 2 Lemma 1
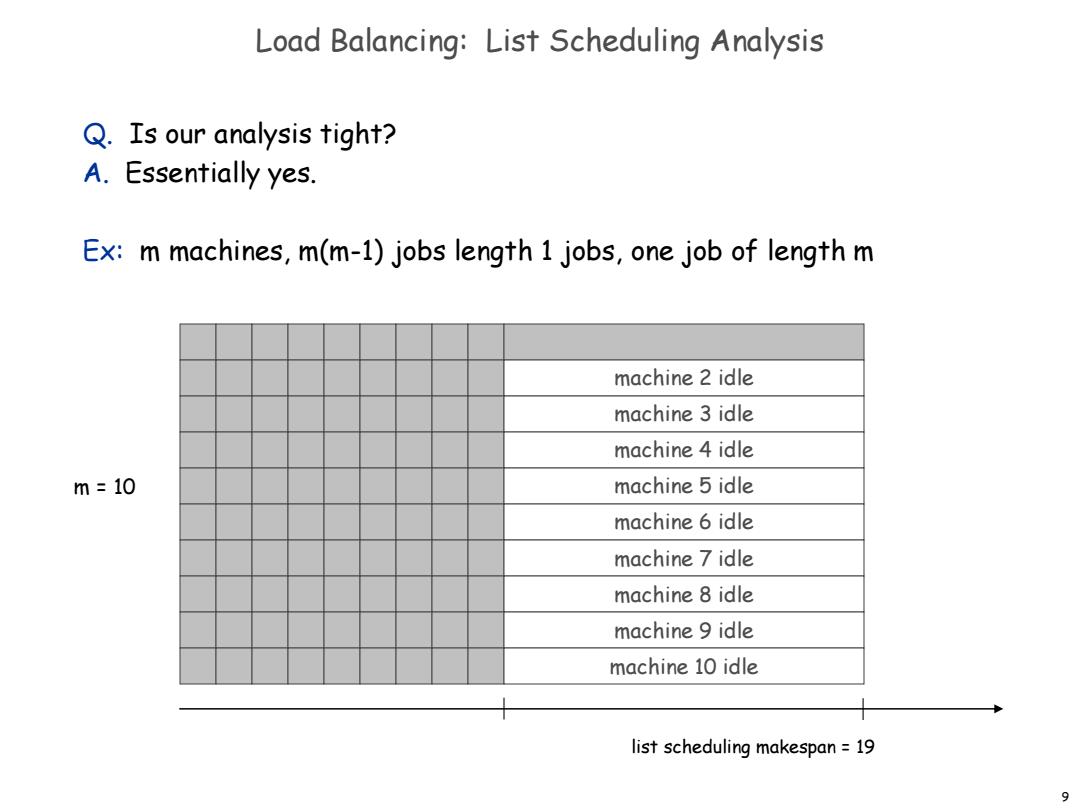
Load Balancing:List Scheduling Analysis Q.Is our analysis tight? A.Essentially yes. Ex:m machines,m(m-1)jobs length 1 jobs,one job of length m machine 2 idle machine 3 idle machine 4 idle m=10 machine 5 idle machine 6 idle machine 7 idle machine 8 idle machine 9 idle machine 10 idle list scheduling makespan 19 9
9 Load Balancing: List Scheduling Analysis Q. Is our analysis tight? A. Essentially yes. Ex: m machines, m(m-1) jobs length 1 jobs, one job of length m machine 2 idle machine 3 idle machine 4 idle machine 5 idle machine 6 idle machine 7 idle machine 8 idle machine 9 idle machine 10 idle list scheduling makespan = 19 m = 10
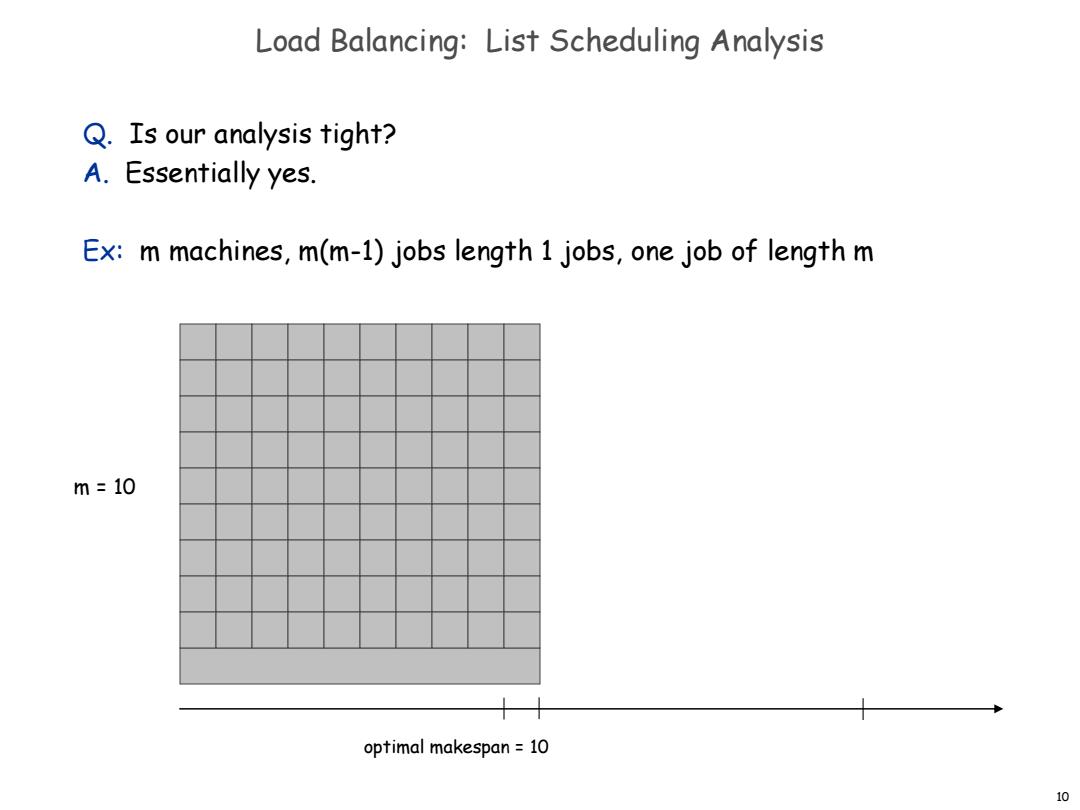
Load Balancing:List Scheduling Analysis Q.Is our analysis tight? A.Essentially yes. Ex:m machines,m(m-1)jobs length 1 jobs,one job of length m m=10 optimal makespan 10 10
10 Load Balancing: List Scheduling Analysis Q. Is our analysis tight? A. Essentially yes. Ex: m machines, m(m-1) jobs length 1 jobs, one job of length m m = 10 optimal makespan = 10