
第2章:递归与分治策略
第2章:递归与分治策略

知识要点 3递割归的概念和典型的递归问题 Φ阶乘、Fibonacci数列、hanoif塔等问题 ?分治法的基本思想 3分治法的典型例子 Φ二分搜索、矩阵乘法、归并排序、快速排序 Φ大整数的乘法、最接近点对问题
知识要点 递归的概念和典型的递归问题 阶乘、Fibonacci数列、hanoi塔等问题 分治法的基本思想 分治法的典型例子 二分搜索、矩阵乘法、归并排序、快速排序 大整数的乘法、最接近点对问题

2.1递归的概念
2.1 递归的概念

递归(recursion) R 什么是递归? 程序调用自身的编程技巧称为递归 Φ 基本思路 。将一个大型的复杂问题转化为 一些与原问题相似的规模较小的问题来求解
递归(recursion) 什么是递归? 程序调用自身的编程技巧称为递归 基本思路 • 将一个大型的复杂问题转化为 • 一些与原问题相似的规模较小的问题来求解

递归(recursive) R 如果函数调用它本身,那么此函数就是递归的 3 例如n的定义就是递归的:n!=n×(n-1)川 R 考察下面的函数: int fact(int n) { 递归终止条件 if(n<=1)7/初值,1!=1 return 1; else 递归 return n fact(n -1); 表达式 } R 为了解递归的工作原理,我们来跟踪fact(4)的执行
递归(recursive) 如果函数调用它本身,那么此函数就是递归的 例如n!的定义就是递归的:n! = n × (n – 1)! 考察下面的函数: int fact(int n) { if (n <= 1) //初值,1!=1 return 1; else return n * fact(n - 1); } 为了解递归的工作原理,我们来跟踪 fact(4) 的执行 递归终止条件 递归 表达式

调用函数时系统的工作 3在调用函数时系统需要完成3件事: 将所有实参(指针),返回地址传递给被调用的函数 为被调用函数的局部变量分配存储区 将控制转移到被调用函数的入口 3从被调用函数返回时系统也要做3件事: 保存被调用算法的计算结果(返回值) 释放分配给被调用算法的存储空间 依照被调算法保存的返回地址将控制转移回到调用算法
调用函数时系统的工作 在调用函数时系统需要完成3件事: 将所有实参(指针),返回地址传递给被调用的函数 为被调用函数的局部变量分配存储区 将控制转移到被调用函数的入口 从被调用函数返回时系统也要做3件事: 保存被调用算法的计算结果(返回值) 释放分配给被调用算法的存储空间 依照被调算法保存的返回地址将控制转移回到调用算法

递归过程与递归工作栈 3递割归过程执行时需多次调用自身。多个(相同)函数 嵌套调用,信息传递和控制转移通过栈实现 Φ每一次递归调用时,需要为过程中所使用的参数、局部 变量等另外分配存储空间 层层向下递归,退出时次序正好相反 每层递归调用需分配的空间形成递归工作记录,用栈按 照后进先出规侧管理这些信息
递归过程与递归工作栈 递归过程执行时需多次调用自身。多个(相同)函数 嵌套调用,信息传递和控制转移通过栈实现 每一次递归调用时,需要为过程中所使用的参数、局部 变量等另外分配存储空间 层层向下递归,退出时次序正好相反 每层递归调用需分配的空间形成递归工作记录,用栈按 照后进先出规则管理这些信息
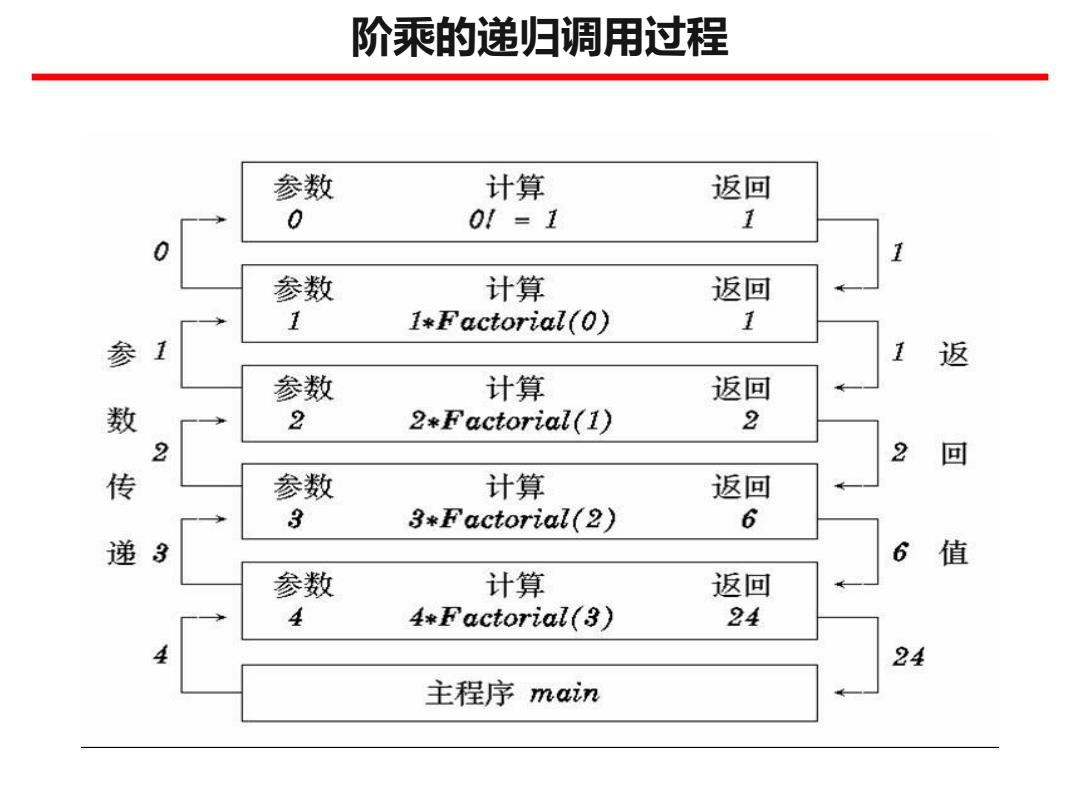
阶乘的递归调用过程 参数 计算 返回 0 01=1 1 0 参数 计算 返回 1 1*Factorial(0) 1 参 1 返 参数 计算 返回 数 2 2*Factorial(1) 2 2 2 回 传 参数 计算 返回 3 3*Factorial(2) 6 递 3 6 值 参数 计算 返回 4 4*Factorial(3) 24 4 24 主程序main
阶乘的递归调用过程
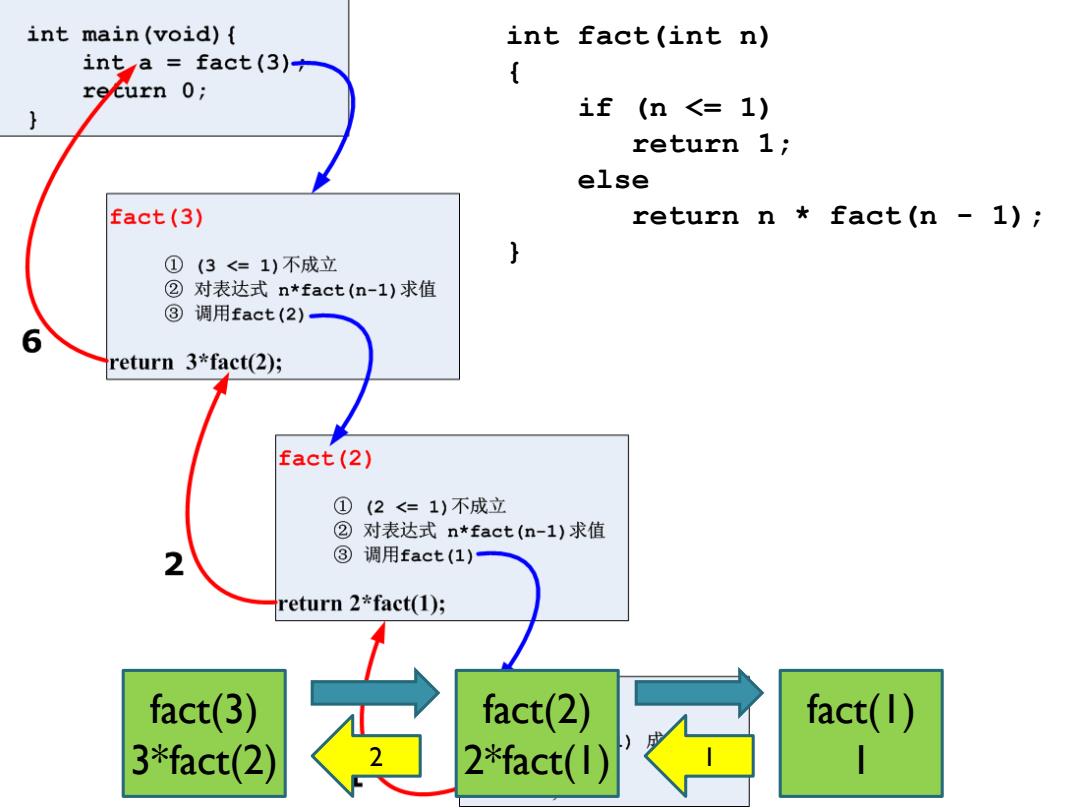
int main(void){ int fact(int n) int a fact(3) { recurn 0; if(n<=1) return 1; else fact(3) return n fact(n -1); ①(3<=1)不成立 ②对表达式n*fact(n-1)求值 ③调用fact(2) 6 return 3*fact(2); fact(2) ①(2<=1)不成立 ②对表达式n*fact(n-l)求值 2 ③调用fact(1)一 return 2*fact(1); fact(3) 3*fact(2) 3 fact(2) fact(1) 2*fact(1)
int fact(int n) { if (n <= 1) return 1; else return n * fact(n - 1); } fact(3) 3*fact(2) fact(2) 2*fact(1) fact(1) 2 1 1

递归的应用场景 3遇到如下三种情况,可以考虑使用递割归 1.问题定义是递归的 2.解决问题时采用的数据结构是递归定义的 3.问题的求解过程是递归的
递归的应用场景 遇到如下三种情况,可以考虑使用递归 1. 问题定义是递归的 2. 解决问题时采用的数据结构是递归定义的 3. 问题的求解过程是递归的