
Stable Matching
Stable Matching

Matching Residents to Hospitals Goal.Given a set of preferences among hospitals and medical school students,design a self-reinforcing admissions process. Unstable pair:applicant x and hospital y are unstable if: x prefers y to its assigned hospital. y prefers x to one of its admitted students. Stable assignment.Assignment with no unstable pairs. Natural and desirable condition. Individual self-interest will prevent any applicant/hospital deal from being made
3 Matching Residents to Hospitals Goal. Given a set of preferences among hospitals and medical school students, design a self-reinforcing admissions process. Unstable pair: applicant x and hospital y are unstable if: x prefers y to its assigned hospital. y prefers x to one of its admitted students. Stable assignment. Assignment with no unstable pairs. Natural and desirable condition. Individual self-interest will prevent any applicant/hospital deal from being made
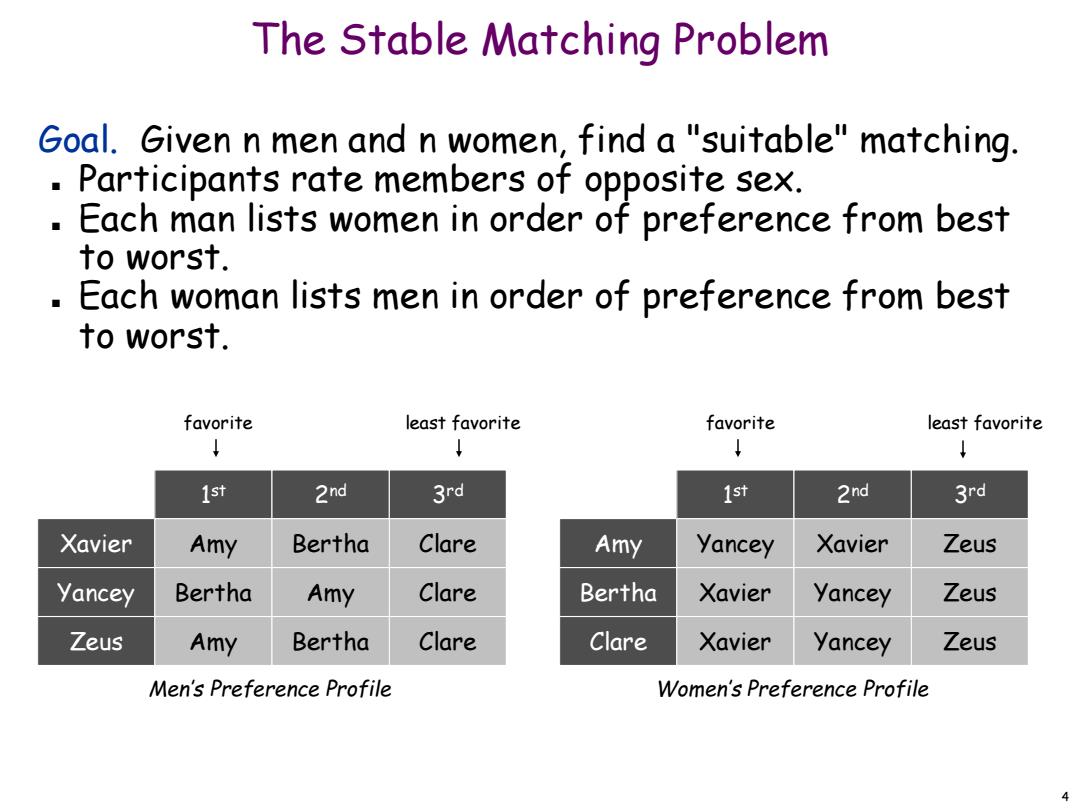
The Stable Matching Problem Goal.Given n men and n women,find a "suitable"matching. Participants rate members of opposite sex. Each man lists women in order of preference from best to worst. 。 Each woman lists men in order of preference from best to worst. favorite least favorite favorite least favorite 1st 2nd 3rd 1st 2nd 3rd Xavier Amy Bertha Clare Amy Yancey Xavier Zeus Yancey Bertha Amy Clare Bertha Xavier Yancey Zeus Zeus Amy Bertha Clare Clare Xavier Yancey Zeus Men's Preference Profile Women's Preference Profile 4
4 The Stable Matching Problem Goal. Given n men and n women, find a "suitable" matching. Participants rate members of opposite sex. Each man lists women in order of preference from best to worst. Each woman lists men in order of preference from best to worst. Zeus Amy Bertha Clare Yancey Bertha Amy Clare Xavier Amy Bertha Clare 1 st 2nd 3rd Men’s Preference Profile favorite least favorite Clare Xavier Yancey Zeus Bertha Xavier Yancey Zeus Amy Yancey Xavier Zeus 1 st 2nd 3rd Women’s Preference Profile favorite least favorite

The Stable Matching Problem Perfect matching:everyone is matched monogamously. Each man gets exactly one woman. Each woman gets exactly one man. Stability:no incentive for some pair of participants to undermine assignment by joint action. In matching M,an unmatched pair m-w is unstable if man m and woman w prefer each other to current partners. Unstable pair m-w could each improve by eloping. Stable matching:perfect matching with no unstable pairs. Stable matching problem.Given the preference lists of n men and n women,find a stable matching if one exists. 5
5 The Stable Matching Problem Perfect matching: everyone is matched monogamously. Each man gets exactly one woman. Each woman gets exactly one man. Stability: no incentive for some pair of participants to undermine assignment by joint action. In matching M, an unmatched pair m-w is unstable if man m and woman w prefer each other to current partners. Unstable pair m-w could each improve by eloping. Stable matching: perfect matching with no unstable pairs. Stable matching problem. Given the preference lists of n men and n women, find a stable matching if one exists
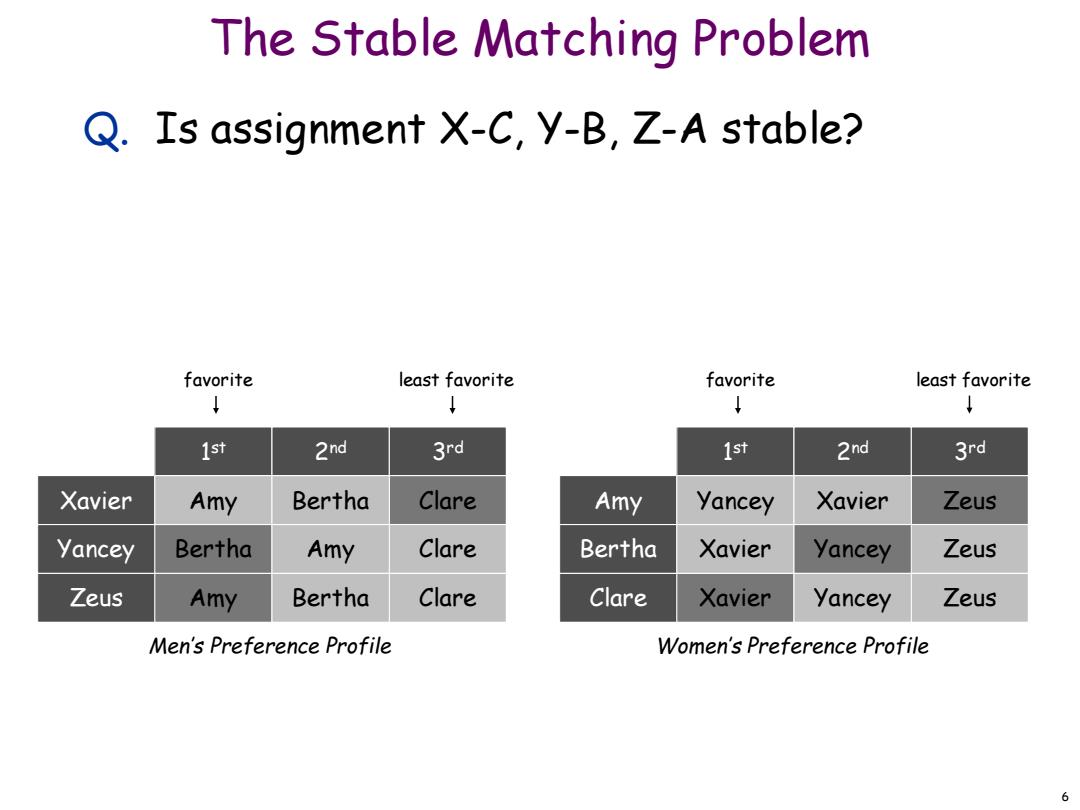
The Stable Matching Problem Q.Is assignment X-C,y-B,Z-A stable? favorite least favorite favorite least favorite 1st 2nd 3rd 1st 2nd 3rd Xavier Amy Bertha Clare Amy Yancey Xavier Zeus Yancey Bertha Amy Clare Bertha Xavier Yancey Zeus Zeus Amy Bertha Clare Clare Xavier Yancey Zeus Men's Preference Profile Women's Preference Profile 6
6 The Stable Matching Problem Q. Is assignment X-C, Y-B, Z-A stable? Zeus Amy Bertha Clare Yancey Bertha Amy Clare Xavier Amy Bertha Clare 1 st 2nd 3rd Men’s Preference Profile Clare Xavier Yancey Zeus Bertha Xavier Yancey Zeus Amy Yancey Xavier Zeus 1 st 2nd 3rd Women’s Preference Profile favorite least favorite favorite least favorite
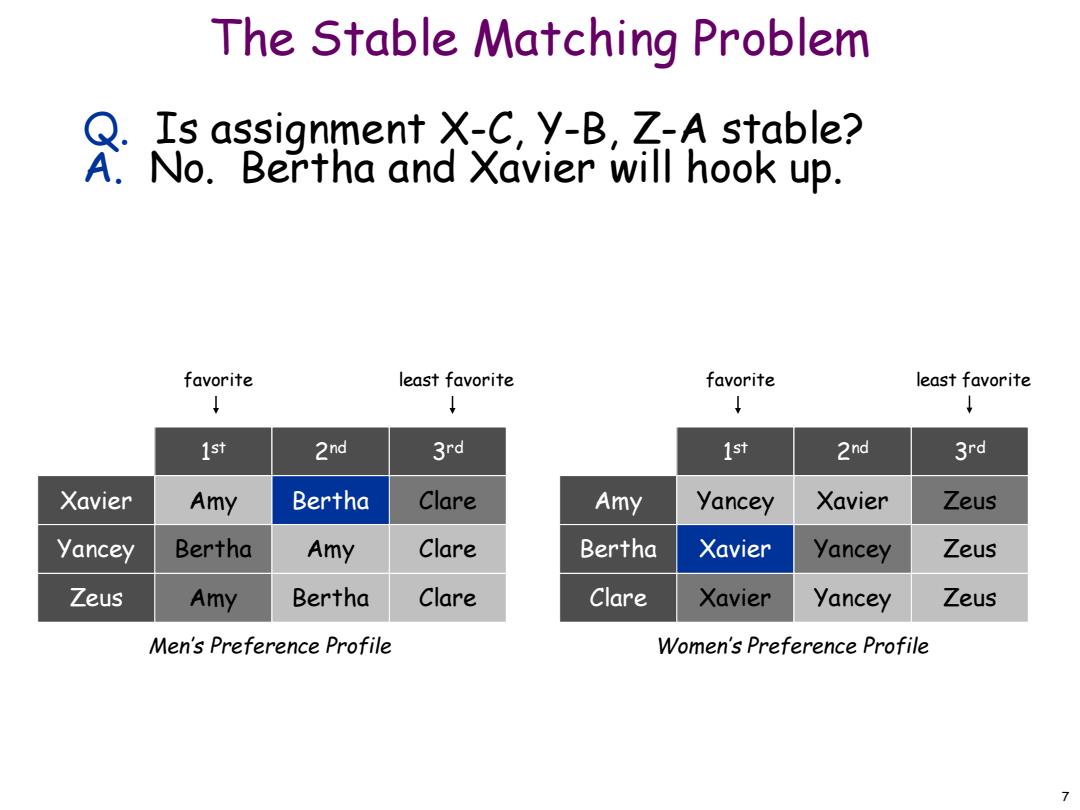
The Stable Matching Problem Is assignment X-C,y-B,Z-A stable? A.No.Bertha and Xavier will hook up. favorite least favorite favorite least favorite ↓ 1st 2nd 3rd 1st 2nd 3rd Xavier Amy Bertha Clare Amy Yancey Xavier Zeus Yancey Bertha Amy Clare Bertha Xavier Yancey Zeus Zeus Amy Bertha Clare Clare Xavier Yancey Zeus Men's Preference Profile Women's Preference Profile 7
7 The Stable Matching Problem Q. Is assignment X-C, Y-B, Z-A stable? A. No. Bertha and Xavier will hook up. Zeus Amy Bertha Clare Yancey Bertha Amy Clare Xavier Amy Bertha Clare Clare Xavier Yancey Zeus Bertha Xavier Yancey Zeus Amy Yancey Xavier Zeus 1 st 2nd 3rd 1 st 2nd 3rd favorite least favorite favorite least favorite Men’s Preference Profile Women’s Preference Profile
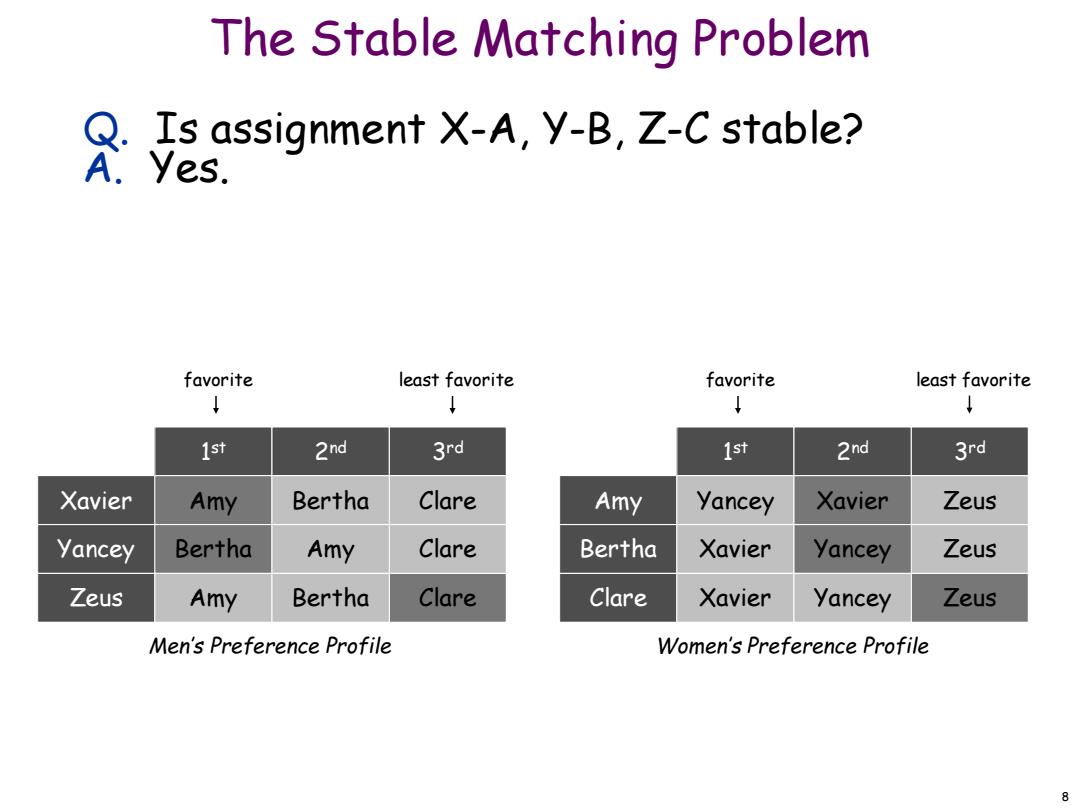
The Stable Matching Problem Q.Is assignment X-A,Y-B,Z-C stable? A.Yes. favorite least favorite favorite least favorite 1st 2nd 3rd 1st 2nd 3rd Xavier Amy Bertha Clare Amy Yancey Xavier Zeus Yancey Bertha Amy Clare Bertha Xavier Yancey Zeus Zeus Amy Bertha Clare Clare Xavier Yancey Zeus Men's Preference Profile Women's Preference Profile 8
8 The Stable Matching Problem Q. Is assignment X-A, Y-B, Z-C stable? A. Yes. Zeus Amy Bertha Clare Yancey Bertha Amy Clare Xavier Amy Bertha Clare Clare Xavier Yancey Zeus Bertha Xavier Yancey Zeus Amy Yancey Xavier Zeus 1 st 2nd 3rd 1 st 2nd 3rd favorite least favorite favorite least favorite Men’s Preference Profile Women’s Preference Profile

The Stable Roommate Problem Q.Do stable matchings always exist? A.Not obvious. Stable roommate problem. 2n people;each person ranks others from 1 to 2n-1. Assign roommate pairs so that no unstable pairs. 1st 2nd 3rd Adam B A-B,C-D三B-C unstable Bob C A-C,B-D A-B unstable A-D,B-C A-C unstable Chris A B Doofus A B c Observation.Stable matchings do not always exist for stable roommate problem. 9
9 The Stable Roommate Problem Q. Do stable matchings always exist? A. Not obvious. Stable roommate problem. 2n people; each person ranks others from 1 to 2n-1. Assign roommate pairs so that no unstable pairs. Observation. Stable matchings do not always exist for stable roommate problem. B Bob Chris Adam C A B D D Doofus A B C D C A 1 st 2nd 3rd A-B, C-D B-C unstable A-C, B-D A-B unstable A-D, B-C A-C unstable

The Propose-And-Reject Algorithm Propose-and-reject algorithm.[Gale-Shapley 1962]Intuitive method that guarantees to find a stable matching. Initialize each person to be free. while (some man is free and hasn't proposed to every woman){ Choose such a man m w 1st woman on m's list to whom m has not yet proposed if (w is free) assign m and w to be engaged else if (w prefers m to her fiance m') assign m and w to be engaged,and m'to be free else w rejects m 0
Propose-and-reject algorithm. [Gale-Shapley 1962] Intuitive method that guarantees to find a stable matching. 10 The Propose-And-Reject Algorithm Initialize each person to be free. while (some man is free and hasn't proposed to every woman) { Choose such a man m w = 1st woman on m's list to whom m has not yet proposed if (w is free) assign m and w to be engaged else if (w prefers m to her fiancé m') assign m and w to be engaged, and m' to be free else w rejects m }

Proof of Correctness:Termination Observation 1.Men propose to women in decreasing order of preference. Observation 2.Once a woman is matched,she never becomes unmatched;she only "trades up.' Claim.Algorithm terminates after at most n2 iterations of while loop. Pf.Each time through the while loop a man proposes to a new woman.There are only n2 possible proposals. 1st 2nd 3rd 4th 5th 1st 2nd 3rd 4th 5th Victor A B D E Amy W Wyatt B E Bertha Xavier E Clare Yancey B C E Diane Zeus B D E Erika W X Z n(n-1)+1 proposals required 11
11 Proof of Correctness: Termination Observation 1. Men propose to women in decreasing order of preference. Observation 2. Once a woman is matched, she never becomes unmatched; she only "trades up." Claim. Algorithm terminates after at most n2 iterations of while loop. Pf. Each time through the while loop a man proposes to a new woman. There are only n2 possible proposals. ▪ Wyatt Victor 1 st A B 2nd C D 3rd C B Zeus A Yancey Xavier C D A B B A D C 4th E E 5th A D E E D C B E Bertha Amy 1 st W X 2nd Y Z 3rd Y X Erika V Diane Clare Y Z V W W V Z X 4th V W 5th V Z X Y Y X W Z n(n-1) + 1 proposals required