《高等数学》课程教学资源（PPT课件）第七章 微分方程 7-3 第三节 齐次方程

第三节齐次方程1齐次方程可化为齐次型的方程■小结思考题

第三节 齐次方程 n 齐次方程 n 可化为齐次型的方程 n 小结 思考题

齐次方程dy的形式,如果一阶微分方程可以写成0-dxX则称之为齐次方程dydu作变量代换u=，即 =ux,=u+xdxdx一代入du+u= g(u)jx即得到u满足的方程dx

如果一阶微分方程可以写成        x y g x y d d 齐次方程.即 y  ux, 得到 u 满足的方程 ( ). d d u g u x u 即 x   的形式, , x y 作变量代换u    x y d d 代入 则称之为 u x x u d d  一 、 齐次方程

du g(u)-u可分离变量的方程dxxdudx分离变量两边积分，g(u)-ux求出通解后，用代替u.x就得到原方程的通解

可分离变量的方程 , ( ) d d x g u u x u   x x g u u u d ( ) d   分离变量 两边积分, 求出通解后, u. x y 用 代替 就得到原方程的通解

dyygdx例1 解方程xydx-(x2-y2)dy =0xydyxyx齐次方程解 将方程写为2dxxVxdydu令u=，则y=iuxXdxXdxduuU方程变为u＋x即du=dxdx1xU积分得口力离变量方程1+C=12uuX

例1 解方程 解 将方程写为 2 2 d d x y xy x y   齐次方程 , x y 令u  则 y  ux, x u u x x y d d d d   方程变为 2 d 1 d u u x u u x    即 x x u u u d 1 d 1 3 2   积分得 u x C u   ln  ln  2 1 2 2 1         x y x y 可分离变量方程 u u x y u         x y g x y d d ( ) 0 2 2 xydx  x  y dy 

例2探照灯反射镜的设计在xOy平面上有一曲线L,曲线L绕x轴旋转一周形成一旋转曲面.假设由O点发出的光线经此旋转曲面形状的凹镜反射后都与x轴平行（探照灯内的T凹镜就是这样的),求曲线L的方程y解如图，设0点发出的某条MAαS光线经L上一点M(x,y)反射后是一条与x轴平行的直线MSα文设过点M的切线ATA0x由题意与x轴的倾角是α.ZSMT = α

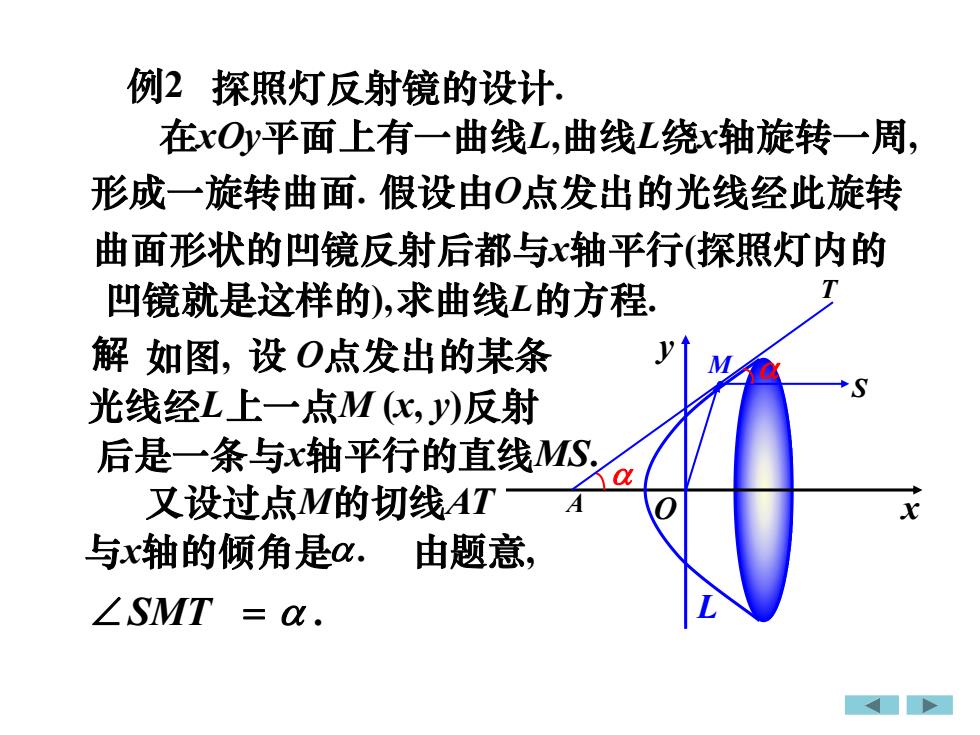
例2 探照灯反射镜的设计. 在xOy平面上有一曲线L,曲线L绕x轴旋转一周, 形成一旋转曲面. 假设由O点发出的光线经此旋转 曲面形状的凹镜反射后都与x轴平行(探照灯内的 凹镜就是这样的),求曲线L的方程. 解 如图, 设 O点发出的某条 M L 光线经L上一点M (x, y)反射 后是一条与x轴平行的直线MS. 又设过点M的切线AT 与x轴的倾角是. 由题意,  SMT   . x y O  T A S 

T入射角三反射角另一方面yMAαSZ OMA是入射角的余角，R是反射角的余角，ZSMTαA0PNx于是由光学中的反射定律有 ZOMA = ZSMT=α，1从而AO=OM，但DAO = AP-OP= PMcotα-OP:X而oM = /x? + y?.于是得微分方程2-x=x2+，即ydx = (x +/x? + y)dy一V齐次方程

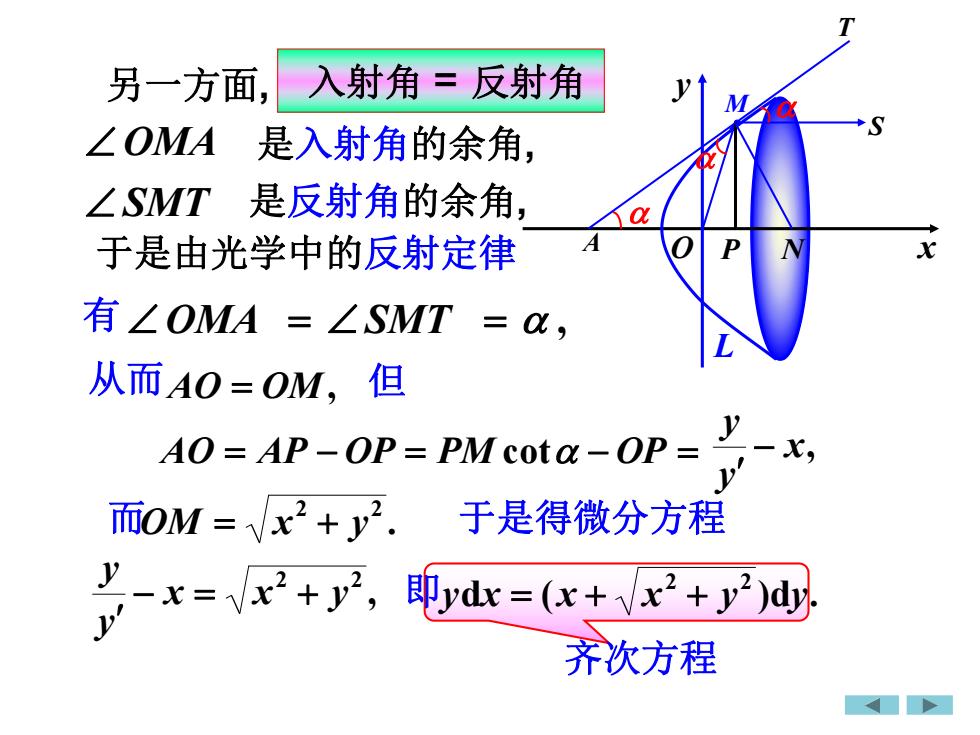
另一方面,  OMA 是入射角的余角,  SMT 是反射角的余角, 于是由光学中的反射定律 有  OMA   SMT   , 从而AO  OM, 但 AO  AP  OP  PM cot  OP  而 . 2 2 OM  x  y 于是得微分方程 , 2 2 x x y y y     即 d ( )d . 2 2 y x  x  x  y y M L x y O  T A S   P N x, y y   入射角 = 反射角 齐次方程

ydx=(x+x+y)dy为方便求解视v为自变量,x为未知函数令=，则x = yv, 有 dx = vdy + ydy,代入上式得 j(vdy+ ydv)=(yv+I y/ Vv2 +1)dy由曲线L的对称性，不妨设y>0,上式为y(vdy + ydv) = y(v+ Vv? +1)dy可分离变量的方程ydv= V2 + 1dy化简得dvdy分离变量V~+1y

为方便求解, ydx (x x y )dy 2 2    视y为自变量, x为未知函数, , y x 令v  则x  yv, 有dx  vdy  ydv, 代入上式得 ( d d ) ( | | 1)d . 2 y v y  y v  yv y v  y 由曲线L的对称性, 不妨设y > 0,上式为 ( d d ) ( 1)d , 2 y v y  y v  y v  v  y 化简得 d 1d , 2 y v  v  y . d 1 d 2 y y v v   分离变量 可分离变量的方程

dydy两边积分Vv? +1J得In(v + Vv2 + 1) = In y- InC2即v+y由上式可得v+1.VCL2yv即12c以v=二代入上式,得J2=2Cx+1这就是曲线L的方程,它是以x轴为对称轴，焦点在原点的抛物线

. d 1 d 2 y y v v   两边积分 得 ln( 1) ln ln , 2 v  v   y  C 即 1 . 2 C y v  v   由上式可得 1, 2 2          v v C y 即 1, 2 2 2   C yv C y 以 y x v  代入上式,得 . 2 2 2         C y C x 这就是曲线L的方程,它是以x轴为对称轴,焦点 在原点的抛物线

可化为齐次型的方程二、dyx+y+4dxx-y-6例3 求解15dy(y +5) +(x -1)解因方程可变形为dx-(y +5) +(x -1令y+5=(x-1)u则y"=(x -1)u' +u,1+u?代入方程，得(x-1)u'1-udx1-u分离变量,得du1+u积分得arctanuIn(1+ u2)= In|C(x-1)2

u u x u      1 1 ( 1) 2    解 令 则y  代入方程, 1 d d 1 1 2     x x u u u 积分得arctan u ln(1 ) 2 1 2   u  ln C(x  1) 分离变量,得 因方程可变形为 y  5  ( x  1)u 得 例3 求解 ( x  1)u  u , 二、可化为齐次型的方程 1 5    x y u ( 5) ( 1) ( 5) ( 1) d d         y x y x x y 6 4      x y x y x y d d 5 y x2  

.5V+通解arctan= In|C(x -1)x-12得C=1,故所求特解为y+5In [(x -1) +(y +5)]arctanx-12

通解 1 5 arctan   x y                 2 1 5 ln 1 2 1 x y  ln C (x  1) 得 C = 1, 故所求特解为 1 5 arctan   x y [ ] 2 2 ln ( 1) ( 5) 2 1  x   y 