
第一节向量及其线性运算向量的概念向量的线性运算空间直角坐标系1利用坐标做向量的线性运算向量的模、方向角、投影■小结思考题
第一节 向量及其线性运算 ◼ 向量的概念 ◼ 向量的线性运算 ◼ 空间直角坐标系 ◼ 利用坐标做向量的线性运算 ◼ 向量的模、方向角、投影 ◼ 小结 思考题

向量的概念一、向量既有大小,又有方向的量称为向量(又称量)表示法有向线段M,M,,或a,或a.向量的大小,记作a|或IM,M,向量的模起点为原点的向量向径 (矢径)自由向量与起点无关的向量模为 1 的向量,记作 a°或 M,M,单位向量M2/零向量模为0的向量,记作0Mi
一、向量的概念 表示法 向量的模 向量的大小,记作 向量 (又称矢量). M1 M2 既有大小, 又有方向的量称为向量 向径 (矢径) 自由向量 与起点无关的向量. 起点为原点的向量. 单位向量 模为 1 的向量,记作 零向量 模为 0 的向量,记作 有向线段 M1 M2 ,或 a , | a | M1M2 或 | | M1M2 0 0 a 或 0
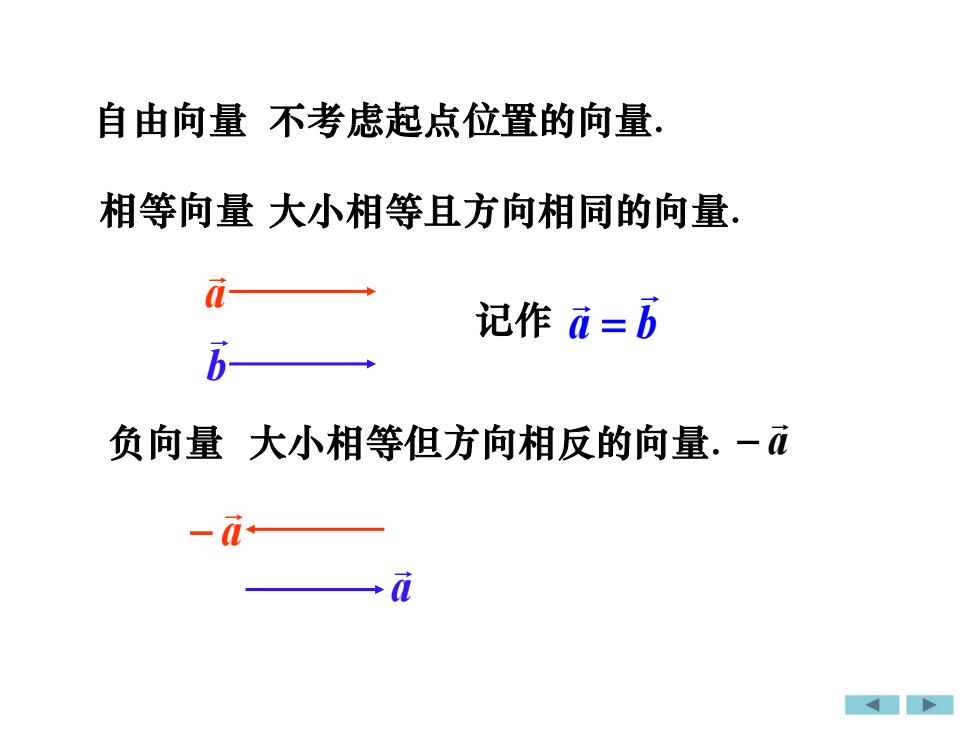
自由向量不考虑起点位置的向量相等向量大小相等耳方向相同的向量a记作 a=b-b负向量大小相等但方向相反的向量.一{a
自由向量 不考虑起点位置的向量. 相等向量 大小相等且方向相同的向量. 负向量 大小相等但方向相反的向量. a − a b a − a a b 记作 =

二、向量的线性运算1.向量的加法c(a+b)+t平行四边形法则b+t/a+ba+(b+)a+ba6三角形法则a+baaa+b-b+a运算规律交换律(a+b)+=a+(b+)=a+b+c结合律三角形法则可推广到多个向量相加
二、向量的线性运算 1. 向量的加法 三角形法则 平行四边形法则 运算规律 交换律 结合律 三角形法则可推广到多个向量相加 . b b a + b = b + a (a + b) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) (a + b) + c a a a + b a + b
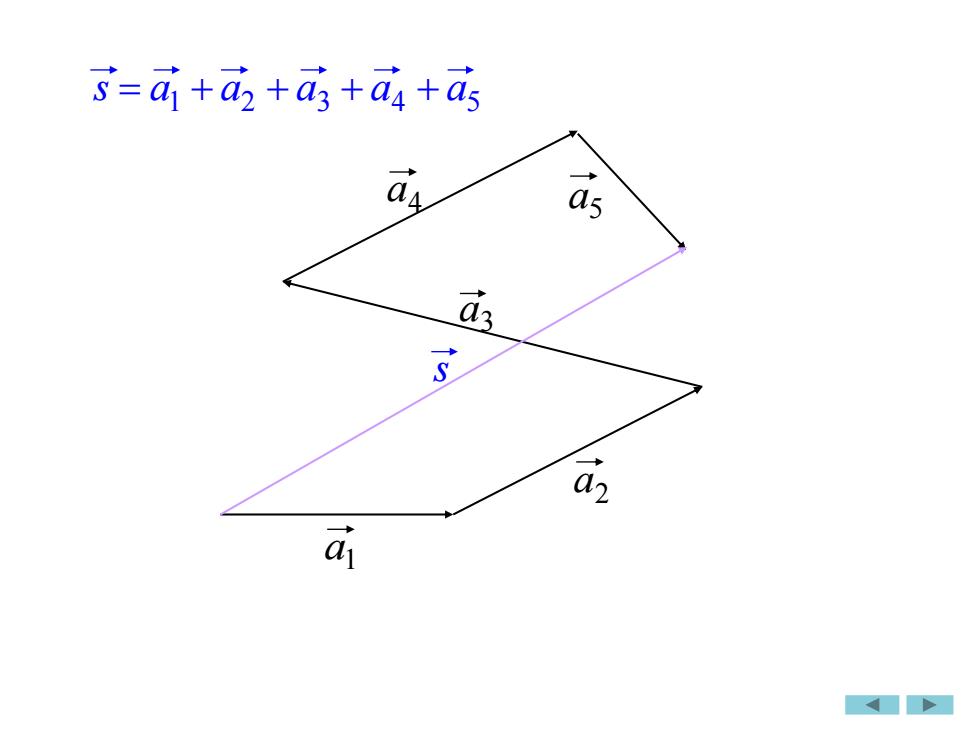
$=ai +a +a,+a +asa4a5dssa2ai
s a3 a4 a5 a2 a1 a1 a2 a3 a4 a5 s = + + + +
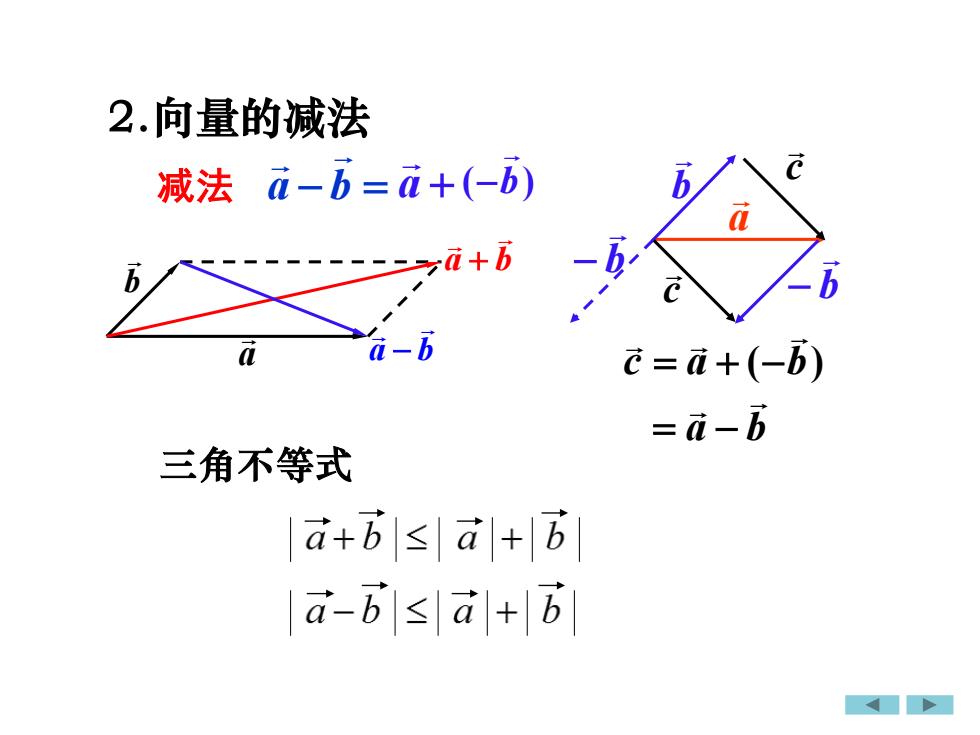
2.向量的减法ca-b=a+(-b)b减法a-b-a+b3ca-bac=a+(-b)=a-b三角不等式a+b|≤|a|+|ba-b|≤|a|+|6
减法 a − b = a b b − b c − a b c a b = − = + (− ) 2.向量的减法 ( b) a + − c a b a b + a b − 三角不等式

3.向量与数的乘法入是一个数,入与a的乘积是一个新向量,记作a规定>0,a与a同向,alal;= 0, aa = 0;0,a与a反向,a=a总之aa=|a结合律(ua)=u(aa)=aua运算律分配律(a+μ)a=aa+μaa(a+b)=aa+ab
3. 向量与数的乘法 是一个数 , a . 与 a 的乘积是一个新向量, 记作 规定 0, | a | | a |; = = 0, 0; a = 0, | a | | | | a | . = a a 与 同向, a a 与 反向, a a 总之 = 运算律 结合律 ( a) ( a) = a = 分配律 (a b) + a b = +

定理1.设a为非零向量,则allb b=aa(2为唯一实数)a,,同向时+1设a/b,取=±证“”则b与入同向,且16a|=[6]a=aa故b=aa再证数的唯一性.设又有=μa?,则(-)a=故-=0,,即=
定理1. 设 a 为非零向量 , 则 ( 为唯一实数) 证 “ ” , 取 =± 且 再证数 的唯一性 . 则 a∥b 设 a∥b , a , b 同向时 则 b 与 a 同向, 设又有 b= a , ( − )a = 0 = = b 故 b a = . 故 − = 0, 即 =

“一”已知b=a,则当=0时,=0>a//b当a>o时,a,b同向当a<o时,a,b反向例1.设M为ABCD对角线的交点,AB=a,AD=6试用a与b表示 MA,MB,MC,MD解 a+b=AC=2MC =-2MADC66-a= BD=2MD=-2MBMaBMB=-(b-a) A: MA=-(a+b)MC =(a+b)MD=(b-a)
“ ” 则 例1. 设 M 为 M A B 解 D C ABCD 对角线的交点, b a AC = −2MA BD = −2MB 已知 b= a , b=0 a , b 同向 a , b 反向 a∥b a + b = b − a = ( ) 2 1 MA = − a + b ( ) 2 1 MB = − b − a ( ) 2 1 MC = a + b ( ) 2 1 MD = b − a 试用 a 与 b 表示 MA MB MC MD , , , . 当 = 0 时, 当 0 时, 当 0 时

选择题设向量a,砭互相平行,但是方向相反,则当lab>0 时,必有(A)(A)la+b=a|-lbl; (B)la+bal-lbl;(C)la+bj错向量不能比较大小,只有模才能比较大小,0(2)a ± 0时,,"=1. 错,没有定义向量的除法,a
下列命题是否正确 错 , 错, (1) 2i j (2) 0 , = 1. a a a 时 选择题 设向量 a b 互相平行,但是方向相反,则当 , | a || b | 0 (A)| a b | | a | | b |; + = − (D)| a b | | a | | b | . + = + A 没有定义向量的除法. 向量不能比较大小, 只有模才能比较大小. 时,必有( ) (B)| a b | | a | | b |; + − (C)| a b | | a | | b |; + −