
第五节对坐标的曲面积分surface integral预备知识概念的引入概念与性质对坐标的曲面积分的计算法两类曲面积分之间的联系小结
小结 预备知识 概念的引入 概念与性质 对坐标的曲面积分的计算法 两类曲面积分之间的联系 surface integral 第五节 对坐标的曲面积分

对尘标的曲面积分预备知识一、如流体从曲面的这一侧1.有向曲面流向另一侧的流量问题等通常光滑曲面都有两侧观察以下曲面的侧(假设曲面是光滑的曲面分上侧和下侧曲面分内侧和外侧
观察以下曲面的侧 曲面分上侧和下侧 曲面分内侧和外侧 1.有向曲面 通常光滑曲面都有两侧. 如流体从曲面的这一侧 流向另一侧的流量问题等. (假设曲面是光滑的) 对坐标的曲面积分 一、预备知识
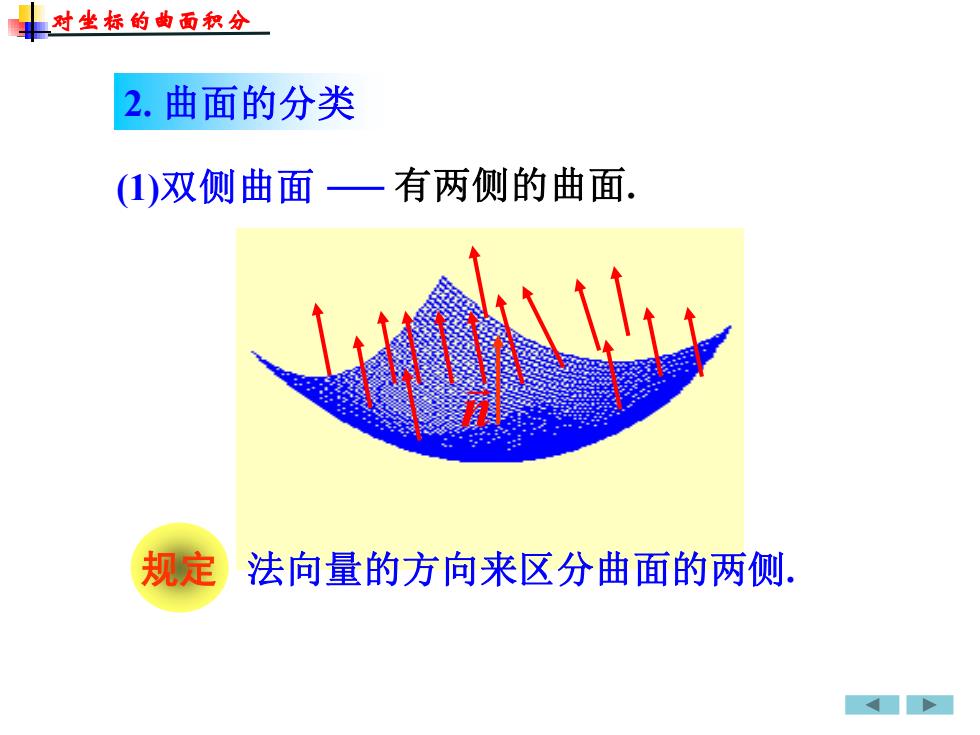
对生标的曲面积分2.曲面的分类(1)双侧曲面一有两侧的曲面.规定法向量的方向来区分曲面的两侧
n 有两侧的曲面. 规定 (1)双侧曲面 2. 曲面的分类 法向量的方向来区分曲面的两侧. 对坐标的曲面积分

对生标的曲面积分Mobius(1790--1868)19世纪德国数学家(2) 单侧曲面一莫比乌斯(Mobius)带它是由一张长方形纸条ABCD,扭转一下将A、D粘在一起,B、C粘在一起形成的环行带.小毛虫在莫比乌斯带上,不通过边界可以爬到任何一点去。这在双侧曲面上是不能实现的决定了侧的曲面称为有向曲面
(2) 单侧曲面 莫比乌斯(Mobius)带. B、C 粘在一起形成的环 不通过边界可以 这在双侧曲面上是不能实现的. 决定了侧的曲面称为 它是由一张长方形纸条ABCD,扭转一下, 将A、D粘在一起, 行带. 小毛虫在莫比乌斯带上, 爬到任何一点去. 有向曲面. 对坐标的曲面积分 Mobius(1790-1868) 19世纪德国数学家

对尘标的曲面积分3.有向曲面在坐标面上的投影设是有向曲面.在有向曲面上取一小块曲面AS,△S在xOy面上的投影(△S)x,为(△)xy当cos>0时当cos0时(△S)x, =} -(A0)x0当cos=0时其中(△α)x,表示投影区域的面积.假定△S上各点处的法向量与z轴的夹角的余弦cos有相同的符号。y恰好等于△S与坐标面xOv的二面角
3. 有向曲面在坐标面上的投影 其中( ) 表示投影区域的面积. xy 设Σ是有向曲面. 曲面S, S在xOy面上的投影(S) x y为 (S) xy = ( ) xy 当cos 0时 − ( ) xy 当cos 0时 0 当cos = 0时 恰好等于 S 与坐标面xOy的二面角. 假定 cos S 的余弦 上各点处的法向量与 z轴的夹角 有相同的符号. 在有向曲面 上 取一小块 对坐标的曲面积分

对生标的曲面积分△S在xOy面上的投影(△S)xy,实际上就是AS在xOy面上的投影区域的面积附以一定的正负号。类似地,可定义△S在vOz面及zOx面的投影:(△S) yz, (AS)z→α,β恰好等于△S与坐标面yOz、zOx的二面角
类似地,可定义 S 在yOz面及zOx面的投影: ( ) , S yz , ( ) , S 在xOy面上的投影 S xy S 在xOy面上的投影区域的面积附以一定的 实际上就是 正负号. S zx ( ) 恰好等于S与坐标面yOz、zOx 的二面角. 对坐标的曲面积分
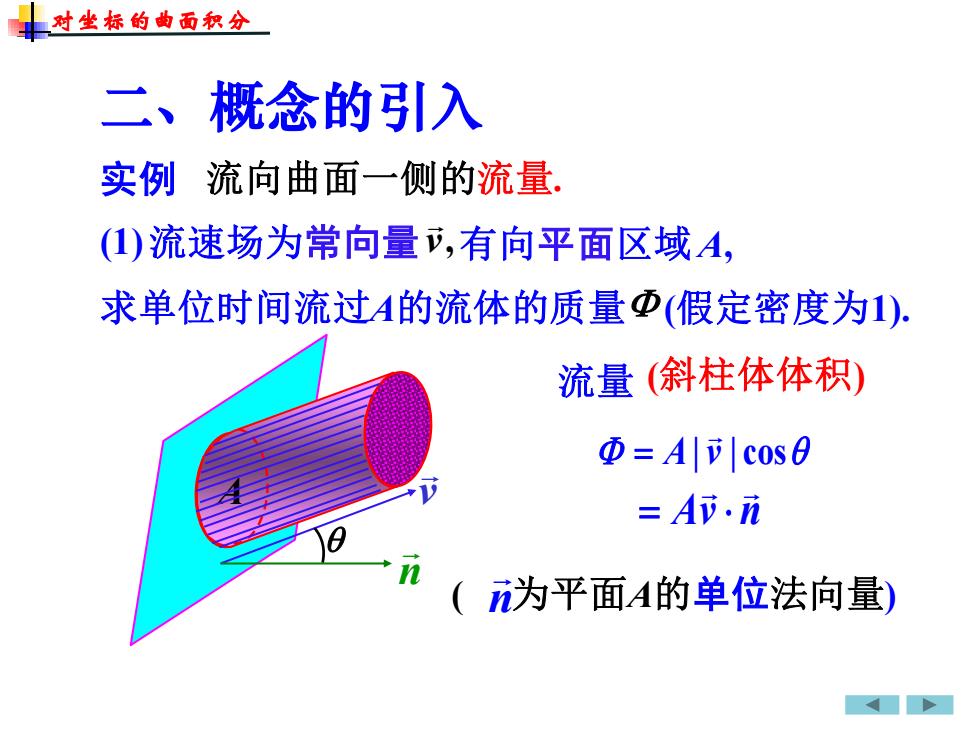
对生标的曲面积分概念的引入二、实例流向曲面一侧的流量(1)流速场为常向量,有向平面区域A.求单位时间流过A的流体的质量Φ(假定密度为1)(斜柱体体积)流量@= A||cos V= Ai.n0nn为平面A的单位法向量
流向曲面一侧的流量. v A| v | cos = 流量 实例 ( n 为平面A的单位法向量) (斜柱体体积) Av n = (1)流速场为常向量 v, 有向平面区域 A, 求单位时间流过A的流体的质量 (假定密度为1). 对坐标的曲面积分 二、概念的引入 A n

对尘标的曲面积分当不是常量,向曲面(2)设稳定流动的假定密度为1)不可压缩流体的速度场由流体的密度与速度z)k均不随时间而变化i(x, y,z) = P(x, y,z)给出,Z是速度场中的一片有向曲面,函数P(x, y,z), Q(x, y,z), R(x, y,z)都在上连续,求在单位时间内流向指定侧的流体的质量Φ
(2) 设稳定流动的不可压缩流体 v x y z P x y z i Q x y z j R x y z k ( , , ) = ( , , ) + ( , , ) + ( , , ) 给出, 函数 P(x, y,z), Q(x, y,z), R(x, y,z) 都在上连续, 流体的密度与速度 均不随时间而变化 (假定密度为1) 的速度场由 v 当 不是常量, 有向 曲面 求在单位 时间内流向 指定侧的 流体的质量 . 是速度场中的一片有向曲面, 对坐标的曲面积分
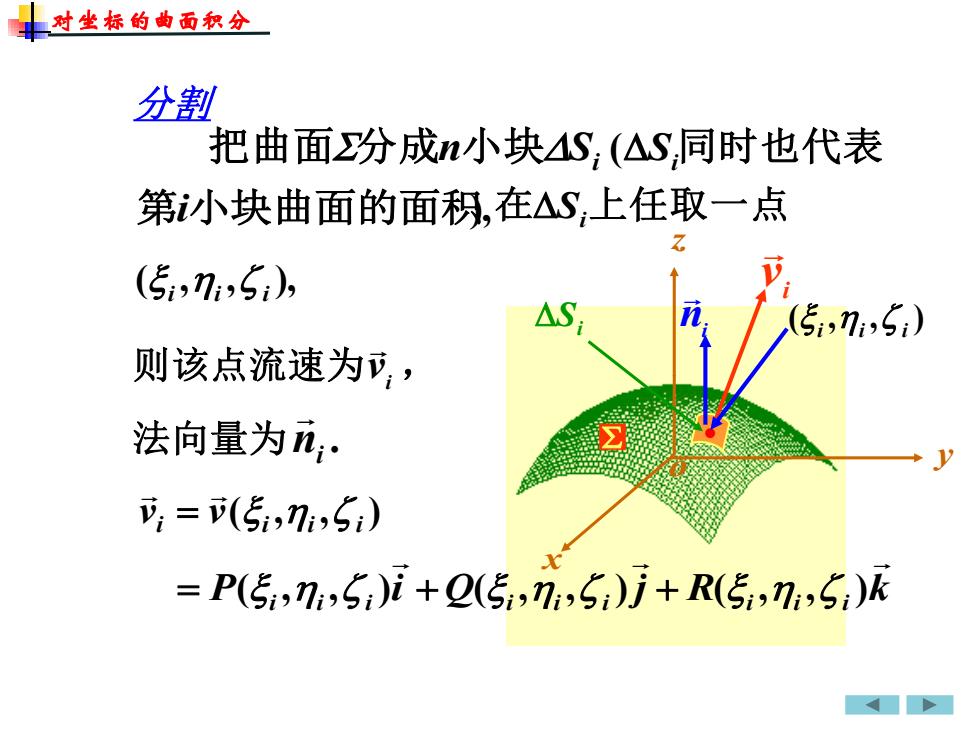
对尘标的曲面积分分割把曲面汾成n小块AS(△S,同时也代表第小块曲面的面积,在△S,上任取一点TV(Si,Ni,S,),nAS(5,,ni,S)福则该点流速为,,冈法向量为n.., = v(Si,Ni,S)= P(5,ni,S)i +Q(5i,n,S)j+ R(5,n,S)k
x y z o Si i v ni 分割 则该点流速为 vi , 法向量为 . ni • ( , , ) i i i 把曲面分成n小块Si (Si 同时也代表 第i小块曲面的面积),在Si 上任取一点 ( , , ), i i i ( , , ) i i i i v v = P i i i i Q i i i j R i i i k = ( , , ) + ( , , ) + ( , , ) 对坐标的曲面积分

对尘标的曲面积分常向量.有向平面@=Alilcose= Av·n该点处曲面的单位法向量n, = cosα,i + cos β,j+ cos,k取近似通过入S,流向指定侧的流量的近似值为AΦ, ~v, Icos(v,n,)AS, = v, n,As高底(i = 1,2, .", n)求和通过Z流向指定侧的流量@~Ev.n,ASi=1
常向量,有向平面 i 求和 = n i i ni Si v 1 取近似 该点处曲面Σ的单位法向量 通过Si流向指定侧的流量的近似值为 i ni Si = v 高 底 (i = 1,2, ,n). Si A| v | cos = Av n = 对坐标的曲面积分 通过Σ流向指定侧的流量 ni i i i j ik = cos + cos + cos | | cos( , ) i i ni v v