
第六节高斯公式通量与散度高斯公式■简单的应用物理意义一通量与散度函数小结思考题
第六节 高斯公式 通量与散度 ◼ 高斯公式 ◼ 简单的应用 ◼ 物理意义—通量与散度 ◼ 函数 ◼ 小结 思考题

高斯(Gauss)公式定理1设空间闭区域2由分片光滑的闭曲面乙所围成,乙的方向取外侧,函数P,Q,R在则有2上有连续的一阶偏导数,aRapa0Jdxdydz+SDF.CaxOzay=$f, Pd ydz+Qdzdx+ Rdxd y(Gauss公式)
一、高斯(Gauss)公式 定理1 设空间闭区域由分片光滑的闭曲 上有连续的一阶偏导数, d d d d d d P y z Q z x R x y = + + 面所围成,的方向取外侧, 函数P, Q, R在 则有 (Gauss公式)

aR下面先证:J.2$f, Rdxdydxdydz=N证明设Q:z,(x,y)<z(x,y)≤zz(x, y), (x,y)eDx为XY型区域Z=Z,UZ,UE3,(取下侧)Z, : z = z,(x, y),E, : z = z2(x,y),(取上侧)匕,:母线平行于z轴的柱面(取外侧)则
d d d R x y z z d d R x y = 下面先证: 证明 设 1 2 3 为XY型区域, = , 1 1 = : ( , ), z z x y 2 2 = : ( , ), z z x y 3 : 母线平行于z轴的柱面. (取外侧) (取下侧) (取上侧) 则
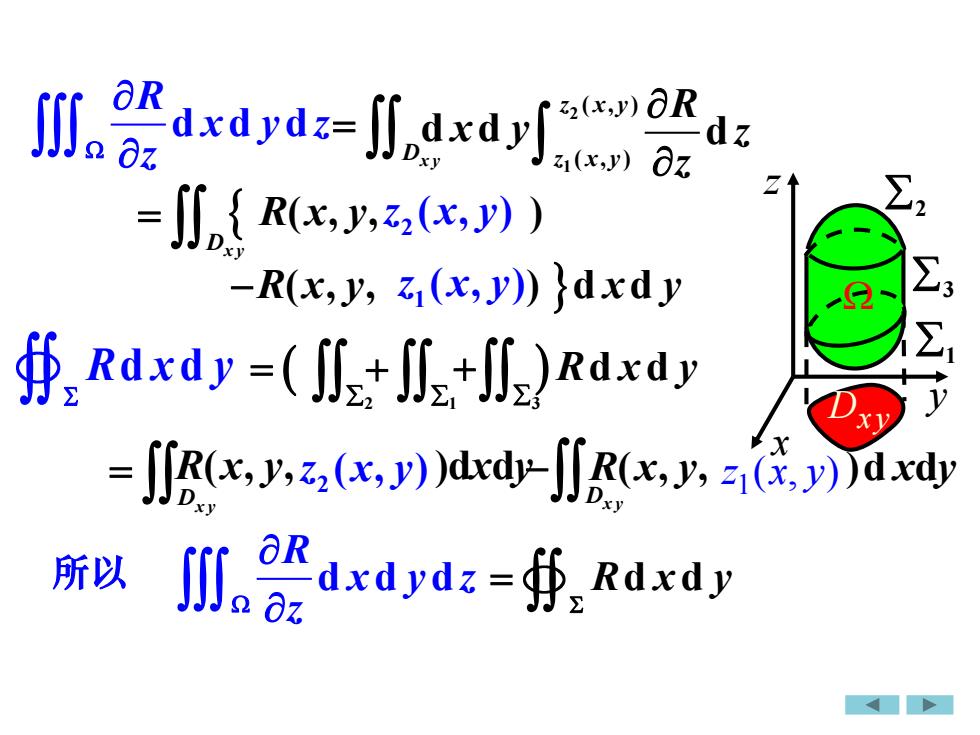
aRz(x,y) ORI.2dxdydz=dxdjdzDxyOzz(x,y)Z1ZJJD( R(x,y,z2(x, ) )Z3-R(x,y, zi(x,y) /dxd y2Z折,Rdxdy =( JJ,+ J,+J2)Rdxdy>yDxy[IR(x, y,z,(x, y))dxdyR(x, y, zi(x, y))d xdyDaRI所以dxdydz=f, Rdxdy2 Oz.-
2 3 1 z y x Dxy R x y ( , , ) −R x y x y ( , , ) d d 2 1 ( , ) ( , ) d z x y z x y R z z Dx y = 2 z x y ( , ) 1 z x y ( , ) d d R x y Dx y = ( 2 = d d d R x y z z d dx y 1 + 3 + ) R x y d d R x y x y ( , , )d d Dx y − Dx y = 2 z x y ( , ) R x y x y ( , , )d d ( , ) 1 z x y 所以 d d d R x y z z d d R x y =

则可引进辅助面若Q不是XY-型区域将其分割成若干个XY-型区域在辅助面正反两侧面积分正负抵消故上式仍成立apJIdxdydz =$, Pd ydz类似可证oxQ0.%dxdydz = $f,Qdzdx三式相加,即得所证Gauss公式:aRaodp(%xdxd ydzazaxay-$f,Pd ydz+Qdzdx+ Rdxdy>
若不是XY–型区域, 则可引进辅助面 将其分割成若干个XY–型区域, 故上式仍成立. 在辅助面 正反两侧面积分正负抵消, 类似可证 d d d Q x y z y d d d d d d P y z Q z x R x y = + + ( )d d d P Q R x y z x y z + + d d Q z x = d d d P x y z x d d P y z = 三式相加, 即得所证Gauss公式:

由两类曲面积分之间的关系知高斯公式的另一种形式:apaRaQ5)dyazaxdQ=(Pcos a +Qcos β+ Rcos )ds.ZGauss公式的实质表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系
Gauss公式的实质 表达了空间闭区域上的三重积分与其边界曲 面上的曲面积分之间的关系. ( ) ( cos cos cos ) . P Q R dv x y z P Q R dS + + = + + 由两类曲面积分之间的关系知高斯公式的另一 种形式:

二、简单的应用使用Gauss公式时应注意:1.P,Q,R是对什么变量求偏导数;2.是否满足高斯公式的条件;3.Z是取闭曲面的外侧
使用Gauss公式时应注意: 1.P,Q,R是对什么变量求偏导数; 2.是否满足高斯公式的条件; 3.Σ是取闭曲面的外侧. 二、简单的应用

f,(x-y)dxd y+(y-z)xd ydz例1用Gauss公式计算其中为柱面x2 + v2 =1及平面z=0,z=3所围空间闭域2的整个边界曲面的外侧分析这里为闭域,可直接用Gauss公式将其OL化为三重积分,P=(y一z)x,1xQ=0, R=x-y
例1 用Gauss公式计算 其中为柱面 闭域的整个边界曲面的外侧. 分析 这里为闭域,可直接用Gauss公式将其 化为三重积分, x 3 o z 1 y P y z x = − ( ) , Q = 0, R x y = − 及平面z=0, z=3所 围空间

解JJ, (y-z)dxdydz(用柱坐标)原式=拉JJ,(rsino-z)rdrdedz9元" def,rdrf(rsin-z)dz=2思考夫若之改为内侧,结果有何变化?若Z为圆柱侧面(取外侧),如何计算?
思考 若改为内侧,结果有何变化? 若为圆柱侧面(取外侧),如何计算? ( sin ) d d d r z r r z = − 2 1 3 0 0 0 d d ( sin )d r r r z z = − 9 2 = − 原式 = ( )d d d y z x y z − 解 (用柱坐标)

例2利用Gauss公式计算积分I = J],(x cosα+ y° cos β+z cosy)ds7x2+2=z2介于z=0及eh其中Z为锥面Zz=h之间部分的下侧1分析这里乙不是闭域,需作辅助面:AEr:z= h, (x,y)eDxy :x?+y<h记,Z,月取上侧,所围区域为2,则在,上α=β=,=0
例2 利用Gauss 公式计算积分 其中为锥面 2 2 2 x y z + = h 分析 这里不是闭域,需作辅助面: 1 = : , z h 2 2 2 ( , ) : , x y x y D x y h + 取上侧, 1 2 , 0 在 = = = 上 介于z=0及 z= h之间部分的下侧. 1 , o z y x 1 h 所围区域为, 则 记