山东理工大学：《内燃机设计》课程教学资源（PPT讲稿）第三章 内燃机零件的强度计算基础

第三章内燃机零件的强度计算基础 3-1内燃机零件的机械负荷和热负荷 内燃机上的零件通常是在内燃机总体尺寸限定的情况 下进行设计的，零件的强度计算是设计中的重要环节，它 彝翔贪盘薰然墾艺务鑫家猴籍的重侯滨，世是远 为了对零件进行强度计算，必须提供零件所承受负荷 的性质与大小。，对肉燃机来说，某些零件不仅承受机械负 荷而且还承受热负荷。 因此这种零件上的应力是机械应力和热应力的叠加。 对于一些重要的零件，除了进行强度计算外，还要进行强 度模拟实验。 目前，由于在多数情况下内燃机零件的强度计算是在 弹性变形的范围内进行的，所以仅应用材料力学提供的概 和方法是不够的.必须应角弹惟力学的概念和公式。如 窠考蓊蒸态男的还姜甯传熟攀率碧关鐘论。公 有限元法是目前零件强度计其中最广泛采用的方法

第三章 内燃机零件的强度计算基础 3-1内燃机零件的机械负荷和热负荷 内燃机上的零件通常是在内燃机总体尺寸限定的情况 下进行设计的，零件的强度计算是设计中的重要环节，它 是确定零件形状和尺寸参数是否合理的重要依据，也是选 择材料以及热处理工艺等的基本依据。 为了对零件进行强度计算，必须提供零件所承受负荷 的性质与大小。对内燃机来说，某些零件不仅承受机械负 荷而且还承受热负荷。 因此这种零件上的应力是机械应力和热应力的叠加。 对于一些重要的零件，除了进行强度计算外，还要进行强 度模拟实验。 目前，由于在多数情况下内燃机零件的强度计算是在 弹性变形的范围内进行的，所以仅应用材料力学提供的概 念和方法是不够的．必须应用弹性力学的概念和公式。如 果考虑到热应力，还要应用传热学中的有关理论。 有限元法是目前零件强度计其中最广泛采用的方法

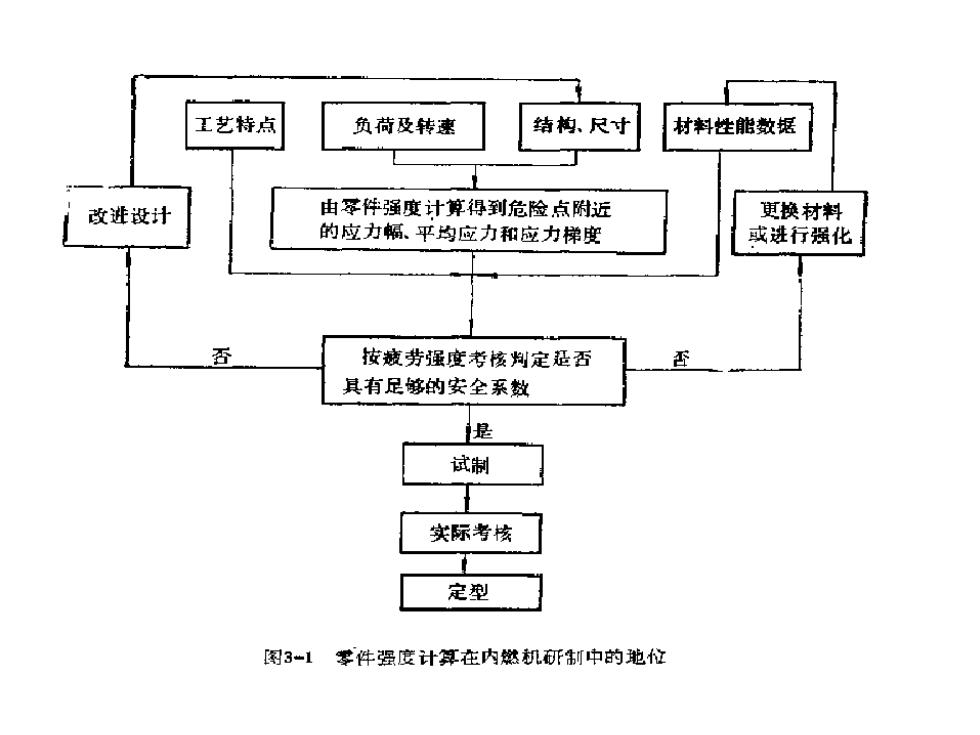
工艺特点 负荷及转速 结构、尺寸 材料性能数据 改进设计 由零件强度计算得到危险点附近 更换材料 的应力幅、平均应力和应力梯度 或进行强化 否 按疲劳强度考核判定延否 其有足够的安全系数 是 试制 实际考核 定型 图3一1零件强度计算在内燃机研制中的驰位

3-2弹性力学基本公式 描述均匀、连续、各向同 性弹性体的位移、应变、应力 间的互相关系以及它们与外负 荷之间的关系

3-2 弹性力学基本公式 描述均匀、连续、各向同 性弹性体的位移、应变、应力 间的互相关系以及它们与外负 荷之间的关系

、一点应力状态 ·九个应力分量 ·正应力 剪应力：，第一个脚标表示剪应力作 用截面的法线方向，第二个脚标表 示剪应力的指向。 剪应力互等定理 九个应力分量中只有六个是不同的。x 应力的正负号：，正应力以拉为正， Ox 压为负。剪应力，若其作用截面的 外法线与某一坐标轴方向相同，二其 应力就以沿坐标轴的正方向为正， 羹标地要反的養翳 {o}= 6 应力就苡沿坐标轴货方尚为正，沿 坐标轴正方向为负

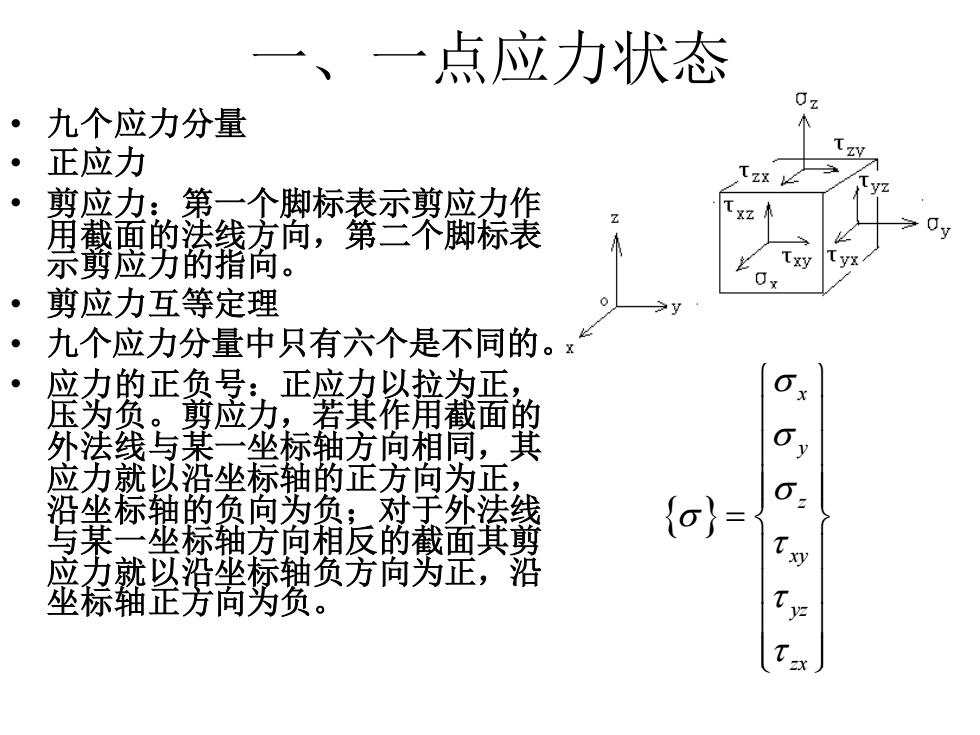
一、一点应力状态 • 九个应力分量 • 正应力 • 剪应力：第一个脚标表示剪应力作 用截面的法线方向，第二个脚标表 示剪应力的指向。 • 剪应力互等定理 • 九个应力分量中只有六个是不同的。 • 应力的正负号：正应力以拉为正， 压为负。剪应力，若其作用截面的 外法线与某一坐标轴方向相同，其 应力就以沿坐标轴的正方向为正， 沿坐标轴的负向为负；对于外法线 与某一坐标轴方向相反的截面其剪 应力就以沿坐标轴负方向为正，沿 坐标轴正方向为负。   x y z xy yz zx                =            

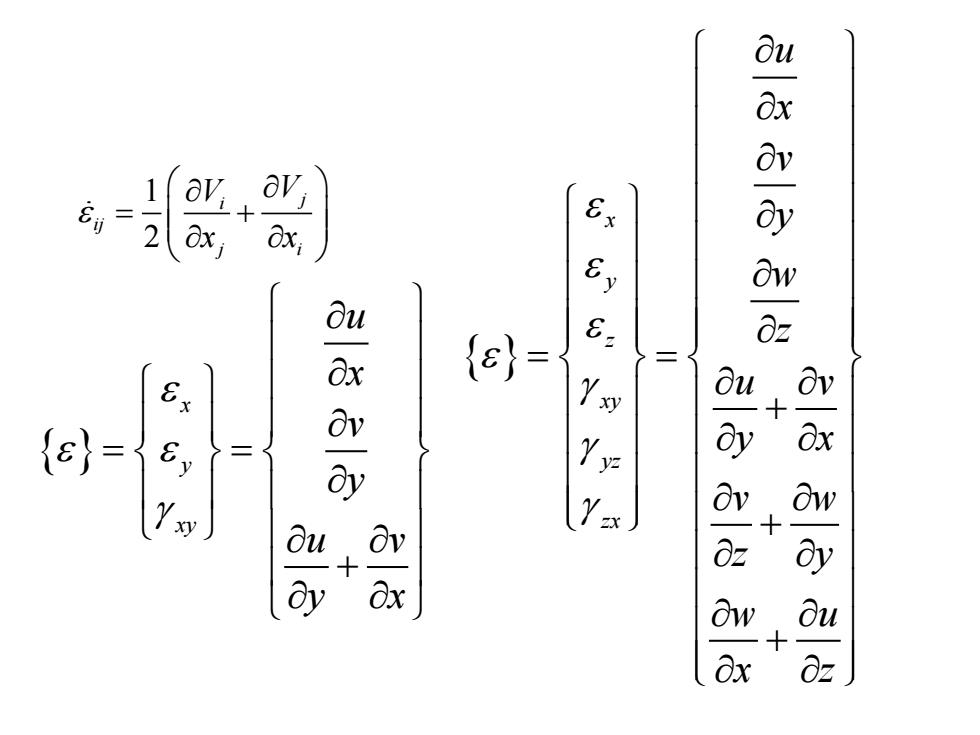
二、应变位移方程 。 弹性体沿着x、y、2方向的变形，可以分别用u、y、w三 个位移分量表示，在小变形的情况下，应变位移关系是线 性的。 ·任一点的应变状态→九个应变分量，即三个正应变和六个 剪应变 au ou Exx-Ex- .6-6y=a ax 2,6=8:= 8z 10+x 6w=8m=2w=20 auy 1 6== 2 =2a 1 x=Ex2- oux 2 ax

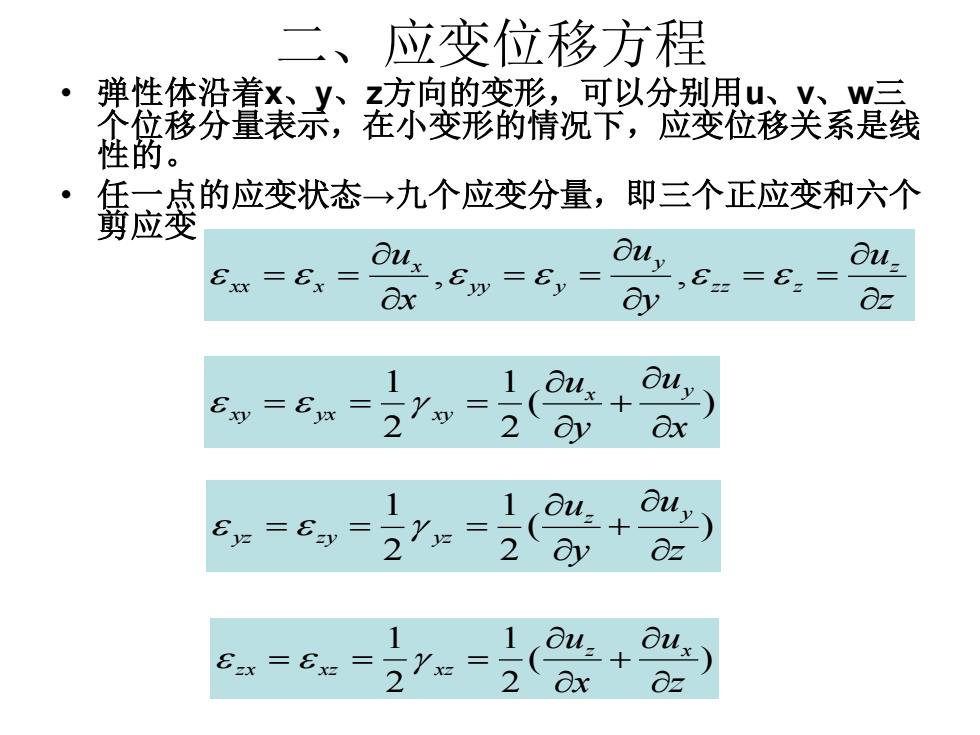
二、应变位移方程 • 弹性体沿着x、y、z方向的变形，可以分别用u、v、w三 个位移分量表示，在小变形的情况下，应变位移关系是线 性的。 • 任一点的应变状态→九个应变分量，即三个正应变和六个 剪应变 z u y u x u z z z z y yy y x xx x   = =   = =    =  = ,  ,  ( ) 2 1 2 1 x u y ux y xy yx xy   +    =  =  = ( ) 2 1 2 1 z u y uz y yz z y yz   +    =  =  = ( ) 2 1 2 1 z u x uz x z x xz xz   +    =  =  =

+器d 应变符号规定： 8 正应变或线应变 B 伸长为正，缩短为负； 剪应变或切应变(8,8,6) 夹角减小为正，增大为负： dx 图3-3微元休剪应变示意图 Yn=ga+gB≈a+B=u+ dy dx

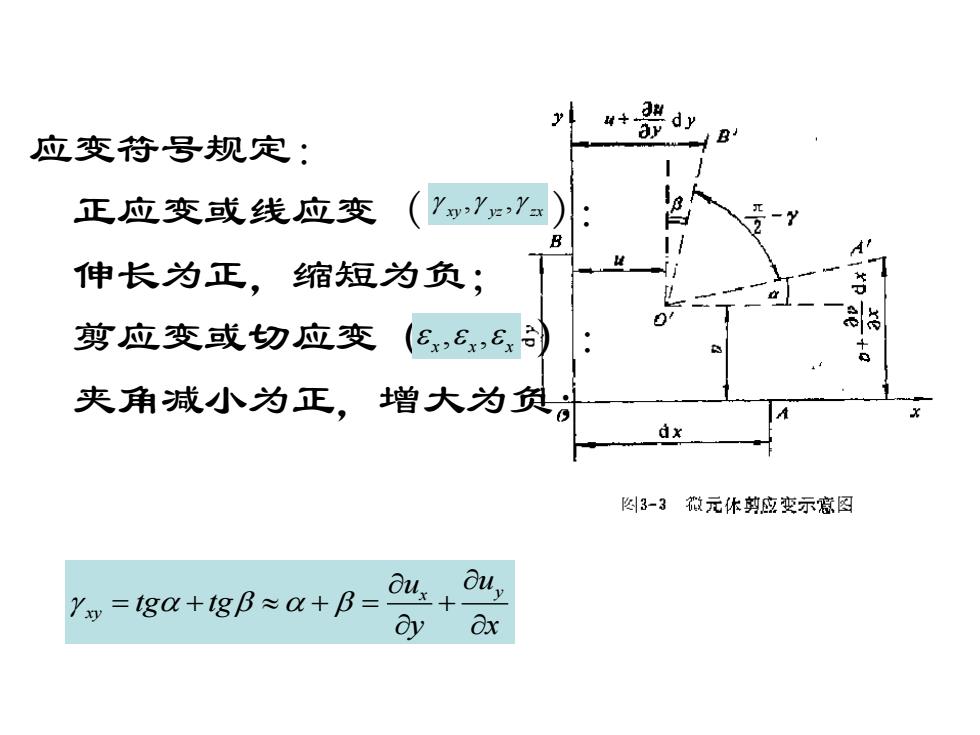
应变符号规定： 正应变或线应变 ( )： 伸长为正，缩短为负； 剪应变或切应变（ ）： 夹角减小为正，增大为负； x y xy u u tg tg y x        = +  + = +   , , xxx  , , xy yz zx 

1 Ex 2 {= {e} 。二 L

1 2 j i ij j i V V x x      = +           x y z xy yz zx u x v y w z u v y x v w z y w u x z                                          = =           +           +           +         x y xy u x v y u v y x                    = =                  +    

三、应力-应变方程 应力表示本构方程 E=2a,-o,+o,】=+0-o1 ,-4o,+a】=E【I+0o,-O] 1 E E E. lo. (a,+o,】=E[1+Wa:-O] G •E为弹性模量 •G为剪切弹性模量 Y G ·“为横向变形系数—泊松比 Yx G E G- 2(1+)

三、应力-应变方程 应力表示本构方程 1 1 [ ( )] [(1 ) ] 1 1 [ ( )] [(1 ) ] 1 1 [ ( )] [(1 ) ] x x y z x y y x z y z z x y z xy xy yz yz xz xz E E E E E E G G G                               = − + = + −  = − + = + −  = − + = + −  = = = •E为弹性模量 •G为剪切弹性模量 •  为横向变形系数——泊松比 2(1 ) E G  = +

泊松 法国数学家、物理学家和力学家

泊松 法国数学家、物理学家和力学家

应变-应力 {o}=[D]{&} 对 1-4 41 1-4 1-4 (DI= E(1-4） 1+41-2)） 0 00 1-24 称 21-4）) 0 00 1-2u 0 21-4） 0 00 1-24 21-4)

应变-应力 1 1 1 1 1 1 (1 ) [ ] 1 2 (1 )(1 2 ) 0 0 0 2(1 ) 1 2 0 0 0 0 2(1 ) 1 2 0 0 0 0 0 2(1 ) E D                    − − − − =   − + −   − − − −   − 对 称 { } [ ]{ }   = D