
第6卷第5期 智能系统学报 Vol.6 No.5 2011年10月 CAAI Transactions on Intelligent Systems 0ct.2011 doi:10.3969/j.issn.16734785.2011.05.005 差分进化算法参数控制与适应策略综述 杨振宇1,唐珂2 (1.华东师范大学计算机科学技术系,上海200241;2.中国科学技术大学计算机科学与技术学院,安徽合肥230027) 摘要:差分进化算法逐渐成为进化计算领域最流行的随机搜索算法之一,已被成功用于求解各类应用问题.差分 进化算法参数设置与其性能密切相关,因此算法参数控制与适应策略设计是目前该领域的研究热点之一,目前已涌 现出大量参数控制方案,但尚缺乏系统性的综述与分析.首先简要介绍差分进化算法的基本原理与操作,然后将目 前参数控制与适应策略分成基于经验的参数控制、参数随机化适应策略、基于统计学习的参数随机化适应策略和参 数自适应策略4类进行系统性综述,重点介绍其中的参数适应与自适应策略.此外,为分析各种参数控制与适应策 略的功效,以实值函数优化为问题背景设计了相关实验,进一步分析各种策略的效率与实用性,实验结果表明,参数 自适应控制策略是目前该领域最有效的方法之一 关键词:进化计算;差分进化;参数控制;适应策略;自适应 中图分类号:TP18;0224文献标志码:A文章编号:16734785(2011)05041509 An overview of parameter control and adaptation strategies in differential evolution algorithm YANG Zhenyu',TANG Ke2 (1.Department of Computer Science and Technology,East China Normal University,Shanghai 200241,China;2.School of Computer Science and Technology,University of Science and Technology of China,Hefei 230027,China) Abstract:Differential evolution algorithms have gradually become one of the most popular types of stochastic search algorithms in the area of evolutionary computation.They have been successfully applied to solve various problems in real-world applications.Since their performance often depends heavily on the parameter settings,the design of param- eter control and adaptation strategies is one of the current hot topics of research in differential evolution.Although nu- merous parameter control schemes have been proposed,systematic overviews and analysis are still lacking.In this pa- per,first the basic principles and operations of the differential evolution algorithm were briefly introduced,and then a detailed overview was provided on different parameter control and adaptation strategies by dividing them into the fol- lowing four classes:empirical parameter settings,randomized parameter adaptation strategies,randomized parameter adaptation strategies with statistical learning,and parameter self-adaptation strategies.The overview emphasized the latter two classes.To study the efficacy of these parameter control and adaptation strategies,experiments with the background of real-valued function optimization were conducted to compare their efficiency and practicability further. The results showed that the parameter self-adaptation is one of the most effective strategies so far. Keywords:evolutionary computation;differential evolution;parameter control;adaptation strategies;self-adaptation 差分进化(differential evolution,DE)算法la]于 优点[41,已被广泛和成功地应用于全局优化、运筹 1995年由Storn和Pice提出,是一种新颖的通过引 管理、工程设计等领域56」 入独特的差分变异模式进行迭代搜索的进化算法. 进化算法参数控制与适应一直都是进化计算领 该方法因具有简单、易实现、高效、鲁棒性强等多种 域的核心研究问题,这主要是因为该类方法的具体 流程与操作通常由算法参数控制,使得这些参数的 收稿日期:2010-1102. 基金项目:海外及港澳学者合作研究基金资助项目(61028009). 设置与算法性能息息相关).与传统进化算法类 通信作者:唐珂.E-mail:ketang@ustc.edu.cm 似,DE算法同样也具有其自身的控制参数.经典

416 智能系统学报 第6卷 DE算法具有3个主要的控制参数山:1)种群大小 表群体中的一个个体,D是目标问题的决策变量个 N;2)变异缩放因子F;3)交叉概率Pc除了种群大 数,也可以称为该问题的维数,N是群体大小.DE算 小N这个任何基于群体搜索的算法都具有的一般性 法的初始化方法与其他进化算法类似,一般是在指 参数外,研究发现DE算法性能对另外2个参数的 定搜索空间内均匀随机生成N个D维实值向量构 设置非常敏感,而且往往与具体问题相关,经验参数 成其初始群体. 设置并不总能使该算法发挥出其最高性能,而手动 1.2变异操作 参数调节费时费力,极大降低了算法的实用性.为了 给定当前群体{X1i=1,2,…,N},对其中的任 提高DE算法的性能和实用性,其参数的控制与适 意个体X,DE算法的变异操作按照式(1)生成一个 应策略设计已成为DE领域的热点研究方向,除基 对应的变异个体. 于经验的参数设置外,研究者们提出了大量更先进 V:=X,+F×(X2-Xa) (1) 的参数控制与适应策略,如参数随机化适应策 式中:X,、X,2和Xa是从当前群体中随机选择的3个 略[8]、基于统计学习的参数随机化适应策略9]、参 互不相同的个体,而且它们也不应与目标个体X:相 数自适应策略[1o]等。 同;缩放因子F是一个大于0的实常数,实验表明 针对DE算法的参数控制与适应问题,目前研 它一般应满足条件F∈(0,2],而F=0.5通常是比 究者多以他们各自的视角提出了各种不同策略,尚 较合适的设置.在具体算法实现中,由于式(1)中 缺乏对这些现存策略的综述与系统性对比分析.本 的X2和Xa是随机选择的2个个体,F取负值仅代 文对目前研究中出现的主要的参数控制与适应策略 表两者交换位置,并不违背DE算法的设计原理,因 进行综述,将它们分成如下4类进行分析:1)基于 此DE研究中也会出现将F限定在区间[-2,0)U 经验的参数控制;2)参数随机化适应策略;3)基于 (0,2]的情况 统计学习的参数随机化适应策略;4)参数自适应策 随着DE算法的发展,根据差分向量构造方式 略.除此之外,还以实值函数优化问题为背景,用具 的不同,研究者还提出其他多种算法变种,常用的有 体实验结果对比来讨论各种参数控制与适应策略的 如下几种21: 实际效果 V,=Xbet+F×(X,i-X2), 差分进化算法 V:=X:+F×(Xt-X)+F×(Xi-X2), V:=Xm+F×(X,H-X2)+F×(Xa-X4), DE的主要思想是引入一种全新的可利用当前 V:=X+F×(X2-Xa)+F×(X4-Xs) 群体中个体差异来构造变异个体的差分变异模式 根据具体应用问题的不同,这些变异模式各有优缺 相对于传统进化算法,差分变异模式是DE算法中 点,但式(1)所表示的经典方式仍然是最常用、最有 最为独特的进化操作.以经典DE算法为例,在每代 效的变异模式之一 算法迭代过程中,对于当前群体中的每个目标个体, 1.3交叉操作 算法首先随机选择2个其他个体并使它们相减构成 在完成变异操作后,DE算法将在目标个体X: 差分向量,然后将该差分向量乘以一个缩放因子F 和变异个体V:之间执行一种离散交叉操作,从而生 后加到第3个随机个体上构成变异个体,最后该变 成一个测试个体U,该离散交叉可描述如下: 异个体再经过与对应目标个体的交叉和选择操作生 U,()= [V:(j),R(0,1)PcR or j jmma; 成一个新个体进入下一代.基于上述过程并结合文 X(), otherwise. 献[1]中的描述,以下将以实值优化问题(即决策变 式中:R(0,1)是一个在(0,1)的均匀随机数发生 量为实数)为背景,具体介绍DE算法的群体表示与 器是[1,D]的一个随机整数,以确保不会出现 各种进化操作 测试个体U:完全复制X:的情况;PcR∈[0,1]是交 1.1群体表示与初始化 叉概率,用来控制在哪些决策变量上采用变异值,一 对于实值优化问题,DE算法中的群体一般表 般可设置为0.9」 示成N个D维向量: 1.4选择操作 {X|i=1,2,…,N 对于每一个测试个体U:,DE算法采用如下一 式中:实值向量X=(X(1),X(2),…,X(D))代 对一的贪心选择方式:

第5期 杨振宇,等:差分进化算法参数控制与适应策略综述 .417 rU,ffU)≤(x); 也可能具有不同需求,不存在能适用于所有目标问 X;= LX: otherwise. 题的统一固定参数设置,所以经验参数控制逐渐不 式中:代·)是目标函数(最小化问题);X:是代替 能满足DE算法在越来越广泛的应用问题上的求解 X:而进入下一代的子个体 性能要求.特别是对于特征未知的应用问题,仍然需 完成上述选择操作后,DE算法得到一个新的 要通过费时费力的手动参数调节才能找到比较合适 群体{XIi=1,2,…,N}进入下一代,从而可以迭代 的经验参数,这大大降低了DE算法的实用价值.为 地继续执行进化搜索过程 解决此问题,研究者们逐渐开始考虑引入随机化适 应策略进行参数控制.与将参数设置为固定常数的 2DE算法参数控制与适应策略 经验参数控制不同,这种方法在每代对每个个体根 2.1基于经验的参数控制 据一个预先制定的概率分布模型生成伪随机数作为 在DE算法发展的早期,其参数主要是根据人 参数值,其基本思想与进化算法思想类似,主要是希 为经验设定为一些常数,如文献[1]首先指出F= 望通过生成测试的模式让算法自己选取比较合适 0.5是一个很好的初始选择,如果群体出现早熟收敛 的参数值.常用的概率分布模型有均匀分布(ui- 现象,则应该相应地增大F值,但是小于0.4或大 form distribution)、高斯分布(Gaussian distribution,又 于1的F值往往只在极少数情况下才有用;对于交 称正态分布)、柯西分布(Cauchy distribution)等. 叉概率Pc,该文献则指出0.1是一个合适的初始 文献[8]将每次变异的缩放因子F设置为 选择,但考虑到大的PR值有助于提高算法收敛速 [0.5,1]之间的均匀随机数,提出一种改进的算法 度,PcR=0.8通常也是不错的选择. DERSF;文献[18]修改DE算法的变异模式提出2 文献[11]以实值函数优化问题为背景对DE算 种改进算法DERL和DELB,它们也都使用了均匀 法的参数展开了详细的数值分析,指出了该算法性 随机数生成缩放因子F,均匀随机数的范围限定为 能对参数敏感的问题,这些参数的设定不仅与具体 [-1,-0.4]U[0.4,1].文献[19]提出一种NSDE 问题相关,而且它们之间也相互影响,不易合理设 算法,将DE算法的交叉概率Pc设置为[0,1]之间 置.对缩放因子F,该文献推荐0.6为初始选择,如 的均匀随机数.实验分析发现这些改进算法都优于 果发现算法只能收敛到局部最优,则应适当增大F 参数设置为F=0.5,Pc=0.9的经典DE算法, 值,但当F>1时往往导致群体难以收敛;对于交叉 文献[20]针对多目标优化问题提出一种改进 概率参数,大的PR值有利于增加算法收敛速度,但 的DE算法PDE,该算法中缩放因子F被设置为均 如果过大将有可能导致算法早熟,介于0.3~0.9的 值为0、标准差为1的高斯分布,即F:=N:(0,1),其 值往往是比较好的设置 中表示对每次变异都重新生成一个F值.文献 在与其他算法的性能比较中,文献[12]发现参 [21-22]通过引入多种变异策略提出一种自适应DE 数设置为F=0.5,PcR=0.9的DE算法要显著优于 算法SADE,该算法中缩放因子F被设定为均值为 粒子群优化(particle swarm optimization,PS0)算 0.5、标准差为0.3的高斯分布,即F:=N:(0.5, 法[s1及其改进版本arPS04,也优于简单进化算法 0.3),其中参数0.5是参考了DE算法的经验参数 (simple evolutionary algorithm,SEA)s] 设置,目的是在比较好的经验值附近进行参数随机 也有研究者认为F应该设为稍大值以避免算 化,给生成合适的参数值提供更大可能. 法早熟,如文献[16]中就建议将参数F和Pc都设 由DE变异公式(1)可以看出,缩放因子F与算 置为常数0.9.对于DE算法的经验参数设置,目前 法搜索步长密切相关,在不同的搜索阶段算法可能 研究中一般都认为F=0.5,PcR=0.9是比较有效 偏好不同的搜索步长,比如当群体离全局最优点较 的经典设置7门」 远时,较大的搜索步长将有助于算法快速收敛到好 2.2参数随机化适应策略 的子空间,而当群体离全局最优点较近时,小的搜索 虽然基于经验的参数控制可在一定程度上缓解 步长则有助于算法准确找到更优解a].缩放因子F DE算法的参数控制问题,但是由于这种“经验”通 的经验设置只能提供一种步长选择,而随机化参数 常与具体目标问题密切相关,不同的解空间分布往 设置则可以提供多种选择,这也是随机化参数设置 往具有不同的需求,甚至同一问题的不同进化阶段 通用性更强的原因.但是无论均匀分布还是高斯分

418 智能系统学报 第6卷 布,其搜索步长的广度都是有限的,当算法靠近多极 均值为PcM、标准差较小的高斯分布,算法开始时 值问题的局部最优点时,可能无法提供足够大的步 对每个个体根据式(3)生成一个Pc值 长进行跳跃式搜索,因而仍然存在陷入局部最优的 PCR=N:PCRM,0.1). (3) 风险。 式中:PcM在算法开始时被设置为0.5,在其周围生 针对均匀分布和高斯分布的局限性,研究者们 成的PcR,值将被使用若干代(如SADE算法中设置 开始考虑引入范围更广的柯西分布进行参数随机化 的5代),然后重新按照式(3)生成新的Pc·这样 控制.文献[l9]结合进化规划(evolutionary program- 在每一代演化过程中,能使后代进入下一代的个体, ming,EP)的特点,提出一种邻域控制差分进化算法 对应的PcR,将会被记录在一个数组AR中,经过一定 NSDE,该算法的缩放因子根据式(2)生成。 代数的累积后(如SADE算法中使用的25代),均值 rN(0.5,0.5),ifR(0,1)≤p; F= (2) 将按式(4)更新. lC:(0,1), otherwise. IACR 式中:p设为0.5;N(0.5,0.5)表示均值、标准差均 Pom e(). (4) 为0.5的高斯随机数;C:(0,1)表示位置参数为0、 在每次PcRu更新后,数组AcR将会被清空进入下一 规模参数为1的柯西随机数;R:(0,1)表示(0,1)的 次统计过程 均匀随机数.NSDE算法希望通过式(2)同时兼顾大 文献[24]分析认为当Pc比较小时后代更易于 小搜索步长,从而能有效搜索各种适应度分布特征 进入下一代,但是该后代对应的适应度改进程度通 未知的解空间 常比较小;而大的P值生成的后代虽然相对而言 文献[24]对NSDE算法进行了进一步改进,提 较难进人下一代,但当成功进入下一代时其引起的 出一种SaNSDE算法,其缩放因子F的控制方法与 适应度改进程度往往要大很多,因此式(4)对应的 式(2)类似,只是根据经验将高斯随机数的参数修 适应策略存在将Px取较小值的导向,为缓解此问 正为均值0.5,标准差0.3,并采用适应策略调整式 题,该文献提出一种加权的交叉概率适应策略,其基 (2)中的参数p.SaNSDE算法中参数适应策略的有 本原理与式(4)类似,区别在于每当在数组A中记 效性在很多测试函数上都得到了验证,并成功用于 录成功Pc值的时候,同时在另一数组A△y={△f} 辅助求解问题规模高达1000维的大规模实值优化 中额外记录对应个体的适应度改进值,即△∫= 问题25] f(k)-f(k),然后Pcw的更新公式修正为: 2.3基于统计学习的参数随机化适应策略 IACR (5) 参数随机化适应策略通过将DE算法的参数,即 PcM=∑0AcR(k) 缩放因子F和交叉概率PcR,设置成随机数,增加了 An(k) 0k= (∑AA() (6) 这些参数取值的多样性,从而使算法在面临无任何先 验知识的问题时,仍然能够自动产生适合当前搜索需 实验证明这种改进的参数适应机制使DE算法在一 要的参数值,这在一定程度上提高了算法的性能.然 些复杂测试函数上的性能有了较显著的改进 而,这些用于控制DE算法参数的随机数发生器同样 无论SADE还是SaNSDE都是采用一种离散的方 存在其自身的参数,比如高斯分布的均值和方差,这 式,通过历史信息更新用于参数控制的概率分布,这意 些参数同样需要合理设置.这些参数没有原算法的参 味着只有当历史信息累积一定代数后才能被使用,当 数敏感,在上述参数随机化适应策略中一般都是根据 最大进化代数比较有限时,概率分布的参数被更新的 经验设置,寻求这些参数的最优设置意味着存在进一 频度将会很有限,这将影响参数适应性调整的及时性 步改进DE算法性能的空间,研究者们开始利用统计 文献[9]提出一种改进的DE算法JADE,该方法采用 学习技术分析搜索过程中的历史信息,尝试从中找出 了联系更新的方式适应性调整概率分布的参数.对于 规律以控制随机数发生器的参数, 交叉概率PcR,JADE仍然假设它服从均值为PcRM、标 文献[21-22]通过对交叉概率Pc的分析指出, 准差为0.1的高斯分布,即满足式(3). 该参数在某个小范围内变动时对DE算法性能影响 在每代进化过程中,算法将用SR记录能使对 不大,但该范围不易确定.为解决此问题,该文献提 应后代进入下一代的PcR值,并用式(7)更新PcRw: 出一种SADE算法,它假设交叉概率Pc满足一个 PCRM =(1-c)x PcRM +c x mean(ScR).(7)

第5期 杨振宇,等:差分进化算法参数控制与适应策略综述 419… 式中:参数c是介于(0,1)的实数,JADE中被设置 (12)生成 为c=0.1.对于缩放因子F,该文献假设它服从位置 F:=FA+N(0,1)×(F2+Fa),(11) 参数为Fm,规模参数为0.1的柯西分布: PCR PcRa N(0,1)x (PCRa -PCRe). F:=C:(Fm,0.1). (8) (12) 式中:Fm被初始化为0.5,如果F:不在0~1之间, 式中:N:(0,1)代表均值为0、标准差为1的高斯随 将会被重新生成.在每代进化过程中,能使后代进入 机数;1、2和3表示3个互不相同且也不与i相同 下一代的个体对应的F:值将会被记录在数组S: 的个体下标在这些参数进化完成后,它们将参与到 中,然后根据式(9)更新. DE算法中的包含决策变量的个体的变异和交叉, Fnm=(1-c)×Fm+c×mean(Sp),(9) 由于这些参数值存在于编码中,如果每组参数对应 ∑res,F 生成的后代能成功进入下一代,那么参数本身自然 mean (Sg)= (10) ∑.F 也进入了下一代,从而达到一种控制参数层次的进 式中:mean(·)表示莱默均值(Lehmer mean),这 化与自适应.由于一般要求F和PcR在控制在区间 里使用莱默均值而非一般均值是为了避免出现F [0,1]中,因此如果式(11)、(12)生成的参数值超出 了此范围,将会应用修复规则使它们重新回到此范 过小而导致算法低效的情况. 围.文献[28]在一组多目标问题上测试了SPDE算 文献[26]通过引入基于历史信息的可信度和 影响适应度值变化程度的加权机制,将上述2种适 法的性能,与其他13种算法的比较表明了这种自适 应策略扩展为控制任意与个体相关联的算法参数的 应策略比较有效.类似地,文献[29]建议用如下这 一般性方法,其基本思想是首先假设该参数的分布 种方式自适应控制参数F: 满足某个概率模型,然后通过统计学习的方法逐渐 F:=FH+N:(0,0.5)×(F2-Fa).(13) 调整概率模型的参数.该文献使用这种一般性的参 而交叉概率Pcπ被设置为根据均值为0.5、标准差为 数随机化适应方法提出一种改进的DE算法GaDE, 0.15的高斯随机数N(0.5,0.15)生成.文献[30]指 并将其成功用于求解大规模实值优化问题. 出,根据这种自适应策略设计的SDE算法要优于文 大量的实验结果表明,基于统计学习的参数随 献[28]中的SPDE算法. 机化适应策略不仅优于经验参数设置,而且由于这 文献[10]提出一种改进的DE算法DE,它采 类方法可以从历史信息中学习出一些参数变化趋 用了另一种参数自适应策略.算法DE同样将F,和 势,比简单的参数随机化适应策略更有方向性,当这 PcR,与每个个体关联起来放入个体编码,算法开始 种方向性比较准确时,这类方法将更有效, 时F:和PcR被分别初始化0.5和0.9,然后每代在 2.4参数自适应策略 决策变量进化前按式(14)、(15)更新, 根据文献[27]的定义,参数适应与自适应策略 「F+R1×F.,ifR2≤T1; F,= (14) 的本质区别在于后者须将算法参数放入个体编码中 otherwise. 与决策变量一同进化.依据这个条件,无论是参数随 「R3,ifR4≤T2; PCR: (15) 机化策略还是基于统计学习的参数随机化策略都只 IPcR:,otherwise. 能称之为适应策略,而自适应策略一般被认为是进 式中:R(0∈{1,2,3,4})是[0,1]的均匀随机数;T1 化算法参数控制的最高级手段,在DE算法领域同 和T2分别表示更新参数F和Pc的概率,在DE中 样存在相关工作. 被设置为r1=r2=0.1;为了使新的F:在[0.1,1.0] 既然DE是一种非常有效的参数优化算法,那 之间,F,和F分别被设置为0.1和1.0.文献[10] 么一种非常直观的自适应策略就是仍然采用DE这 中设计了大量的数值实验分析了这种自适应策略的 种模式来进化其自身的参数F和Pc·文献[28]提 效果,实验结果表明这种自适应策略在求解实值函 出一种SPDE算法,该算法首先对每个个体都增加 数优化问题时非常有效,使DE成为目前最为高效 F:和Pc这2个参数作为决策变量放入个体表示, 的DE改进算法之一 在算法开始时F:和Pc,被初始化为[0,1]的均匀随 表1简要列出了本节介绍的各种DE算法变种 机数,然后在每代进化运算时,首先根据式(11)、 及其采用的参数控制与适应策略

·420 智能系统学报 第6卷 表1DE算法变种及其对应的参数控制与适应策略 Table 1 DE variants and the corresponding parameter control and adaptation strategies 类别 算法 Pc 文款出处 DE 常数0.5 常数0.1或0.9 [1] DE 区间[0.6,1]内常数 区间[0.3,0.9]内常数 [11] 经验参数控制 DE 常数0.5 常数0.9 [12] DE 常数0.9 常数0.9 [16] ODE 常数0.5 常数0.9 [17] DERSF 均匀随机数R(0.5,1) 常数0.9 [8] SADE 高斯随机数N(0.5,0.3) 式(3)、(4) [21] 参数随机化适应 NSDE 式(2) 均匀随机数R(0,1)》 [19] SaNSDE 式(2) 式(3)、(5)、(6) [24] JADE 式(8)~(10)》 式(3)、(7) [9] SPDE 式(11) 式(12) [28] 参数自适应 SDE 式(13) 高斯随机数N(0.5,0.15) [29] jDE 式(14) 式(15) [10] 3实验分析 在测试集方面,采用了13个被广泛使用的经典 实值函数优化函数[2],表3给出了这些函数的定义 本文前面系统介绍了目前DE算法研究领域常 与搜索空间.其中函数~ff和f是单峰函数 用的参数控制与适应策略,为了对这些策略的实际 (即只有1个极值点),函数f~f3是多峰函数, 效果有更直观的认识,笔者以实值函数优化为问题 而且极值点的个数非常多],所有测试函数都被设 背景设计了一组实验进行验证.为保证实验结果比 定为30维,其最优值皆为0. 较的公平性,所有算法都采用经典DE变异公式(即 在参数设置方面,所有算法的群体大小都设为 式(1)),用表2来标记要测试的算法及其对应的参 100,其参数F与P的设置则按照表2及相关文献 数控制策略 中的描述,对于比较复杂的函数f4∫5√f和f进 表2测试的DE算法变种及其参数控制与适应策略 化代数V设定为5000,而对于相对简单的其他函 Table 2 The tested DE variants and their parameter con- 数,进化代数N设定为1500.对于每个测试函数,每 trol and adaptation strategies 个算法都独立运行30次统计实验结果,并计算均值 算法标识 F PCR 与方差,表4和表5分别列出了算法在单峰和多峰 DE 常数0.5 常数0.9 函数上的均值与方差 DEU 随机数R(0,1) 随机数R(0,1) 从表4的结果可以看出,基于经验参数设置的 DEG 随机数N(0.5,0.3)随机数N(0.9,0.1) 随机数C(0.5,0.1)随机数C(0.9,0.1) 经典DE算法在函数ff方和f6上具有不错的结果, DEC SADE' 按SADE方式自适应按SADE方式自适应 但在其他函数上结果稍差,采用参数随机化适应策 JADE 按JADE方式自适应按JADE方式自适应 略的算法DE"、DES和DEC一般比经典DE算法结 jDE 按DE方式自适应按jDE方式自适应 果更好,而在函数∫4上结果却变得更差,说明参数 由表2可以看出,第1种方法是采用经验参数 随机化并不总是有效,这3个算法中使用高斯随机 设置的经典DE算法:接下来是3种采用参数随机 数的DE“效果最好.对于基于统计学习的参数随机 化适应策略的算法,分别对应均匀分布、高斯分布和 化适应策略SADE*和JADE,它们在这些单峰函数 柯西分布;第5、6种算法采用基于统计学习的参数 上结果并不突出,仅在比较复杂的f上取得了更好 随机化适应策略,分别按文献[21]中的SADE和文 结果.采用参数自适应的算法DE几乎在所有函数 献[9]中的JADE所采用的策略进行参数控制,由于 上都取得了更好的结果,说明这种参数自适应策略 这2种算法还采用了其他策略进一步改进算法性 对求解单峰函数比较有效. 能,与这里只采用经典变异公式的方法稍有区别,分 从表5中算法在多峰函数上的结果看,经典DE 别用SADE·和JADE来标记它们以示区别;最后一 算法在比较复杂的函数f和f)上结果很差,在其他 种采用参数自适应策略,与文献[10]中的DE完全 函数上结果一般.使用均匀随机数的DE"算法在大 致 部分问题上都得到了更好结果,但在函数∫上的结

第5期 杨振宇,等:差分进化算法参数控制与适应策略综述 421 果变得很差;使用高斯随机数的DE算法只在函数 函数上都取得了更好结果,而另一种JADE·则在函 f~fio上得到了更好结果;使用柯西随机数的DE 数f和f)上性能有显著提高.对于自适应参数控制 算法在函数方和f上结果不理想.采用基于统计学 算法DE,它在除天外的函数上都取得了明显更好 习参数随机化适应策略的算法SADE·在除f外的 的结果 表3经典实值优化测试函数集 Table 3 Classical benchmark functions for real-valued optimization 测试函数 搜索空间 回-新 [-100,100] ()=2x1+ [-10,10] 6)-8(含护 [-100,100] f4(x)=malx:l,1≤i≤30y [-100,100] )=80(-产+g-时 [-30,30] f6(x)=(Lx:+0.5J)2 [-100,100] 方(倒=2试+nmd[0,1) [-1.28,1.28] (e)=-含((国可)+30x41g9g2g72n438 [-500,500] 6()=2[号-10cs(2a)+10] [-5.12,5.12] -(-02√2深-(m2小+20+e [-32,32] f(倒-m)1 [-600,600] 国-号0m(r)+8i6-11+0(o]+.-0+宫0.10利 [-50,50] 力=01m(3a)+8-i01+m2(3n】+-[1+m(2+2(5.10,4 [-50,50] 表4采用各种不同参数控制与适应策略的DE算法在单峰函数上的结果 Table 4 Results of DE with different parameter control and adaptation strategies for unimodal functions 算法 h 6 fa 参数 6 N=1500 N=1500 W=5000 N=5000 N=1500 N=1500 均值 1.83e-13 1.19e-06 7.86e-11 2.91e-02 0.00e+00 9.67e-03 DE 方差 1.26e-13 7.19e-07 6.06e-11 7.33e-02 0.00e+00 2.78e-03 均值 3.13e-22 9.72e-14 3.99e-05 6.96e-02 0.00e+00 9.45e-03 DE 方差 2.14e-22 2.46e-14 7.00e-05 3.21e-01 0.00e+00 1.80e-03 均值 5.02e-24 3.61e-13 4.10e-15 7.37e+00 0.00e+00 5.92e-03 DEG 方差 3.50e-24 2.25e-13 6.61e-15 2.97e+00 0.00e+00 1.53e-03 均值 3.03e-20 7.18e-11 1.07e-13 5.36e+00 0.00e+00 7.33e-03 DES 方差 2.91e-20 4.49e-11 1.25e-13 2.41e+00 0.00e+00 2.25e-03 均值 7.34e-21 4.34e-13 3.55e+02 2.28e-05 0.00e+00 9.68e-03 SADE' 方差 3.83e-21 9.67e-14 5.11e+02 1.23e-04 0.00e+00 1.91e-03 均值 4.09e-10 7.71e-06 5.65e+03 1.26e-02 0.00e+00 1.03e-02 JADE· 方差 6.07e-10 5.48e-06 2.49e+03 4.68e-02 0.00e+00 2.84e-03 均值 3.00e-28 5.13e-17 5.93e-14 2.19e-15 0.00e+00 7.03e-03 jDE 方差 2.32e-28 2.85e-17 1.02e-13 1.45e-15 0.00e+00 2.00e-03
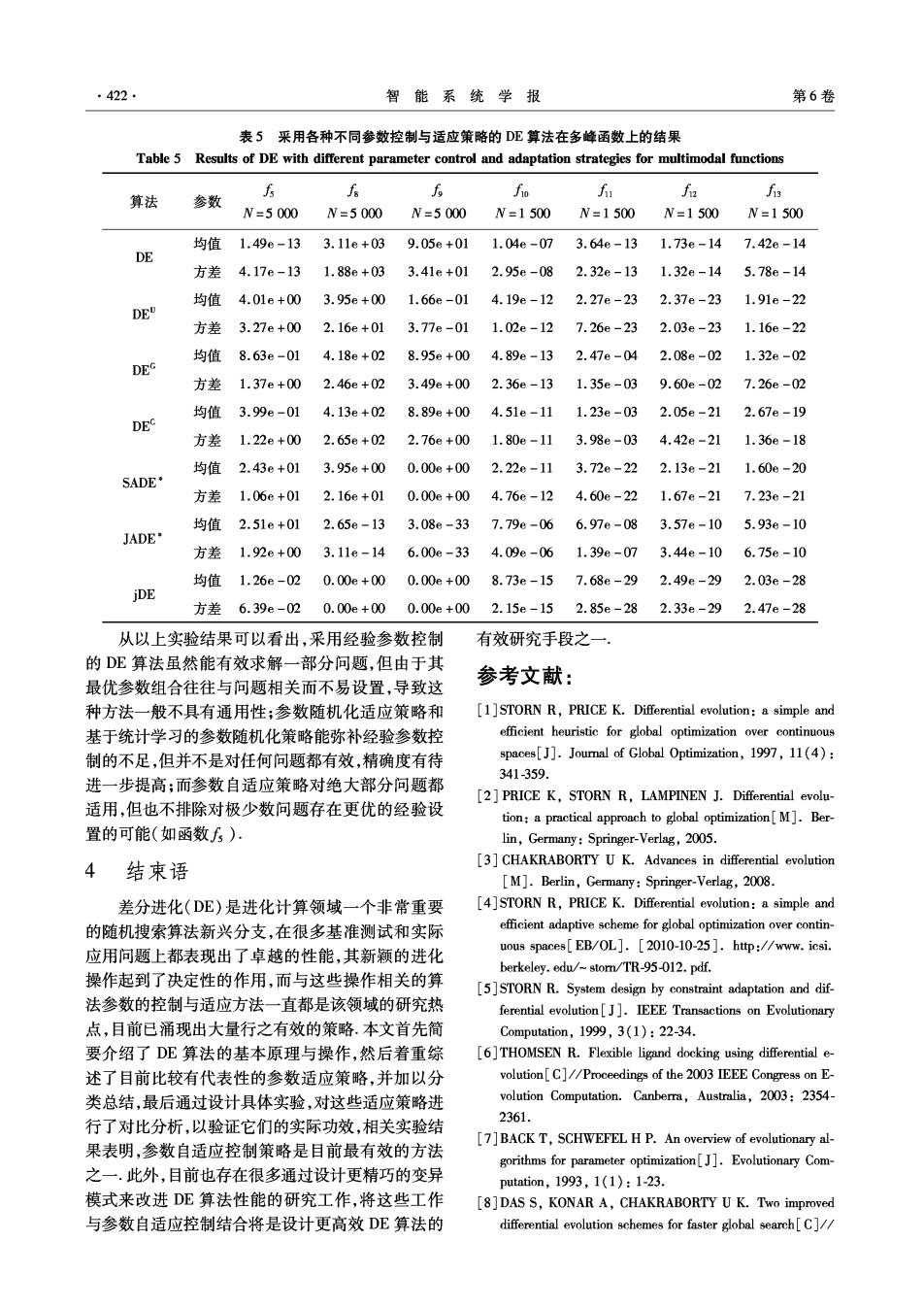
·422 智能系统学报 第6卷 表5采用各种不同参数控制与适应策略的DE算法在多峰函数上的结果 Table 5 Results of DE with different parameter control and adaptation strategies for multimodal functions 算法 6 参数 公 f和 N=5000 W=5000N=5000N=1500N=1500N=1500 N=1500 均值 1.496-13 3.11e+03 9.056+01 1.04e-073.64e-131.73e-14 7.426-14 DE 方差 4.17e-13 1.88e+03 3.41e+012.95e-08 2.32e-131.32e-14 5.78e-14 均值4.01e+00 3.95e+001.66e-014.19e-122.27e-232.37e-231.91e-22 DEU 方差3.27e+00 2.16e+013.77e-011.02e-127.26e-23 2.03e-23 1.16e-22 均值8.63e-014.18e+028.95e+004.89e-132.47e-042.08e-02 1.32e-02 DEG 方差 1.37e+002.46e+023.49e+002.36e -13 1.35e-039.60e-02 7.26e-02 均值3.99e-01 4.13e+02 8.89e+00 4.51e 1.23e-03 2.05e-21 2.67e-19 DEC 方差 1.22e+00 2.65e+02 2.76e+00 1.80e 3.98e-03 4.42e-21 1.36e-18 均值2.43e+01 3.95e+00 0.00e+00 2.22e 3.72e-22 2.13e-21 1.60e-20 SADE· 方差1.06e+012.16e+01 0.00e+00 4.76e-12 4.60e-221.67e-21 7.236-21 均值 2.51e+01 2.65e-13 3.086-337.79e-066.97e-083.57e-10 5.93e-10 JADE* 方差1.92e+003.11e-146.00e-334.09e-061.39e-073.44e-10 6.756-10 均值1.26e-020.00e+000.00e+008.73e-157.68e-292.49e-292.03e-28 jDE 方差6.39e-020.00e+000.00e+00 2.15e-15 2.85e-282.33e-29 2.47e-28 从以上实验结果可以看出,采用经验参数控制 有效研究手段之一. 的DE算法虽然能有效求解一部分问题,但由于其 最优参数组合往往与问题相关而不易设置,导致这 参考文献: 种方法一般不具有通用性参数随机化适应策略和 [1]STORN R,PRICE K.Differential evolution:a simple and 基于统计学习的参数随机化策略能弥补经验参数控 efficient heuristic for global optimization over continuous 制的不足,但并不是对任何问题都有效,精确度有待 spaces[J].Joural of Global Optimization,1997,11(4): 341-359. 进一步提高;而参数自适应策略对绝大部分问题都 [2]PRICE K,STORN R,LAMPINEN J.Differential evolu- 适用,但也不排除对极少数问题存在更优的经验设 tion:a practical approach to global optimization[M].Ber- 置的可能(如函数∫5). lin,Germany:Springer-Verlag,2005. 4结束语 [3]CHAKRABORTY U K.Advances in differential evolution [M].Berlin,Germany:Springer-Verlag,2008. 差分进化(DE)是进化计算领域一个非常重要 [4]STORN R,PRICE K.Differential evolution:a simple and 的随机搜索算法新兴分支,在很多基准测试和实际 efficient adaptive scheme for global optimization over contin- 应用问题上都表现出了卓越的性能,其新颖的进化 uous spaces[EB/OL].[2010-10-25 ]http://www.icsi. berkeley.edu/-stom/TR-95-012.pdf. 操作起到了决定性的作用,而与这些操作相关的算 [5]STORN R.System design by constraint adaptation and dif- 法参数的控制与适应方法一直都是该领域的研究热 ferential evolution[J].IEEE Transactions on Evolutionary 点,目前已涌现出大量行之有效的策略.本文首先简 Computation,1999,3(1):22-34. 要介绍了DE算法的基本原理与操作,然后着重综 [6]THOMSEN R.Flexible ligand docking using differential e- 述了目前比较有代表性的参数适应策略,并加以分 volution[C]//Proceedings of the 2003 IEEE Congress on E- 类总结,最后通过设计具体实验,对这些适应策略进 volution Computation.Canberra,Australia,2003:2354- 行了对比分析,以验证它们的实际功效,相关实验结 2361. [7]BACK T,SCHWEFEL H P.An overview of evolutionary al- 果表明,参数自适应控制策略是目前最有效的方法 gorithms for parameter optimization[J].Evolutionary Com- 之一.此外,目前也存在很多通过设计更精巧的变异 putation,1993,1(1):1-23. 模式来改进DE算法性能的研究工作,将这些工作 [8]DAS S,KONAR A,CHAKRABORTY U K.Two improved 与参数自适应控制结合将是设计更高效DE算法的 differential evolution schemes for faster global search[C]//

第5期 杨振宇,等:差分进化算法参数控制与适应策略综述 ·423· Proceedings of the 2005 Genetic and Evolutionary Computa- volution algorithm for numerical optimization[C]//Pro- tion Conference.Washington,DC.USA.2005:991-998. ceedings of the 2005 IEEE Congress on Evolution Compu- [9]ZHANG J,SANDERSON A C.JADE:adaptive differential tation.Edinburgh,UK,2005:1785-1791. evolution with optimal external archive[J].IEEE Transac- [22]QIN A K,HUANG V L,SUGANTHAN P N.Differential tions on Evolutionary Computation,2009,13(5):945- evolution algorithm with strategy adaptation for global nu- 958. merical optimization[J].IEEE Transactions on Evolution- [10]BREST J,GREINER S,BOSKOVC B,et al.Self-adap- ary Computation,2009,13(2):398-417. ting control parameters in differential evolution:a compara- [23]YAO Xin,LIU Yong,LIN Guangming.Evolutionary pro- tive study on numerical benchmark problems[J].IEEE gramming made faster[J].IEEE Transactions on Evolu- Transactions on Evolutionary Computation,2006,10(6): tionary Computation,1999,3(2):82-102. 646-657. [24]YANG Zhenyu,TANG Ke,YAO Xin.Self-adaptive differ- [11]GAMPERLE R,MULLER S,KOUMOUTSAKOS P.A pa- ential evolution with neighborhood search[C]//Proceed- rameter study for differential evolution[C]//WSEAS Inter- ings of the 2008 IEEE Congress on Evolution Computation. national Conference on Advances in Intelligent Systems, Hong Kong,China,2008:1110-1116. Fuzzy Systems,Evolutionary Computation.Interlaken, [25]YANG Zhenyu,TANG Ke,YAO Xin.Large scale evolu- Switzerland,2002:293-298. tionary optimization using cooperative coevolution[J].In- [12]VESTERSTROM J,THOMSEN R.A comparative study of formation Sciences,2008,178(15):2985-2999. differential evolution,particle swarm optimization and evo- [26]YANG Zhenyu,TANG Ke,YAO Xin.Scalability of gen- lutionary algorithms on numerical benchmark problems eralized adaptive differential evolution for large-scale con- [C]//Proceedings of the 2004 IEEE Congress on Evolu- tinuous optimization [J].Soft Computing,2011 (in tion Computation.Portland,USA,2004:1980-1987. press). [13]KENNEDY J,EBERHART R C.Particle swarm optimiza- [27]HINTERDING R,MICHALEWICZ Z,EIBEN A E.Adap- tion[C]//IEEE International Conference on Neural Net- tation in evolutionary computation:a survey [C]//Pro- works.Perth,Australia,1995:1942-1948. ceedings of the 1997 IEEE International Conference on Ev- [14]RIGET J,VESTERSTROM J.A diversity-guided particle olutionary Computation.Indianapolis,USA,1997:65-69. swarm optimizer-the arPSO,Technical Report 2002-02 [28]ABBASS H A.The self-adaptive Pareto differential evolu- [R].Aarhus,Denmark:Department of Computer Sci- tion algorithm [C]//Proceedings of the 2002 IEEE Con- ence,University of Aarhus,2002. gress on Evolution Computation.Honolulu,USA,2002: [15]THOMSEN R.Flexible ligand docking using evolutionary 831-836. algorithms:investigating the effects of variation operators [29]OMRAN M,SALMAN A,ENGELBRECHT A.Self-adap- and local search hybrids[J].BioSystems,2003,72 (1/ tive differential evolution[C]//Proceedings of the Interna- 2):57-73. tional Conference on Computational Intelligence and Secur- [16]ROMKKONEN J,KUKKONEN S,PRICE K V.Real-pa- ity.Xi'an,China,2005:192-199. rameter optimization with differential evolution[C]//Pro- [30]SALMAN A,ENGELBRECHT A,OMRAN M.Empirical ceedings of the 2005 IEEE Congress on Evolution Computa- analysis of self-adaptive differential evolution[J].Europe- tion.Edinburgh,UK,2005:506-513. an Joural of Operational Research,2007,183(2):785- [17]RAHNAMAYAN S,TIZHOOSH H R,SALAMA M A. 804. Opposition-based differential evolution[J].IEEE Transac- 作者简介: tions on Evolutionary Computation,2008,12(1):64-79. 杨振宇,男,1982年生,讲师,博士, [18]KAELO P,ALI MM.A numerical study of some modified 主要研究方向为进化计算与应用,发表 differential evolution algorithms[J].European Journal of 学术论文多篇,其中被SCI、EI检索10 0 perational Research,2006,169(3):1176-1184. 余篇. [19]YANG Zhenyu,YAO Xin,HE Jingsong.Making a differ- ence to differential evolution M ]//MICHALEWICZ Z, SIARRY P.Advances in Metaheuristics for Hard Optimiza- tion.Berlin,Germany:Springer,2008:397-414. 唐珂,男,1981年生,教授,博士, 20]ABBASS H A,SARKER R,NEWTON C.PDE:a Pareto- IEEE Computational Intelligence Magazine frontier differential evolution approach for multi-objective 副编辑,EEE计算智能协会Emergent optimization problems[C]//Proceedings of the 2003 IEEE Technologies Technical Committee委员. Congress on Evolution Computation.Canberra,Australia, 主要研究方向为计算智能、机器学习、 2003:971-978 模式识别等,发表学术论文50余篇。 [21]QIN A K,SUGANTHAN P N.Self-adaptive differential e-