第3章电阻电路的一磐分析例1图示为电路的图,画出兰种奇能的树及真对应的基本回路88E.注意网孔为基本回路
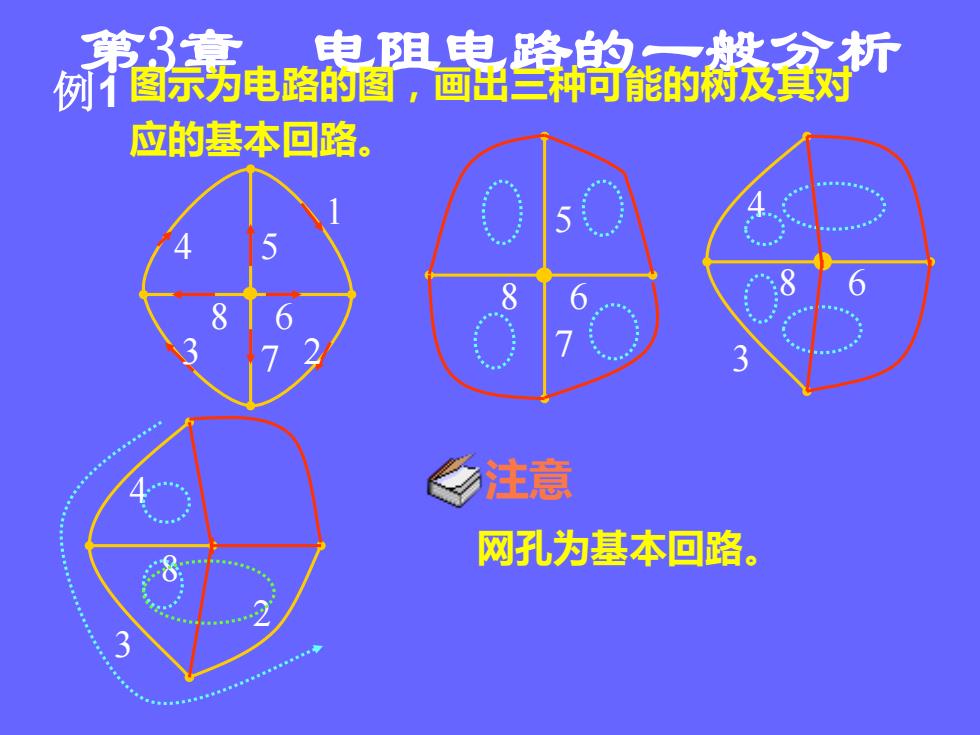
第3章 电阻电路的一般分析 例1 8 7 6 4 5 3 2 1 图示为电路的图,画出三种可能的树及其对 应的基本回路。 8 7 6 5 8 6 4 3 8 2 4 3 注意 网孔为基本回路
·例2有6个支路电流,需列写6个方程。KCL方程:R4R2i+i-i=013122①R3?-i +i +i=0-i-i+i=0R15Rs取网孔为独立回路,沿顺时3④福6针方向绕行列KVL写方程:十R6us+-=0回路1-s- = 0回路2u, +s+u=0回路3
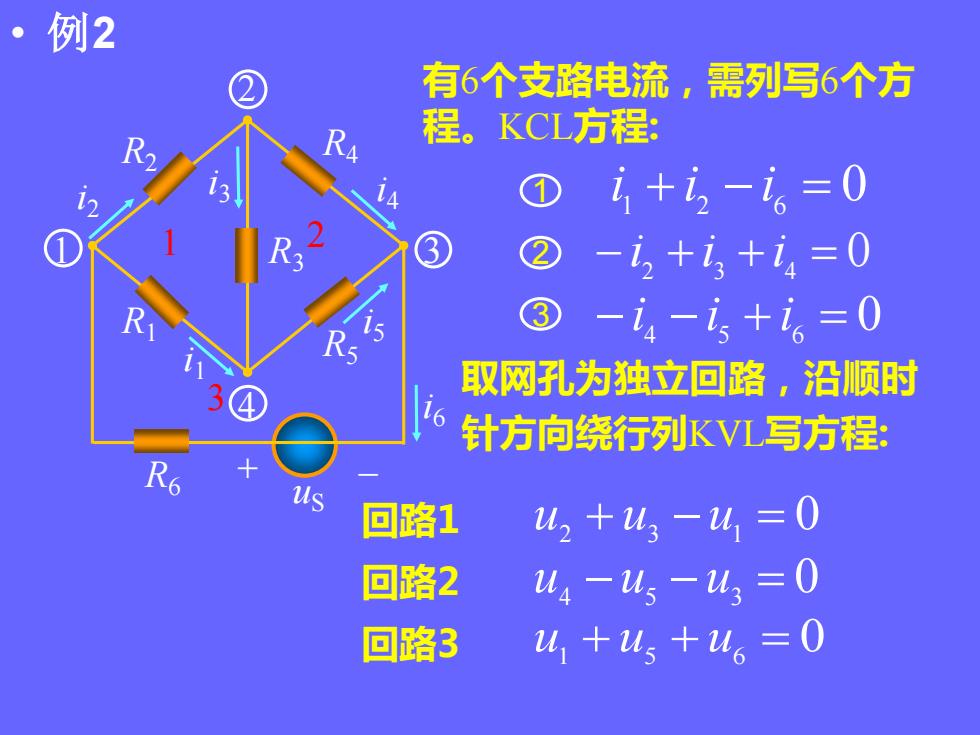
• 例2 0 1 i 1 + i 2 − i 6 = 3 2 0 − i 4 − i 5 + i 6 = 0 − i 2 + i 3 + i 4 = 有6个支路电流,需列写6个方 程。KCL方程: 取网孔为独立回路,沿顺时 针方向绕行列KVL写方程: u2 + u3 − u1 = 0 0 u4 − u5 − u3 = u1 + u5 + u6 = 0 回路1 回路2 回路3 1 2 3 R1 R2 R3 R4 R5 R6 + – i2 i3 i4 i1 i5 i6 uS 1 2 3 4
这一步可+-= 0回路1以省去-,=0回路2 +s +,=0回路3应用欧姆定律消去支路电压得:R4R213Ri +Ri-Ri=0①R323Ri - Ris - Ri, = OR115RsRi +Ris + Ri =us④R6us
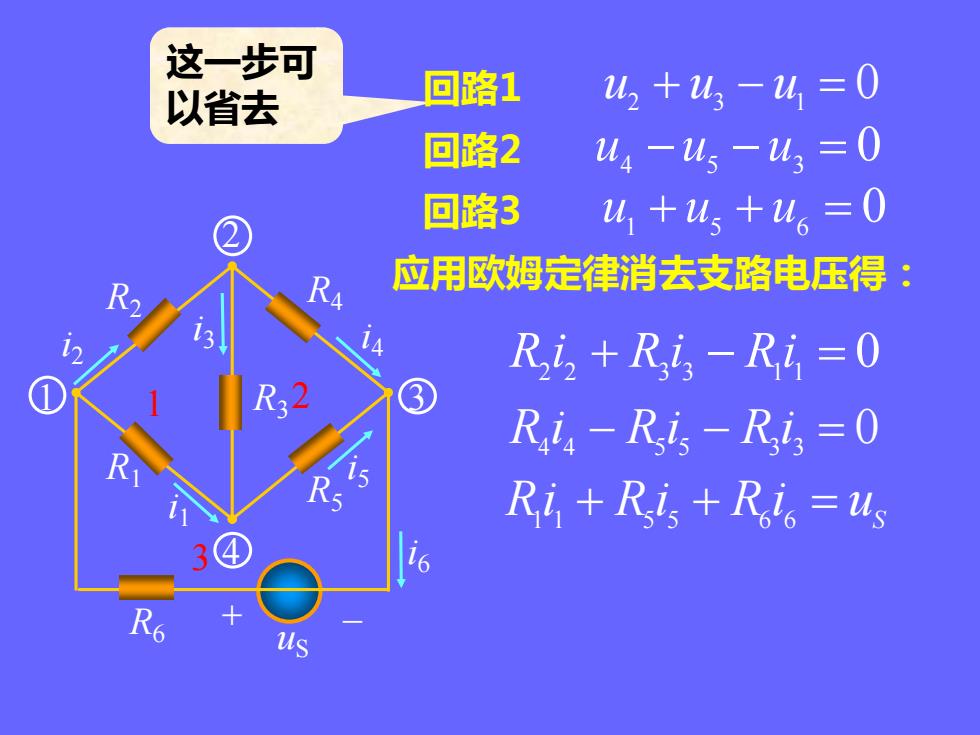
应用欧姆定律消去支路电压得: 0 R2 i 2 + R3 i 3 − R1 i 1 = 0 R4 i 4 − R5 i 5 − R3 i 3 = S Ri + R i + R i = u 1 1 5 5 6 6 这一步可 以省去 0 u2 + u3 − u1 = 0 u4 − u5 − u3 = 0 u1 + u5 + u6 = 回路1 回路2 回路3 R1 R2 R3 R4 R5 R6 + – i2 i3 i4 i1 i5 i6 uS 1 2 3 4 1 2 3
例3求各支路电流及各电压源发出的功率a解①n-1=1个KCL方程:131127Q12结点a:-1i-12+13=070270V6V②b-(n-1)=2个KVL方程:71,-111,=70-6=646111,+71=62ZU-ZUs
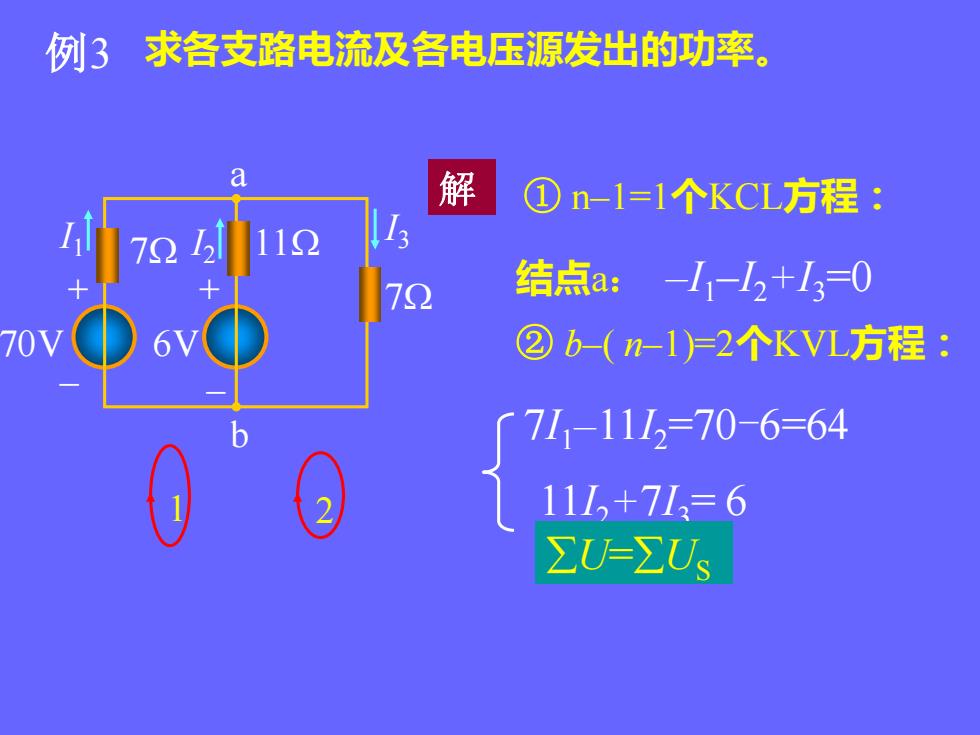
例3 求各支路电流及各电压源发出的功率。 1 2 解 ① n–1=1个KCL方程: 结点a: –I1–I2+I3=0 ② b–( n–1)=2个KVL方程: 11I2+7I3 = 6 7I1–11I2=70-6=64 U=US 70V 6V 7 b a + – + – I1 I3 I 7 2 11
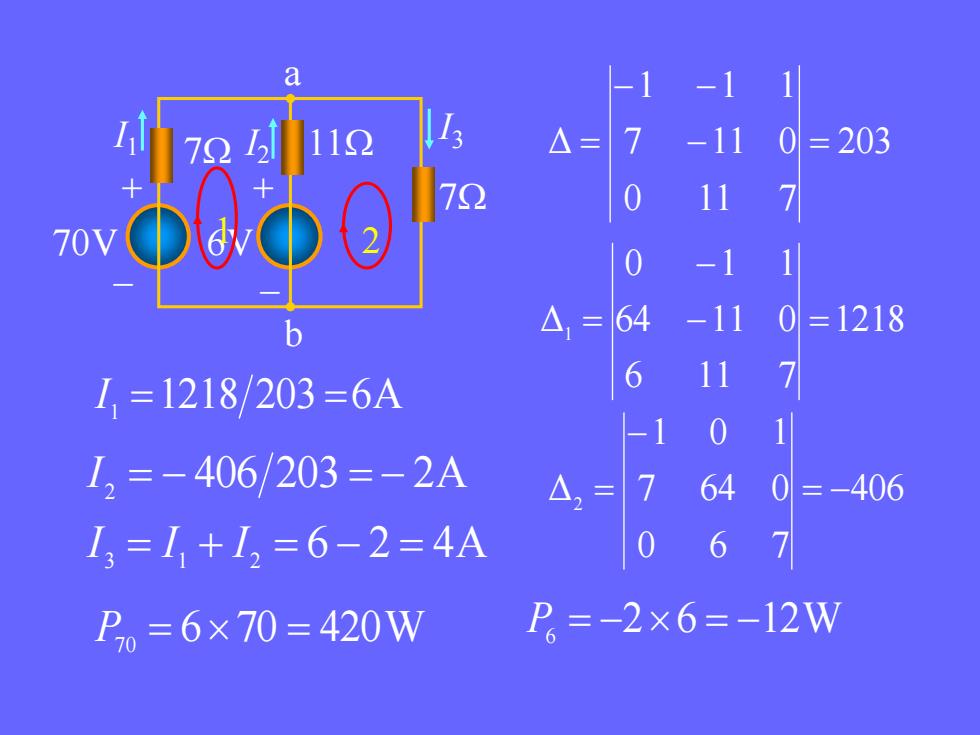
a113A-110=203112A=7272+X72711O70V10-11O=1218△, =64b1176I, =1218/203=6A0I, = - 406/203 = - 2A64=-406△.=1I, =I+I,=6-2=4A06P, =-2x6=-12WPo = 6 × 70 = 420W
203 0 11 7 7 11 0 1 1 1 Δ − = − − = 1218 6 11 7 64 11 0 0 1 1 Δ1 − = − = 406 0 6 7 7 64 0 1 0 1 Δ2 = − − = I 1 =1218 203 =6A I 2 = − 406 203 = − 2A I 3 = I 1 + I 2 = 6 − 2 = 4A P70 = 670 = 420W P6 = −26 = −12W 70V 6V 7 b a + – + – I1 I3 I 7 2 11 2 1
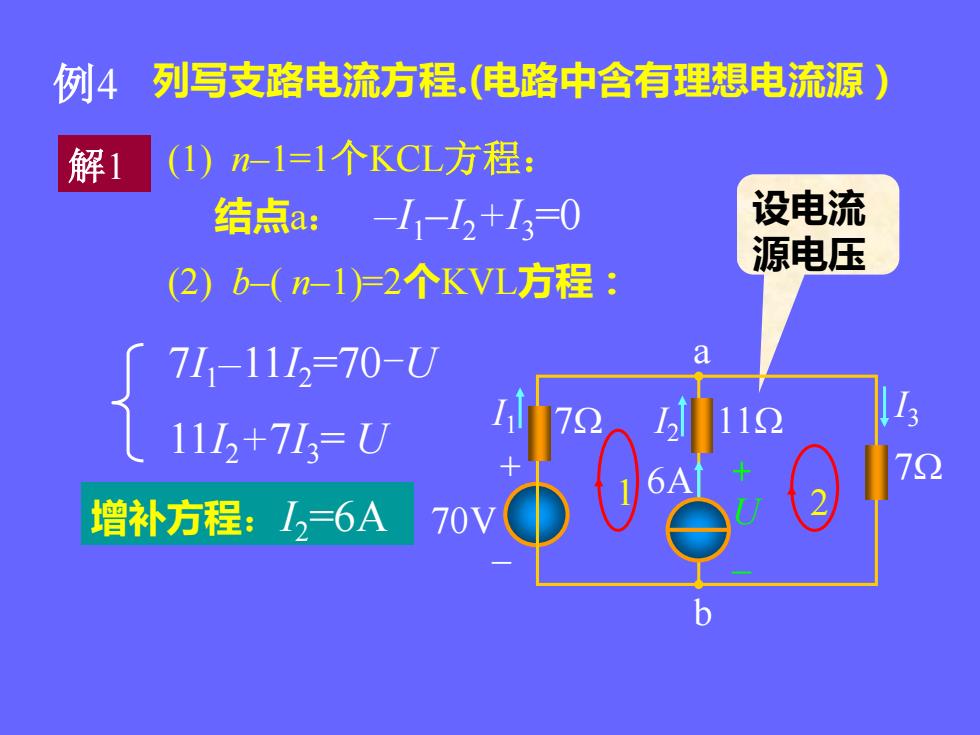
例4列写支路电流方程.(电路中含有理想电流源)(1)n-1=1个KCL方程:解1设电流结点a:-l-12+13=0源电压(2) b-(n-1)=2个KVL方程:a71,-1112=70-U5112721111+71=U726A增补方程:I=6A70V福
例4 结点a: –I1–I2+I3=0 (1) n–1=1个KCL方程: 列写支路电流方程.(电路中含有理想电流源) 解1 (2) b–( n–1)=2个KVL方程: 11I2+7I3 = U 7I1–11I2=70-U 增补方程:I2=6A 设电流 源电压 + U _ a 70V 7 b + – I1 I3 I 7 2 11 2 1 6A
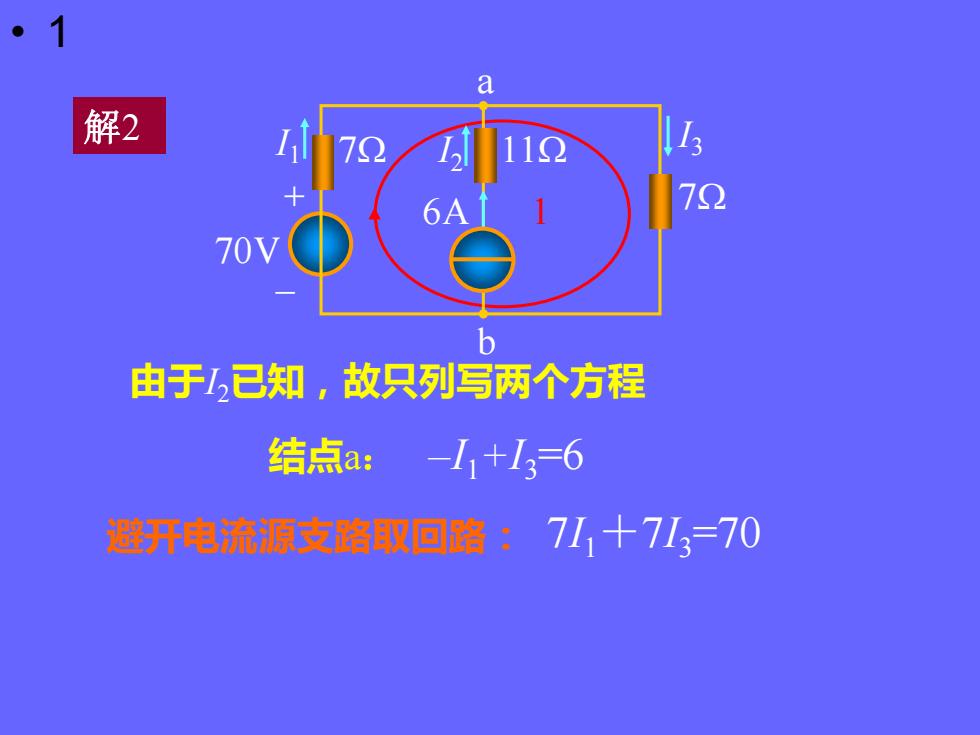
·1a解21127212726A70Vb由于,已知,故只列写两个方程结点a:-1i+13=6避开电流源支路取回路:71,十713=70
• 1 1 解2 由于I2已知,故只列写两个方程 结点a: –I1+I3=6 避开电流源支路取回路: 7I1+7I3=70 70V 7 b a + – I1 I3 I 7 2 11 6A

例5列写支路电流方程.(电路中含有受控源a结点a:解1317212112十-l1-12+13=072十71,-111,=70-5U70V5U111+71=5Ub增补方程:U=7L注意有受控源的电路,方程列写分两步:①先将受控源看作独立源列方程②将控制量用未知量表示,并代入①中所列的方程,消去中间变量
例5 –I1–I2+I3=0 列写支路电流方程.(电路中含有受控源) 解 11I2+7I3 = 5U 7I1–11I2=70-5U 增补方程:U=7I3 有受控源的电路,方程列写分两步: ①先将受控源看作独立源列方程; ②将控制量用未知量表示,并代入①中所列的方程, 消去中间变量。 注意 5U + U 70V _ 7 b a + – I1 I3 I 7 2 11 2 1 + _ 结点a:

例6用网孔电流法求解电流选网孔为独立回路:解(Rs+R+R)i-Ri-Ri=URi+(R+R+Ri-Ri=0-Ri-Ri +(R +R+R)i =0i=iz-is表明3RR2①无受控源的线性网络Rk=RkjRs系数矩阵为对称阵②当网孔电流均取顺(或逆)UR13R3时针方向时,R均为负
例6 用网孔电流法求解电流 i 解 选网孔为独立回路: i1 i3 i2 S US (R + R1 + R4 )i 1 − R1 i 2 − R4 i 3 = − R1 i 1 + (R1 + R2 + R5 )i 2 − R5 i 3 = 0 − R4 i 1 − R5 i 2 + (R3 + R4 + R5 )i 3 = 0 ①无受控源的线性网络Rjk=Rkj , 系数矩阵为对称阵。 ②当网孔电流均取顺(或逆) 时针方向时,Rjk均为负。 2 3 i = i − i RS R5 R4 R3 R1 R2 US + _ i 表明

例7增补方程:RR212Rs-U=Ri(R+R+R)i-Ri-Ri=U受控源看-Ri+(R+R)i =5U作独立源-Ri+(R +R)i =-5U列方程
例7 i1 i3 i2 S US (R + R1 + R4 )i 1 − R1 i 2 − R4 i 3 = − R1 i 1 + (R1 + R2 )i 2 = 5U − R4 i 1 + (R3 + R4 )i 3 = −5U 受控源看 作独立源 列方程 3 3 U = R i 增补方程: RS 5U R4 R3 R1 R2 US + _ _ + + _ U