
Chapter 2Basic lawsSJTU
SJTU 1 Chapter 2 Basic laws
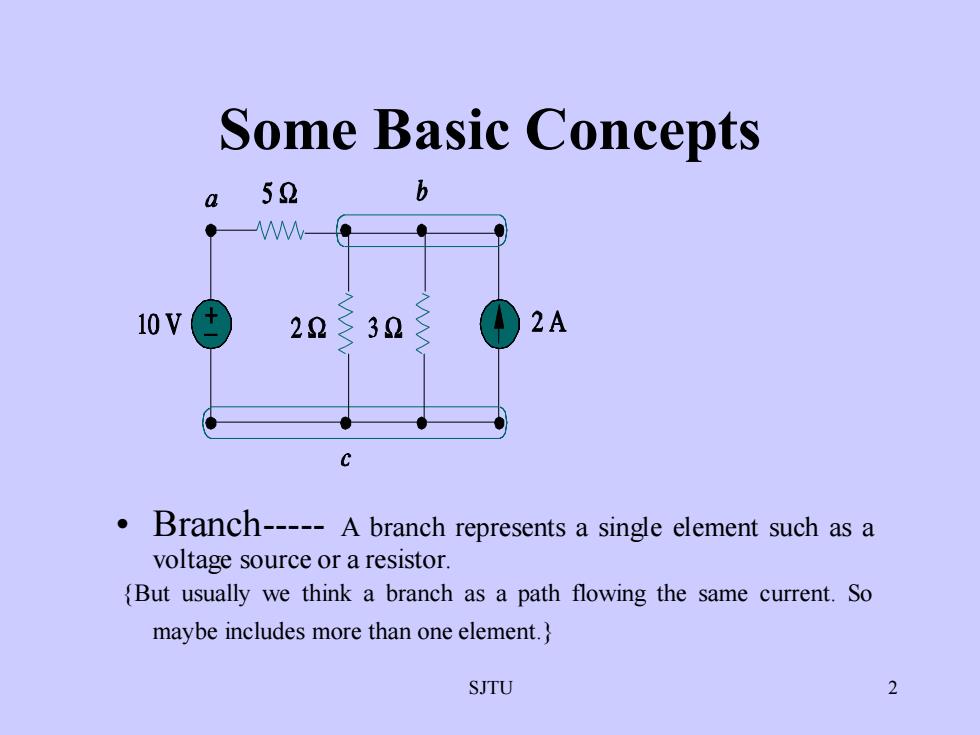
SomeBasic Conceptsb52a2A10V2232. Branch----- A branch represents a single element such as avoltage source or a resistor.(But usually we think a branch as a path flowing the same current. Somaybe includes more than oneelement.2SJTU
SJTU 2 Some Basic Concepts • Branch- A branch represents a single element such as a voltage source or a resistor. {But usually we think a branch as a path flowing the same current. So maybe includes more than one element.}
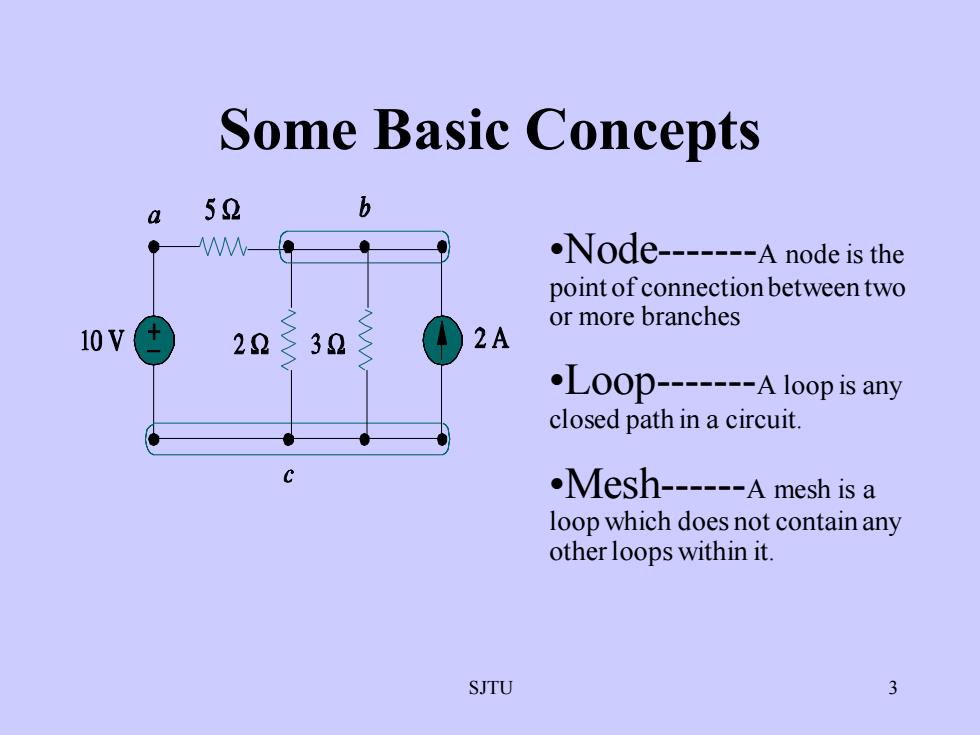
Some Basic Conceptsb52a.Node-------A node is thepointof connection between twoormorebranches2A10 V2232·Loop0--.----Aloopis anyclosed path in a circuit.·Mesh------A mesh is aloop which does not contain anyotherloops within it3SJTU
SJTU 3 •Node-A node is the point of connection between two or more branches •Loop-A loop is any closed path in a circuit. •Mesh-A mesh is a loop which does not contain any other loops within it. Some Basic Concepts

KIRCHHOFF'S LAWS Kirchhoff'sCurrentLaw(KCL):NZi=0k-1isWThe algebraic sum of currents entering anode(oraclosedboundary)iszero.(Based on the law of conservation ofi3charge)The sum of the currents entering a node =the sum ofthe currentsleaving the node-iz+i +i-is =0or i+is+i=iz+isSJTU
SJTU 4 KIRCHHOFF’S LAWS • Kirchhoff’s Current Law (KCL): The algebraic sum of currents entering a node (or a closed boundary)is zero. (Based on the law of conservation of charge) The sum of the currents entering a node = the sum of the currentsleaving the node. = = N k k i 1 0 1 3 4 2 5 1 2 3 4 5 0 or i i i i i i i i i i + + = + − + + − =
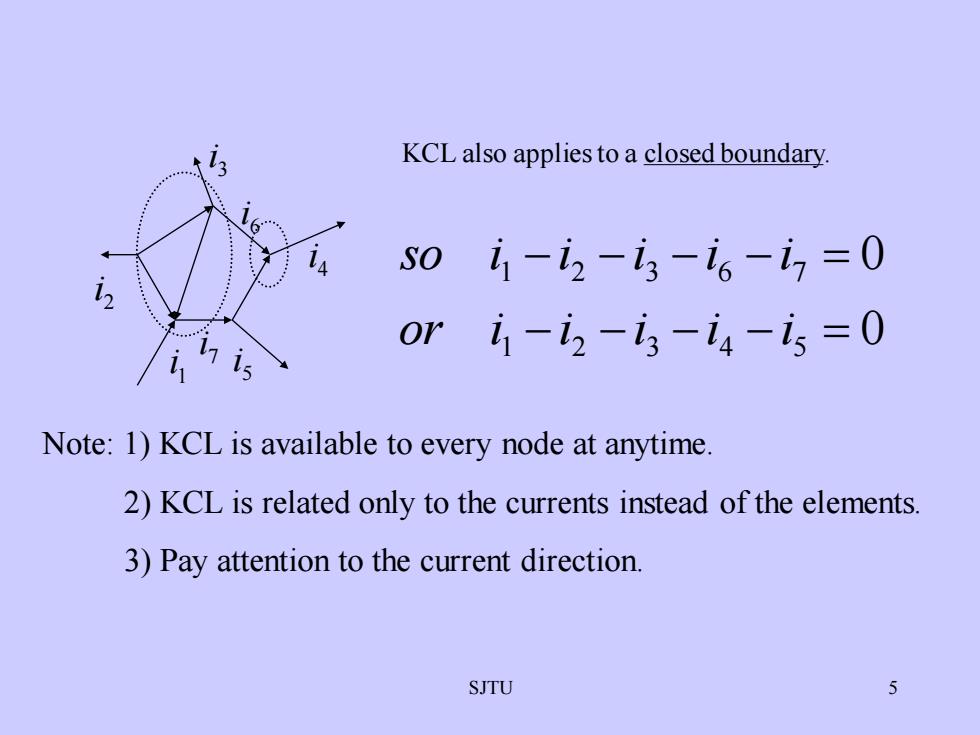
KCL also appliestoa closed boundaryso i-iz-is-ic-i =OOr i -iz -i -i4-is =ONote: 1)KCL is available to every node at anytime2)KCL is related only to the currents instead of the elements3) Pay attention to the current directionSJTU5
SJTU 5 KCL also applies to a closed boundary. 1 i 2 i 3 i 4 i 5 i 0 0 1 2 3 4 5 1 2 3 6 7 − − − − = − − − − = or i i i i i so i i i i i 7 i 6 i Note: 1) KCL is available to every node at anytime. 2) KCL is related only to the currents instead of the elements. 3) Pay attention to the current direction
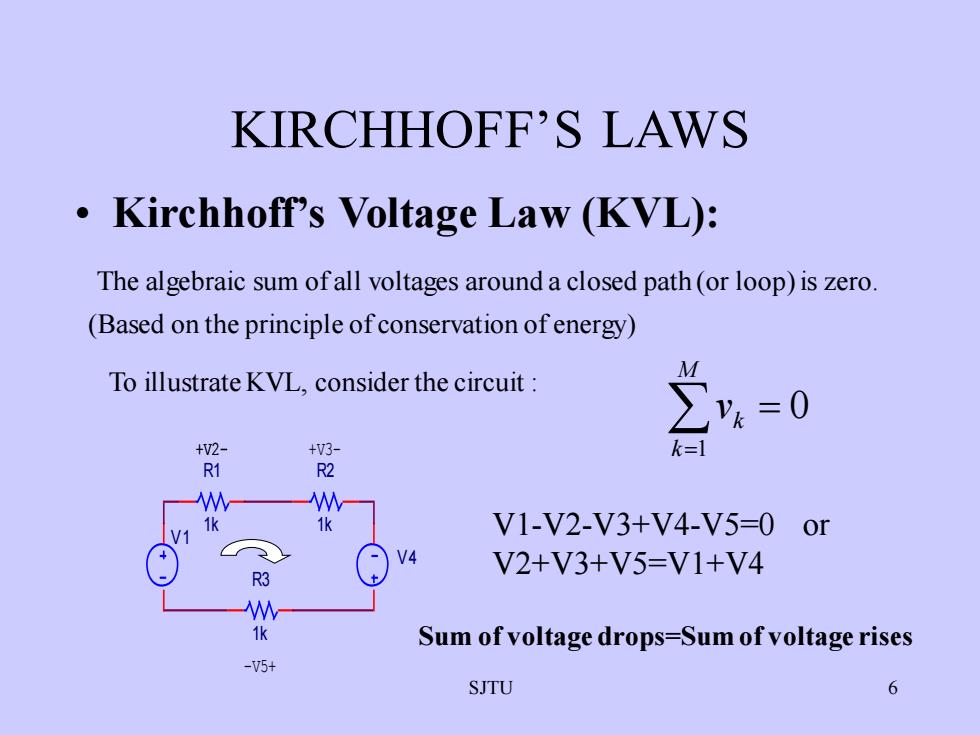
KIRCHHOFF'SLAWS.Kirchhoff's Voltage Law (KVL):The algebraic sum of all voltages around a closed path (or loop)is zero(Based on the principle of conservation of energy)MTo illustrateKVL,considerthecircuit :Z=0Vkk=l+V2+V3-R1R2W1k1kV1-V2-V3+V4-V5-0orV1+V4V2+V3+V5=V1+V4R3W1kSum of voltagedrops=Sumofvoltagerises-V5+6SJTU
SJTU 6 KIRCHHOFF’S LAWS • Kirchhoff’s Voltage Law (KVL): The algebraic sum of all voltages around a closed path (or loop)is zero. (Based on the principle of conservation of energy) To illustrate KVL, consider the circuit : +V2- R1 1k V 4 -V5+ R3 1k V 1 R2 1k +V3- V1-V2-V3+V4-V5=0 or V2+V3+V5=V1+V4 Sum of voltage drops=Sum of voltage rises = = M k k v 1 0

TWOSORTS OE CONSTRAINTS1.Topological constraintsDetermined by the way of connection among the elements.(Such asKCL KVL)2.Elementconstraints(VAR)Determined bythe elements.Using two sorts of constraints, we can analysis anylumped circuit (solve out all the voltages and currents)SJTU7
SJTU 7 TWO SORTS OF CONSTRAINTS • 1. Topological constraints Determined by the way of connection among the elements. (Such as KCL KVL) 2. Element constraints Determined by the elements. (VAR) Using two sorts of constraints, we can analysis any lumped circuit (solve out all the voltages and currents)

In a circuit with b branches and n nodes, there are 2b variables should bevalued.Then:KCLfor n nodes:onlyn-1 equationsareindependent.KVLfor loops:onlyb-n+1 equations are independent.(onlyKVLformeshes)VAR for branches: b equations.So,(n-1)+(b-n+1)+b=2b,2bequationstovalue2bvariablesThat is called 2b analysis8SJTU
SJTU 8 In a circuit with b branches and n nodes, there are 2b variables should be valued. Then: KCLfor n nodes: only n-1 equations are independent. KVL for loops: only b-n+1 equations are independent. (only KVL for meshes) VAR for branches: b equations. So, (n-1)+(b-n+1)+b=2b, 2b equationsto value 2b variables. That is called 2b analysis

SERIESRESISTORSANDVOLTAGEDIVISIONAs we know, Series-connected means that the same current flows inthem.The equivalent resistance of any number of resistors connected inseries is the sum ofthe individual resistancesSeeillustrationwith2resistorsV=Vi+V2=Ri+Ri=RiiRiR2M+:. R=R +R2V2V1R is the equivalent resistance.bIt can be applied to any number of resistors9SJTU
SJTU 9 SERIES RESISTORS AND VOLTAGE DIVISION • As we know, Series-connected means that the same current flows in them. • The equivalent resistance of any number of resistors connected in series is the sum of the individual resistances. See illustration with 2 resistors: 1 2 1 2 1 2 R R R v v v R i R i Ri = + = + = + = R is the equivalent resistance. It can be applied to any number of resistors

P=vi=vi+vi=Ri?+Ri= Ri? = P+ P2The equivalent powerof anynumberof resistors connectedin seriesis the sum oftheindividual powersConcept of Equivalent:Be equivalent to the outside, not the insidePrinciple of voltage division:if a voltage divider has Nresistors(Ri,R2,... Rn) in series with the source voltage Vthe nth resistor(Rn)will have a voltage drop ofRnVn2R, + R, +...+ Rn10SJTU
SJTU 10 Concept of Equivalent: Be equivalent to the outside, not the inside. Principle of voltage division: if a voltage divider has N resistors(R1,R2,.RN) in series with the source voltage v, the nth resistor(Rn)will have a voltage drop of 1 2 2 2 2 2 1 2 1 Ri P P P v i v i v i R i R i = = + = = + = + The equivalent power of any number of resistors connected in series is the sum of the individual powers. v R R R R v N n n + + + = . 1 2