
NANJING UNIVERSITY Timed Automata
Timed Automata

效绵鼎 Aim of the Lecture knowledge of a basic formalism for modeling timed systems basic understanding of verification algorithms for timed systems (useful for practical modeling and verification)
Aim of the Lecture ◼ knowledge of a basic formalism for modeling timed systems ◼ basic understanding of verification algorithms for timed systems (useful for practical modeling and verification)

效绵鼎 Example:Peterson's Algorithm flag[0],flag[1](initialed to false)-meaning I want to access CS turn (initialized to 0)-used to resolve conflicts Process 0: Process 1: while (true){ while (true){ ; ; flag[0]:true; flag[1]:true; turn :1; turn :0; while flag[1]and while flag[0]and turn =1 do {} turn =0 do; ; ; flag[o]:false; flag[1]:false;
Example: Peterson's Algorithm ◼ flag[0], flag[1] (initialed to false) — meaning I want to access CS ◼ turn (initialized to 0) — used to resolve conflicts Process 0: while (true) { ; flag[0] := true; turn := 1; while flag[1] and turn = 1 do { }; ; flag[0] := false; } Process 1: while (true) { ; flag[1] := true; turn := 0; while flag[0] and turn = 0 do { }; ; flag[1] := false; }
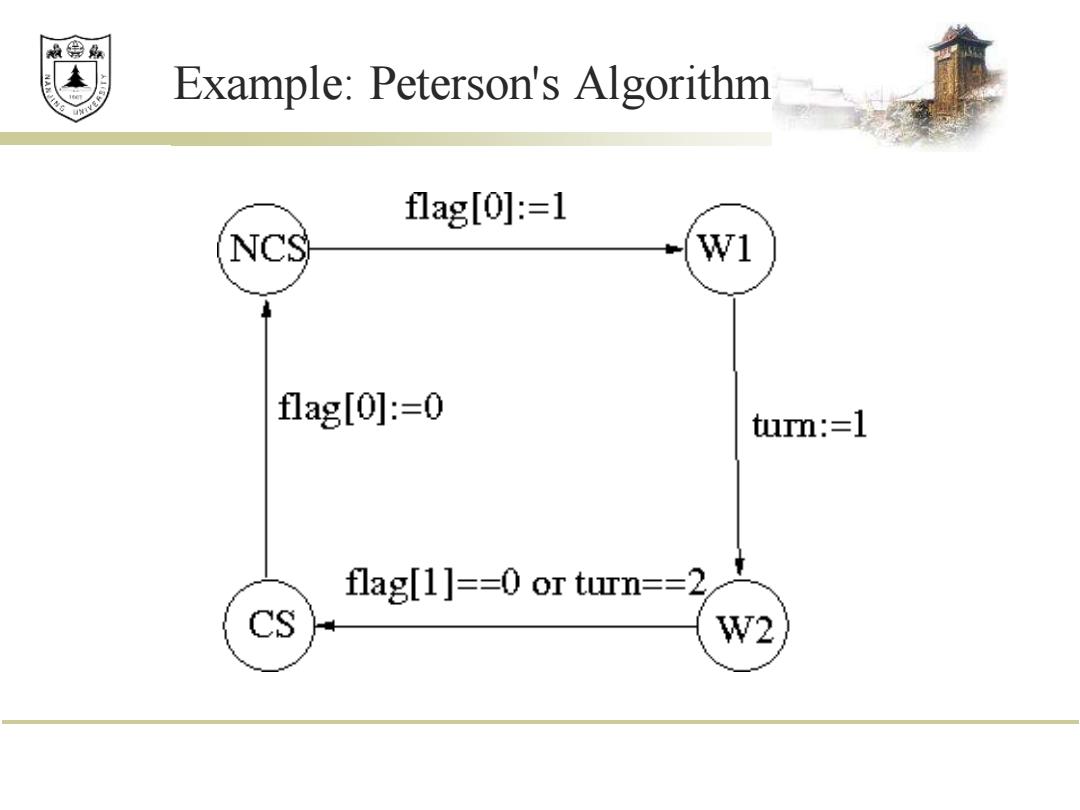
赖绵县 Example:Peterson's Algorithm flag[0]:=1 NCS w1 flag[0]小:=0 turn:=1 flag[1]==0 or turn==2 CS W2
Example: Peterson's Algorithm
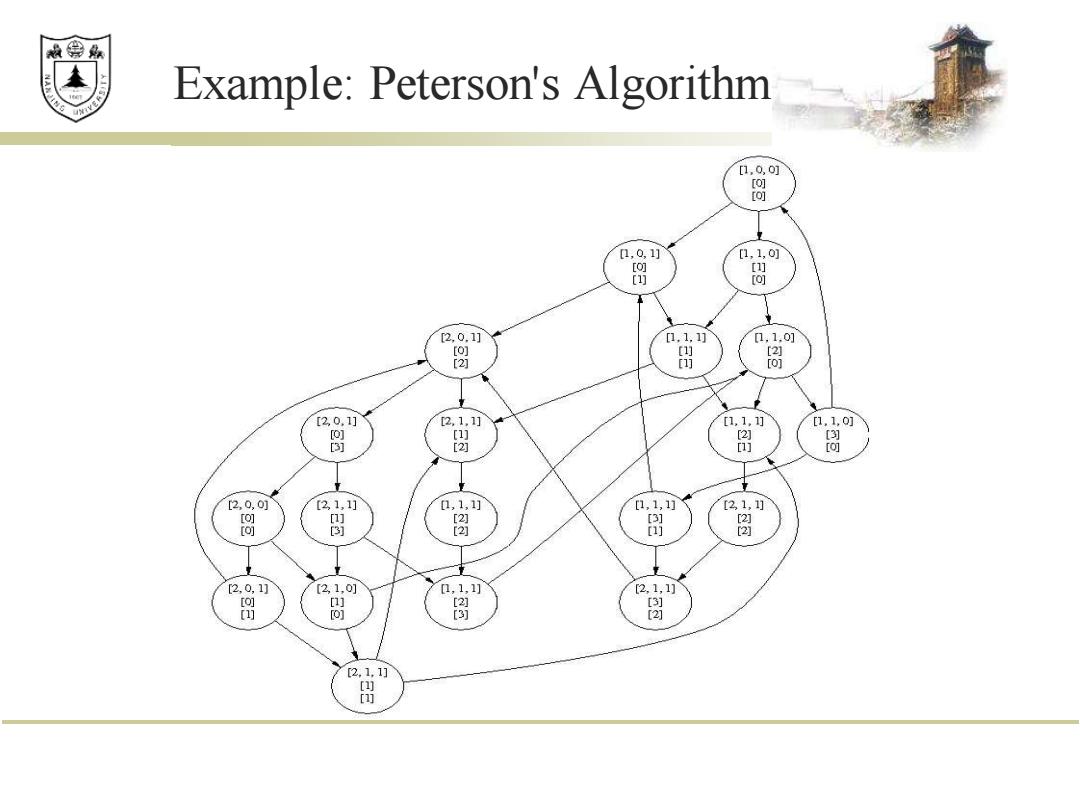
效绵鼎 Example:Peterson's Algorithm [1.0,0j [o] [o] 0,0,1] 1,1,0 [ [ [) [o] 2,0.1] [1,1,1 1,1.0] [O] [ [ [2] n [o] [2,0.1] 2,1.1] [1,1,1] [1,1,] [2 3) [3 [2 j [2,0,0j [2,1,1] 1,1,1] [1,1,1] 2,1,1] [o] [2 3 图 2 [20,1] [2,1,0] 1,1,1] [2,1,1 [o] [] [2☒ [ ] [o] [3) 2] [2,1,1] [ [
Example: Peterson's Algorithm

效绵鼎 Fischer's Protocol id -shared variable each process has it's own timer (for delaying) for correctness it is necessary that K2 >KI Process i: while (true){ ; while id !=0 do delay K1; id :i; delay K2; if (id =i){ ; id=0;
Fischer's Protocol ◼ id — shared variable ◼ each process has it's own timer (for delaying) ◼ for correctness it is necessary that K2 > K1 Process i: while (true) { ; while id != 0 do {} delay K1; id := i; delay K2; if (id = i) { ; id := 0; } }

效绵鼎 Modeling Real Time Systems Two models of time: 0 discrete time domain continuous time domain
Modeling Real Time Systems ◼ Two models of time: discrete time domain continuous time domain

效绵鼎 Discrete Time Domain clock ticks at regular interval at each tick something may happen between ticks-the system only waits
Discrete Time Domain ◼ clock ticks at regular interval ◼ at each tick something may happen ◼ between ticks — the system only waits

效绵 Discrete Time Domain choose a fixed sample period s all events happen at multiples of s simple extension of classical models main disadvantage -how to choose s bige→too coarse model o low 8=>time fragmentation,too big state space usage:particularly synchronous systems (hardware circuits)
Discrete Time Domain ◼ choose a fixed sample period ε ◼ all events happen at multiples of ε ◼ simple extension of classical models ◼ main disadvantage — how to choose ε ? big ε too coarse model low ε time fragmentation, too big state space ◼ usage: particularly synchronous systems (hardware circuits)

效绵 Continuous Time Domain time is modeled as real numbers delays may be arbitrarily small more faithful model,suited for asynchronous systems uncountable state space =cannot be directly handled automatically by "brute force
Continuous Time Domain ◼ time is modeled as real numbers ◼ delays may be arbitrarily small ◼ more faithful model, suited for asynchronous systems ◼ uncountable state space cannot be directly handled automatically by “brute force