
Control Flow:Representation,Extraction and Applications
Control Flow: Representation, Extraction and Applications

Program needs a representation for the analysis 1 #include 2 int main(){ 3 printf("pid=%d\n",getpid()); 4 return 0; 5} c17f093d: 55 push %ebp c17f093e: 89e5 mov %esp,%ebp c17f0940: 83ec08 sub $0x8,%esp c17f0943: e8402d81ff call c1003688 Original representations Source code(cross languages). Binaries (cross machines and platforms). >Source code binaries test cases. They are hard for machines to analyze. ● Software is translated into certain representation before analyses are applied. 2
2 Program needs a representation for the analysis • Original representations ➢ Source code(cross languages). ➢ Binaries (cross machines and platforms). ➢ Source code / binaries + test cases. • They are hard for machines to analyze. • Software is translated into certain representation before analyses are applied. 1 #include 2 int main(){ 3 printf("pid=%d\n",getpid()); 4 return 0; 5 } c17f093d: 55 push %ebp c17f093e: 89 e5 mov %esp,%ebp c17f0940: 83 ec 08 sub $0x8,%esp c17f0943: e8 40 2d 81 ff call c1003688
Outline Static Program Representation >Control Flow Graph Program Dependence Graph >Points-to Graph >Call Graph Control Flow Graph Extraction >Source Code to CFG >ELF/PE File to CFG 。Applications >Control Flow Integrity -Principles and Implementations(CFI) >Practical Control Flow Integrity Randomization for Binary Executables(CCFIR) ●Summary 3
3 Outline • Static Program Representation ➢ Control Flow Graph ➢ Program Dependence Graph ➢ Points-to Graph ➢ Call Graph • Control Flow Graph Extraction ➢ Source Code to CFG ➢ ELF/PE File to CFG • Applications ➢ Control Flow Integrity – Principles and Implementations(CFI) ➢ Practical Control Flow Integrity & Randomization for Binary Executables(CCFIR) • Summary
Outline Static Program Representation >Control Flow Graph Program Dependence Graph >Points-to Graph >Call Graph Control Flow Graph Extraction >Source Code to CFG ELF/PE File to CFG 。Applications >Control Flow Integrity -Principles and Implementations(CFI) Practical Control Flow Integrity Randomization for Binary Executables(CCFIR) ●Summary 4
4 Outline • Static Program Representation ➢ Control Flow Graph ➢ Program Dependence Graph ➢ Points-to Graph ➢ Call Graph • Control Flow Graph Extraction ➢ Source Code to CFG ➢ ELF/PE File to CFG • Applications ➢ Control Flow Integrity – Principles and Implementations(CFI) ➢ Practical Control Flow Integrity & Randomization for Binary Executables(CCFIR) • Summary

Basic Blocks ●Definition A basic block is a maximal sequence of consecutive statements with a single entry point, a single exit point,and no internal branches Control always enters a basic block at its entry point and exits from its exit point.There is no possibility of exit or a halt at any point inside the basic block except at its exit point.The entry and exit points of a basic block coincide when the block contains only one statement. 5
5 Basic Blocks • Definition ➢ A basic block is a maximal sequence of consecutive statements with a single entry point, a single exit point, and no internal branches • Control always enters a basic block at its entry point and exits from its exit point. There is no possibility of exit or a halt at any point inside the basic block except at its exit point. The entry and exit points of a basic block coincide when the block contains only one statement

Basic Block Example (1) i=m-1 (2) j:=n How many basic blocks in this code (3) t1=4*n fragment? (4) v:=a[t1] (5) i:=i+1 What are they? (6) t2:=4*1 (7) t3:=a[t2] (8) if t3v goto (9) (13) if i>=j goto(23) (14) t6=4*1 (15) x:=a[t6] 6
6 Basic Block Example (1) i := m-1 (2) j := n (3) t1 := 4 * n (4) v := a[t1] (5) i := i + 1 (6) t2 := 4 * I (7) t3 := a[t2] (8) if t3 v goto (9) (13) if i >= j goto (23) (14) t6 := 4 * I (15) x := a[t6] … • How many basic blocks in this code fragment? • What are they?

Basic Block Example (1) i=m-1 (2) j:=n How many basic blocks in this code (3) t1=4*n fragment? (4) v:=a[t1] (5) i=1+1 What are they? (6) t2:=4*1 (7) t3:=a[t2] (8) if t3=jgoto(23) (14) t6:=4*1 (15) x:=a[t6]
7 Basic Block Example (1) i := m-1 (2) j := n (3) t1 := 4 * n (4) v := a[t1] (5) i := i + 1 (6) t2 := 4 * I (7) t3 := a[t2] (8) if t3 v goto (9) (13) if i >= j goto (23) (14) t6 := 4 * I (15) x := a[t6] … • How many basic blocks in this code fragment? • What are they?
Basic Block Example 1 begin A list of all basic blocks in the program is 2 int x,y,power; 3 float z; given below. 4 input (x,y); Block Lines Entry Point Exit Point 5 if (y<0) 6 power=y; 1 2,3,4,5 1 5 7 else 2 6 6 6 8 power=y; 3 8 8 8 9 2=1; 10 while(power!=0){ 4 9 9 9 11 2=z*X) 5 10 10 10 12 power=power-1; 6 11,12 11 12 13 } 14 if (y<0) 7 14 14 14 15 Z=1/z; 8 15 15 15 16 output (z); 9 16 16 16 17 end 8
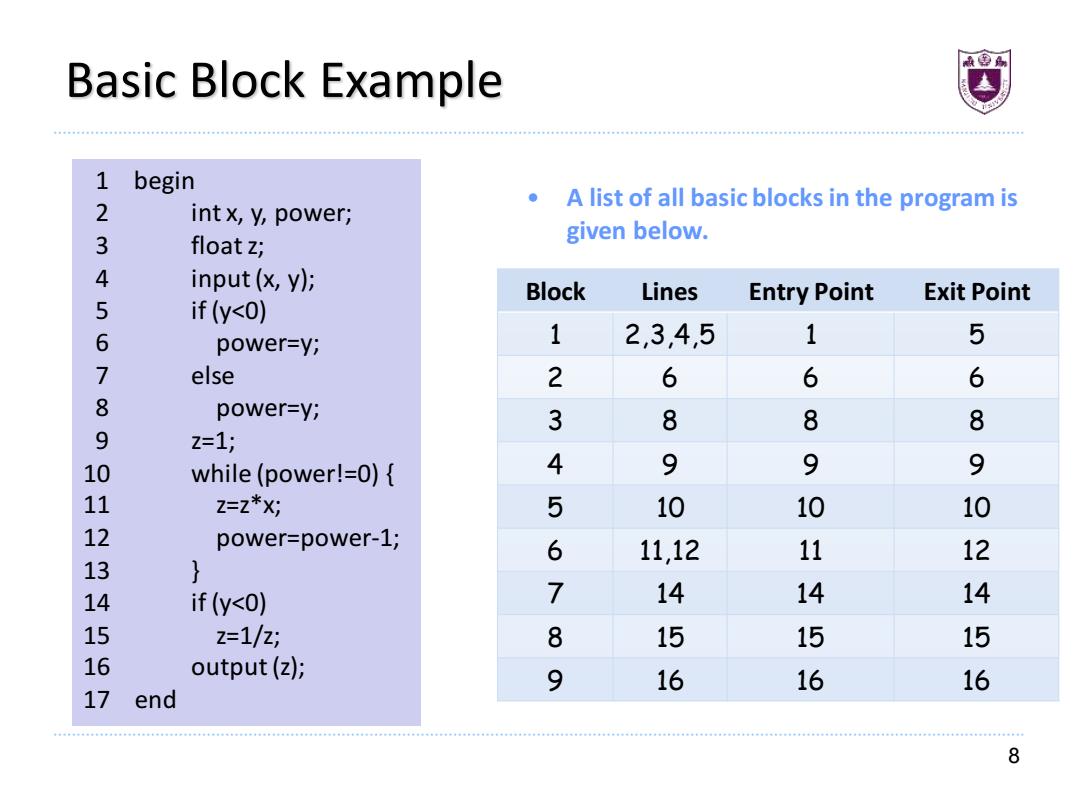
8 Basic Block Example 1 begin 2 int x, y, power; 3 float z; 4 input (x, y); 5 if (y<0) 6 power=y; 7 else 8 power=y; 9 z=1; 10 while (power!=0) { 11 z=z*x; 12 power=power-1; 13 } 14 if (y<0) 15 z=1/z; 16 output (z); 17 end • A list of all basic blocks in the program is given below. Block Lines Entry Point Exit Point 1 2,3,4,5 1 5 2 6 6 6 3 8 8 8 4 9 9 9 5 10 10 10 6 11,12 11 12 7 14 14 14 8 15 15 15 9 16 16 16

Control Flow Graph A control flow graph (or flow graph)G is defined as a finite set N of nodes and a finite set E of edges.An edge(i,j)in E connects two nodes ni and nj in N.We often write G=(N,E)to denote a flow Graph G with nodes given by N and edges by E. .G=(N,E)as a directed graph Node n E N:basic blocks A basic block is a maximal sequence of stmts with a single entry point,single exit point,and no internal branches For simplicity,we assume a unique entry node no and a unique exit node n in later discussions Edge e=(ni,nj)EE:possible transfer of control from block ni to block nj We also assume that there is a node labeled Start in N that has no incoming edge,and another node labeled End,also in N,that has no outgoing edge. 9
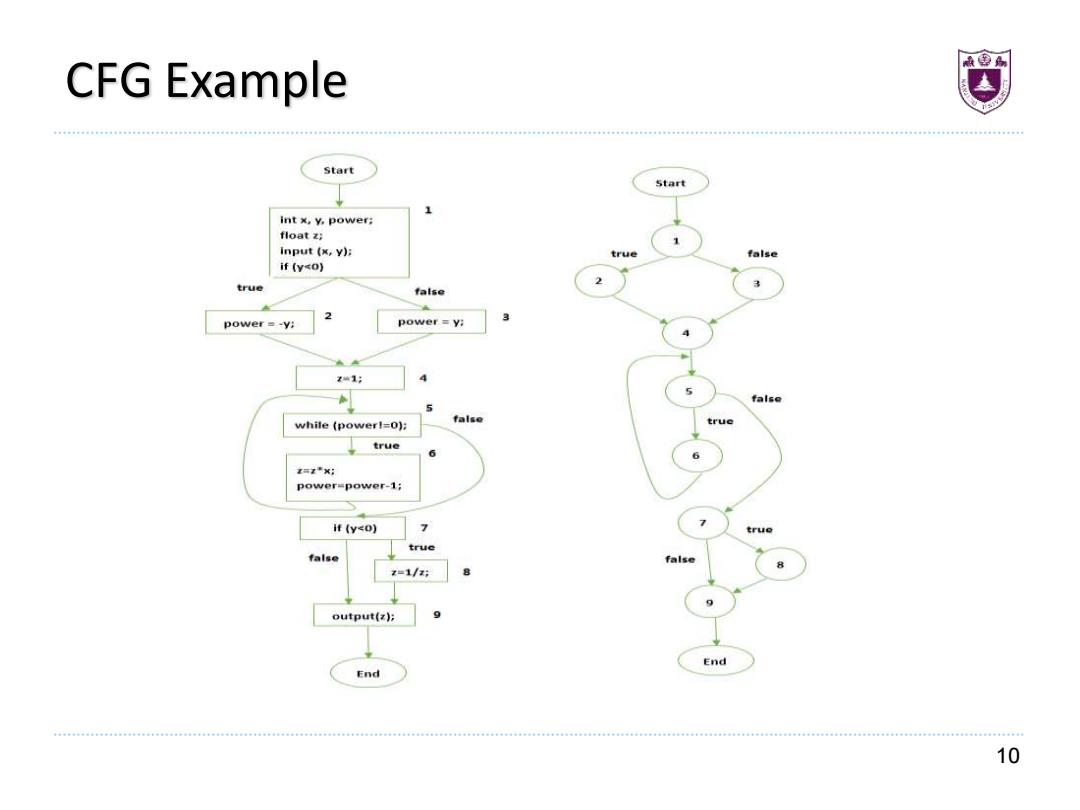
9 Control Flow Graph • A control flow graph (or flow graph) G is defined as a finite set N of nodes and a finite set E of edges. An edge (i, j) in E connects two nodes 𝑛𝑖 and 𝑛𝑗 in N. We often write G=(N, E) to denote a flow Graph G with nodes given by N and edges by E. • G = (N, E) as a directed graph ➢ Node n ∈ N: basic blocks ✓ A basic block is a maximal sequence of stmts with a single entry point, single exit point, and no internal branches ✓ For simplicity, we assume a unique entry node 𝑛0 and a unique exit node 𝑛𝑓 𝑖𝑛 𝑙𝑎𝑡𝑒𝑟 𝑑𝑖𝑠𝑐𝑢𝑠𝑠𝑖𝑜𝑛𝑠 ➢ Edge e = (𝑛𝑖 , 𝑛𝑗 ) ∈ E: possible transfer of control from block 𝑛𝑖 to block 𝑛𝑗 • We also assume that there is a node labeled Start in N that has no incoming edge, and another node labeled End, also in N, that has no outgoing edge
CFG Example Start Start int x,y.power: float z: input《,yH true false if (y<o) true false 3 power =-y; 2 power y: 1地1: false 5 while (powerl=0); false true true =z*×: power-power-1: if (y<o) true true false false x=1/x: output(z): End End 10
10 CFG Example