
第3章 公钥密码体系与密钥管理 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 第3章 公钥密码体系与密钥管理

密钥管理 Problem: n users.Storing mutual secret keys is difficult Total:O(n)keys per user
密钥管理 Problem: n users. Storing mutual secret keys is difficult Total: O(n) keys per user

为什么需要公钥密码体系? 在网络通信中,使用对称密码算法加密数据时,通信各方必须首 先协商好所使用的秘密密钥 通过专人传送秘密密钥 通过开会的方式确定秘密密钥 使用邮寄、E-mail以及电话等方式传送秘密密钥 口 但是,这些传统的方式不能适应现代网络通信的需要 公钥密码体系(PKC) 0 于1970年代出现 能够在没有预先共享秘密密钥的情况下进行安全的密钥分发 口用于身份鉴别 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 为什么需要公钥密码体系? 在网络通信中,使用对称密码算法加密数据时,通信各方必须首 先协商好所使用的秘密密钥 通过专人传送秘密密钥 通过开会的方式确定秘密密钥 使用邮寄、E-mail以及电话等方式传送秘密密钥 … 但是,这些传统的方式不能适应现代网络通信的需要 公钥密码体系(PKC) 于1970年代出现 能够在没有预先共享秘密密钥的情况下进行安全的密钥分发 用于身份鉴别

第3章内容概要 ●3.1公钥密码体系的定义 ●3.2数论的基本概念和定理 ●3.3 Diffie-Hellman密钥交换 ●3.4RSA密码体系 ●3.5椭圆曲线密码体系 ●3.6密钥分配与管理 《计算机网络安全的理论与实践(第2版)》.【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 第3章 内容概要 3.1 公钥密码体系的定义 3.2 数论的基本概念和定理 3.3 Diffie-Hellman密钥交换 3.4 RSA 密码体系 3.5 椭圆曲线密码体系 3.6 密钥分配与管理
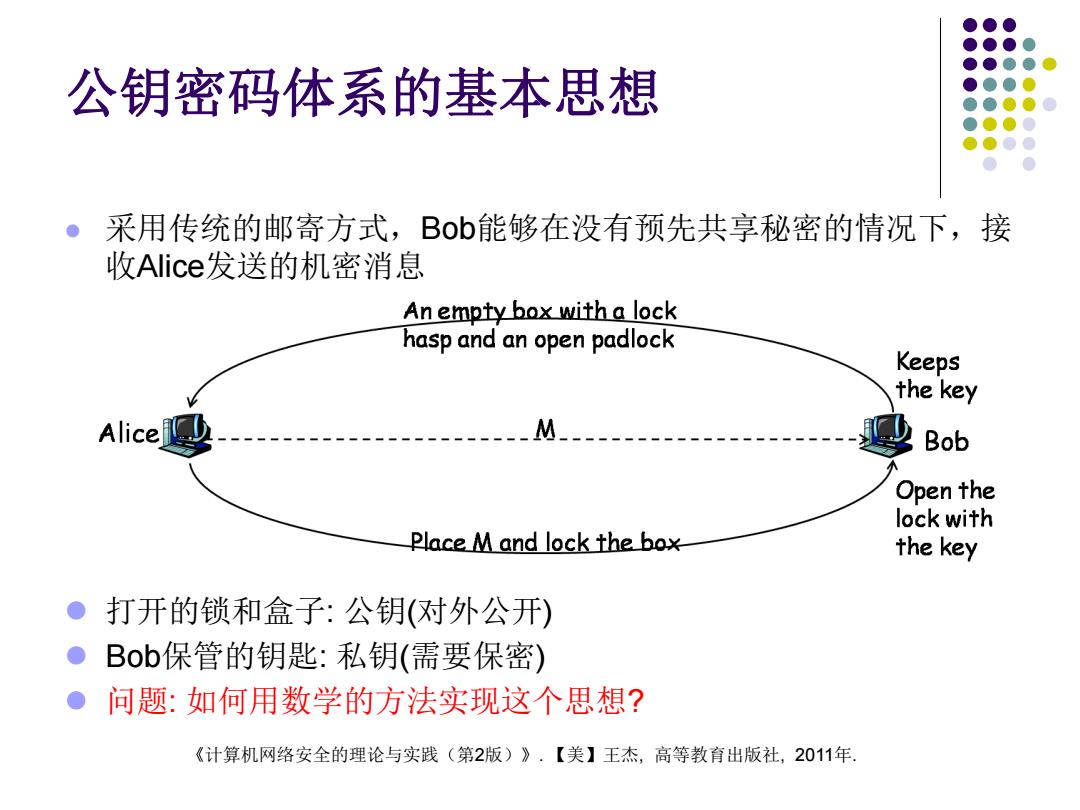
公钥密码体系的基本思想 ● 采用传统的邮寄方式,Bob能够在没有预先共享秘密的情况下,接 收Alice发送的机密消息 An empty box with a lock hasp and an open padlock Keeps the key Alice --M- Bob Open the lock with Place M and lock the box the key ●打开的锁和盒子:公钥(对外公开) ●Bob保管的钥匙:私钥(需要保密) ●问题:如何用数学的方法实现这个思想? 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 公钥密码体系的基本思想 采用传统的邮寄方式,Bob能够在没有预先共享秘密的情况下,接 收Alice发送的机密消息 打开的锁和盒子: 公钥(对外公开) Bob保管的钥匙: 私钥(需要保密) 问题: 如何用数学的方法实现这个思想?

另一个例子 ● 假设存在两个函数6和f,满足f(a,),x)=f(a,x),y),而且, 通过已知的f6(a,x)和a很难计算出x ●Aice进行以下步骤: 0【 随机选取一个正整数x1(私钥),然后发送y=f(a,x1)给Bob ·类似的,Bob进行以下步骤: ▣} 随机选取一个正整数x2(私钥),然后发送y2=f(a,x2)给Alice ● Bob计算K2=fy1,x2),Alice计算K=fO2,x1),作为他们的秘密 密钥 ● 因为f0y2,x1)=ff(a,x2),x1)=ff(a,x1),x2)=f0y1,x2),因此有 K=K2 Malice可以在通信线路上监听到y1andy2,但是不能获得x,orx2 问题:如何找到这样的函数f和? 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 另一个例子 假设存在两个函数f0和f1,满足f1 (f0 (a, y), x) = f1 (f0 (a, x), y) ,而且, 通过已知的f0 (a, x) 和a很难计算出x Alice进行以下步骤: 随机选取一个正整数x1 (私钥),然后发送y1 = f0 (a, x1 ) 给Bob 类似的,Bob 进行以下步骤: 随机选取一个正整数x2 (私钥) ,然后发送 y2 = f0 (a, x2 ) 给Alice Bob 计算 K2= f1 (y1 , x2 ),Alice 计算 K1= f1 (y2 , x1 ) ,作为他们的秘密 密钥 因为 f1 (y2 , x1 ) = f1 (f0 (a, x2 ), x1 ) = f1 (f0 (a, x1 ), x2 ) = f1 (y1 , x2 ), 因此有 K1= K2 Malice 可以在通信线路上监听到y1 and y2 , 但是不能获得x1 or x2 问题: 如何找到这样的函数f1和f2?

公钥密码体系的准侧 。正向计算易解性 口计算加密和解密是容易的 口产生一对密钥对(Ku,K9是容易的,其中Ku是公钥,K是对应的私钥 。反向计算难解性 口通过密文C和公钥Ku计算明文M是计算难解的 口公钥Ku不能泄露关于私钥K的有用信息 ·可交换性 (K,K9满足 M D(E(M ))=D(E(M)) =E(D (M ))=E(D(M)) 口对身份验证和数字签名是需要的,但对于密钥交换不是必需的 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 公钥密码体系的准则 正向计算易解性 计算加密和解密是容易的 产生一对密钥对(Ku , Kr ) 是容易的,其中 Ku 是公钥,Kr 是对应的私钥 反向计算难解性 通过密文 C 和公钥 Ku 计算明文M是计算难解的 公钥Ku 不能泄露关于私钥Kr的有用信息 可交换性 (Ku , Kr ) 满足 对身份验证和数字签名是需要的,但对于密钥交换不是必需的

第3章内容概要 ●3.1公钥密码体系的定义 ●3.2数论的基本概念和定理 ●3.3 Diffie-Hellman密钥交换 ●3.4RSA密码体系 ●3.5椭圆曲线密码体系 ●3.6密钥分配与管理 《计算机网络安全的理论与实践(第2版)》.【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 第3章 内容概要 3.1 公钥密码体系的定义 3.2 数论的基本概念和定理 3.3 Diffie-Hellman密钥交换 3.4 RSA 密码体系 3.5 椭圆曲线密码体系 3.6 密钥分配与管理

·算数基本定理 口任意大于1的整数都可表示为若干个素数的乘积。而 且,如果这些素数按非降序排列的话,这种表示是 唯一的。 n=p11p22…p4, p<p2<...<p,are prime numbers, a,(i=1,...,t)is a positive integer ·素数定理 口设n是大于1的整数,π(n)表示小于n的素数的个数, 则 π(m)~n/lnn 《计算机网络安全的理论与实践(第2版)》·【美】王杰,高等教育出版社,2011年
《计算机网络安全的理论与实践(第2版)》. 【美】王杰, 高等教育出版社, 2011年. 算数基本定理 任意大于1的整数都可表示为若干个素数的乘积。而 且,如果这些素数按非降序排列的话,这种表示是 唯一的。 素数定理 设 n 是大于1的整数,π(n) 表示小于n的素数的个数, 则 π(n) ~ n/ln n

Facts About Numbers Prime number p: ▣p is an integer p≥2 The only divisors of p are 1 and p ●Examples ▣2,7,l9 are primes -3,0,1,6 are not primes Prime decomposition of a positive integer n: n=p1e1×.Xpxk ●Example: 口200=23×52 Fundamental Theorem of Arithmetic The prime decomposition of a positive integer is unique 3/31/2016 Cryptography 11
Facts About Numbers Prime number p: p is an integer p 2 The only divisors of p are 1 and p Examples 2, 7, 19 are primes -3, 0, 1, 6 are not primes Prime decomposition of a positive integer n: n = p1 e 1 … pk e k Example: 200 = 2 3 5 2 Fundamental Theorem of Arithmetic The prime decomposition of a positive integer is unique 3/31/2016 Cryptography 11