
UQSTC 4的 /956 第五章 图像复原 电子科技大学自动化学院
第五章 图像复原 电子科技大学自动化学院

/966 W1-CONFIG 1/0,IRQ.RAH 280,3,D0000 00,18,CC000 2-ROM-ADORES NONE/SOFTE 丽08000 离焦形成的模糊 原始图像 如何恢复 运动形成的模糊 原始图像
如何恢复 离焦形成的模糊 原始图像 运动形成的模糊 原始图像

图像复原目的: /966 尽量减少或去除获取图像或处理图 像过程中的图像降质(图像退化),恢 复其本来面目。 图象退化的主要表现形式: 图像模糊;图像受到干扰
图像复原目的: 尽量减少或去除获取图像或处理图 像过程中的图像降质(图像退化),恢 复其本来面目。 图象退化的主要表现形式: 图像模糊;图像受到干扰
光学系 /956 统中的 传感器 衍射 非线性 畸变 光学系 统的像 差 产生原因 几何 畸变 摄影胶 片的非 线性 大气流 对象运 亚采样 的扰动 动造成 效应 的模糊
产生原因 光学系 统中的 衍射 传感器 非线性 畸变 光学系 统的像 差 摄影胶 片的非 线性 大气流 的扰动 效应 对象运 动造成 的模糊 几何 畸变 亚采样

图像复原方法: /966 找到降质或退化的原因,分析引起降质 或退化的因素,建立相应的数学模型, 并沿着图像降质的逆过程恢复图像。 图像退化模型决定图像复原效果
图像复原方法: 找到降质或退化的原因,分析引起降质 或退化的因素,建立相应的数学模型, 并沿着图像降质的逆过程恢复图像。 图像退化模型决定图像复原效果

图像复原和图像增强的区别: /966 图像增强不考虑图像是如何退化的,而是 试图采用各种技术来增强图像的视觉效果。 图像复原需知道图像退化的机制和过程等 先验知识,并据此找出一种相应的逆处理 方法,从而得到复原的图像。 ■二者的目的都是为了改善图像的质量
图像复原和图像增强的区别: 图像增强不考虑图像是如何退化的,而是 试图采用各种技术来增强图像的视觉效果。 图像复原需知道图像退化的机制和过程等 先验知识,并据此找出一种相应的逆处理 方法,从而得到复原的图像。 二者的目的都是为了改善图像的质量

>5.1图像退化的数学模型 目录 CONTENTS >5.2噪声模型 >5.3噪声估计 >5.4退化函数估计 >5.5无约束图像恢复 >5.6有约束图像恢复
目录 CONTENTS 5.1 图像退化的数学模型 5.2 噪声模型 5.3 噪声估计 5.4 退化函数估计 5.5 无约束图像恢复 5.6 有约束图像恢复

5.1图象退化的数学模型 /966 成像过程中的“退化”, 是指由于成像系统 各种因素的影响,使得图像质量降低。 退化模型:退化过程可以被模型化为一个退化函 数和一个噪声项。可以用连续数学模型描述,也 可以用离散数学模型描述
成像过程中的“退化”,是指由于成像系统 各种因素的影响,使得图像质量降低。 退化模型:退化过程可以被模型化为一个退化函 数和一个噪声项。可以用连续数学模型描述,也 可以用离散数学模型描述。 5.1 图象退化的数学模型
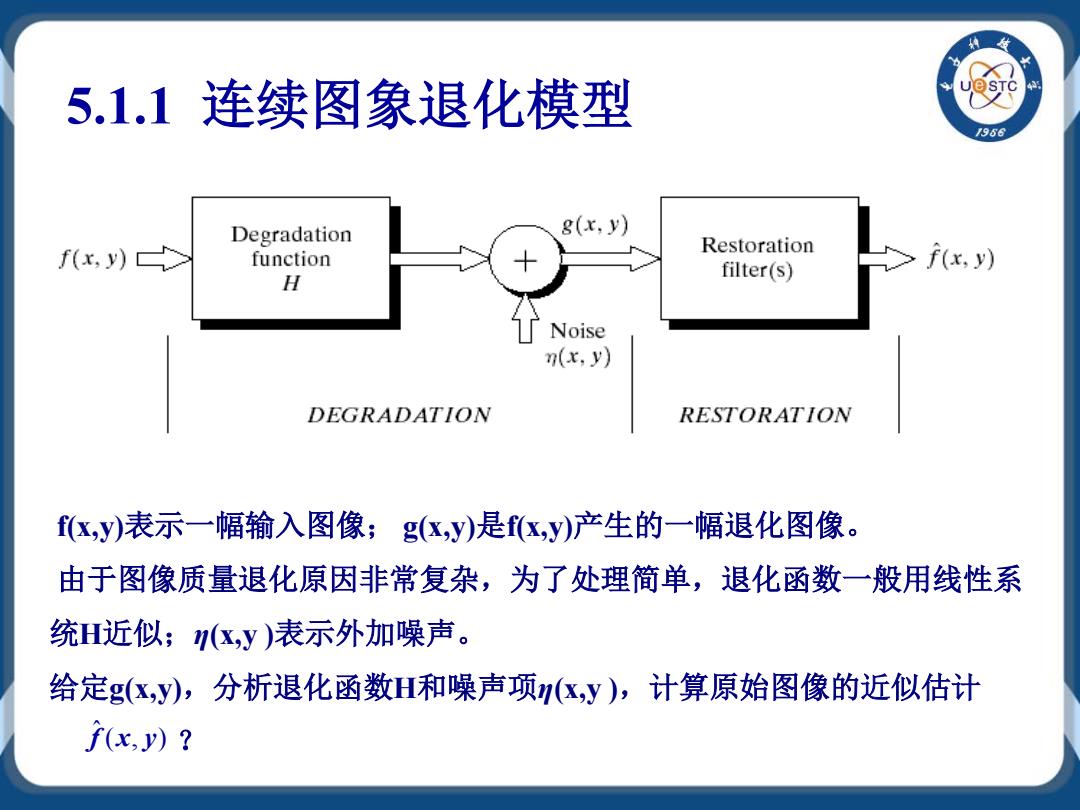
5.1.1 连续图象退化模型 STC /96 Degradation g(x,y) Restoration f(x,y) function f(x,y) H filter(s) Noise n(x,y) DEGRADATION RESTORATION f,y)表示一幅输入图像;gK,y)是fK,y)产生的一幅退化图像。 由于图像质量退化原因非常复杂,为了处理简单,退化函数一般用线性系 统H近似;k,y)表示外加噪声。 给定g(x,y),分析退化函数H和噪声项区,y),计算原始图像的近似估计 f(x,y)
5.1.1 连续图象退化模型 f(x,y)表示一幅输入图像; g(x,y)是f(x,y)产生的一幅退化图像。 由于图像质量退化原因非常复杂,为了处理简单,退化函数一般用线性系 统H近似;η(x,y )表示外加噪声。 给定g(x,y),分析退化函数H和噪声项η(x,y ),计算原始图像的近似估计 f ˆ(x, y) ?

线性系统H的性质: 1966 ()线性: H(xy)+k2f(xy)kH[f(x,y)]+k2H [f2(x,y)] (2)相加性(k1=k2=1): H[f(x,y)+f(x,y)]=H [f (x,y)+H [f(x,y)] (3)一致性(f化,y)=0): H(xy)=k H [f(x.y). (4)位置(空间)不变性: Hf(x-a,y-b)=g(x-a,y-b)
线性系统H的性质: (1) 线性: (2) 相加性(k1 = k2 = 1 ): (3) 一致性(f2(x, y) = 0 ): (4) 位置(空间)不变性: [ ( , ) ( , )] [ ( , )] [ ( , )] 1 1 2 2 1 1 2 2 H k f x y + k f x y = k H f x y + k H f x y [ ( , ) ( , )] [ ( , )] [ ( , )] 1 2 1 2 H f x y + f x y = H f x y + H f x y [ ( , )] [ ( , )] 1 1 1 1 H k f x y = k H f x y H [f (x − a, y − b)] = g(x − a, y − b)