
Background: Distributed Systems Synchronization/Logical time/Happens-before Consistency(Asynchronized Communication) Fault Tolerance(redundancy/k fault tolerant) distributed consensus
Background: Distributed Systems Synchronization/Logical time/Happens-before Consistency( Asynchronized Communication) Fault Tolerance(redundancy/k fault tolerant) distributed consensus

Problem description(distributed consensus) Consider a set of n isolated processors,of which it is known t that no more than m are faulty.It is not known,however,which processors are faulty.Suppose that the processors can commumcate only by means of two-party messages.The communication medium is presumed to be fail-safe and of negligible delay.The sender of a message,moreover,is always identifiable by the receiver.Suppose also that each processor p has some private value of information Vp(such as its clock value or its reading of some sensor). The question is whether for given m,n>0,it is possible to devise an algorithm based on an exchange of messages that will allow each nonfaulty processor)to compute a vector of values with an element for each of the n processors,such that
Problem description(distributed consensus) Consider a set of n isolated processors, of which it is known that no more than m are faulty. It is not known, however, which processors are faulty. Suppose that the processors can commumcate only by means of two-party messages. The communication medium is presumed to be fail-safe and of negligible delay. The sender of a message, moreover, is always identifiable by the receiver. Suppose also that each processor p has some private value of information Vp (such as its clock value or its reading of some sensor). The question is whether for given m, n > 0, it is possible to devise an algorithm based on an exchange of messages that will allow each nonfaulty processor) to compute a vector of values with an element for each of the n processors, such that

(1)the nonfaulty processors compute exactly the same vector, (2)the element of this vector corresponding to a given nonfaulty processor is the private value of that processor Interactive Consistency(IC)
(1) the nonfaulty processors compute exactly the same vector; (2) the element of this vector corresponding to a given nonfaulty processor is the private value of that processor. Interactive Consistency(IC)

The generals must have an algorithm to guarantee that: A.All loyal generals decide upon the same plan of action. A small number of traitors cannot cause the loyal generals to adopt a bad plan
The generals must have an algorithm to guarantee that: • A. All loyal generals decide upon the same plan of action. • A small number of traitors cannot cause the loyal generals to adopt a bad plan

For condition A to be satisfied,the following must be true: 1.Every loyal general must obtain the same information v (1)....,v (n). 2.If the ith general is loyal,then the value that he sends must be used by every loyal general as the value of v (i)
For condition A to be satisfied, the following must be true: • 1. Every loyal general must obtain the same information v (1) . . . . , v (n). • 2. If the ith general is loyal, then the value that he sends must be used by every loyal general as the value of v (i)

We can rewrite condition I as the condition that for every i (whether or not the ith general is loyal): 1'.Any two loyal generals use the same value of v(i)
We can rewrite condition I as the condition that for every i (whether or not the ith general is loyal): • 1'. Any two loyal generals use the same value of v(i)

Byzantine Generals Problem. A commanding general must send an order to his n-1 lieutenant generals such that IC1.All loyal lieutenants obey the same order. IC2.If the commanding general is loyal, then every loyal lieutenant obeys the order he sends
• Byzantine Generals Problem. A commanding general must send an order to his n - 1 lieutenant generals such that • IC1. All loyal lieutenants obey the same order. • IC2. If the commanding general is loyal, then every loyal lieutenant obeys the order he sends

n processes,m faulty n3m m+1 rounds/intuition perceptual knowledge/examples algorithms proofs
n processes, m faulty n3m m+1 rounds/intuition perceptual knowledge/examples algorithms proofs
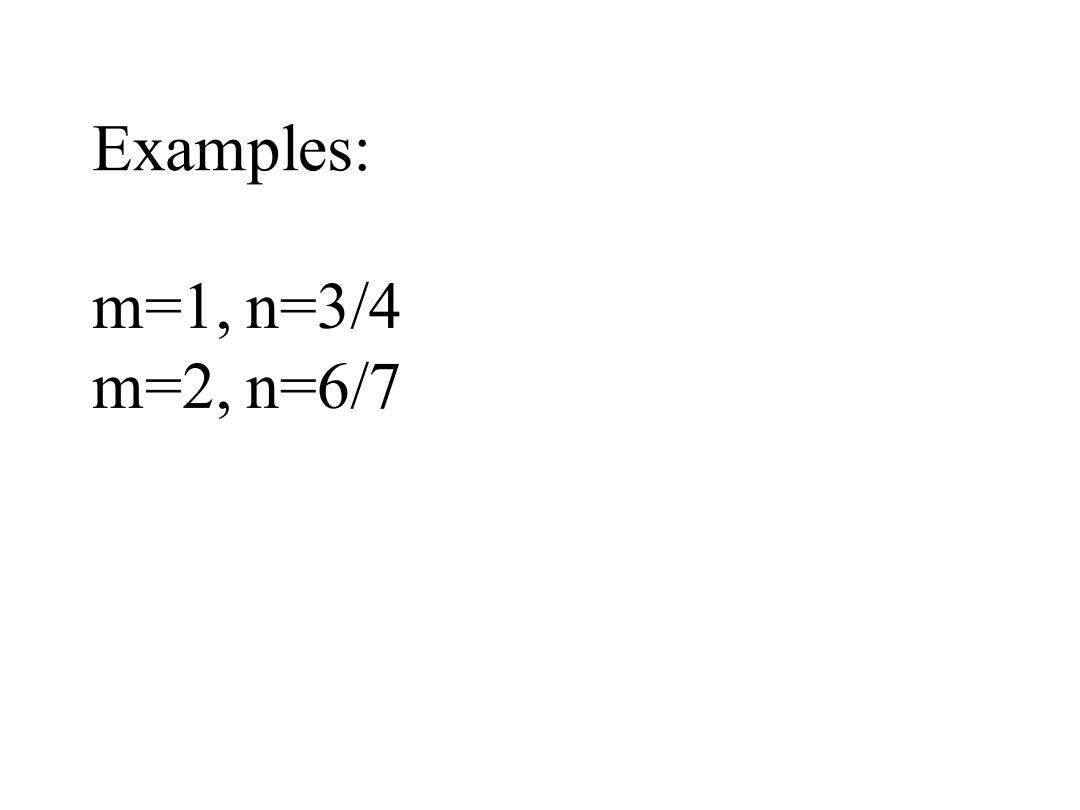
Examples: m=1,n=3/4 m=2,n=6/7
Examples: m=1, n=3/4 m=2, n=6/7

Slight Reformulation Structure problem as follows: Single element of the total communication Single commanding general Collection of receiving lieutenants Each might be a traitor Commander Lieutenant 1 Lieutenant 2