
NANJING UNIVERSITY Turing Machine Turing Machines Recursive and Recursively Enumerable Languages .1
Turing Machines Recursive and Recursively Enumerable Languages Turing Machine 1

效绵鼎 Turing-Machine Theory The purpose of the theory of Turing machines is to prove that certain specific languages s have no algorithm. Start with a language about Turing machines themselves. ■ Reductions are used to prove more common questions undecidable 2
Turing-Machine Theory ◼ The purpose of the theory of Turing machines is to prove that certain specific languages have no algorithm. ◼ Start with a language about Turing machines themselves. ◼ Reductions are used to prove more common questions undecidable. 2
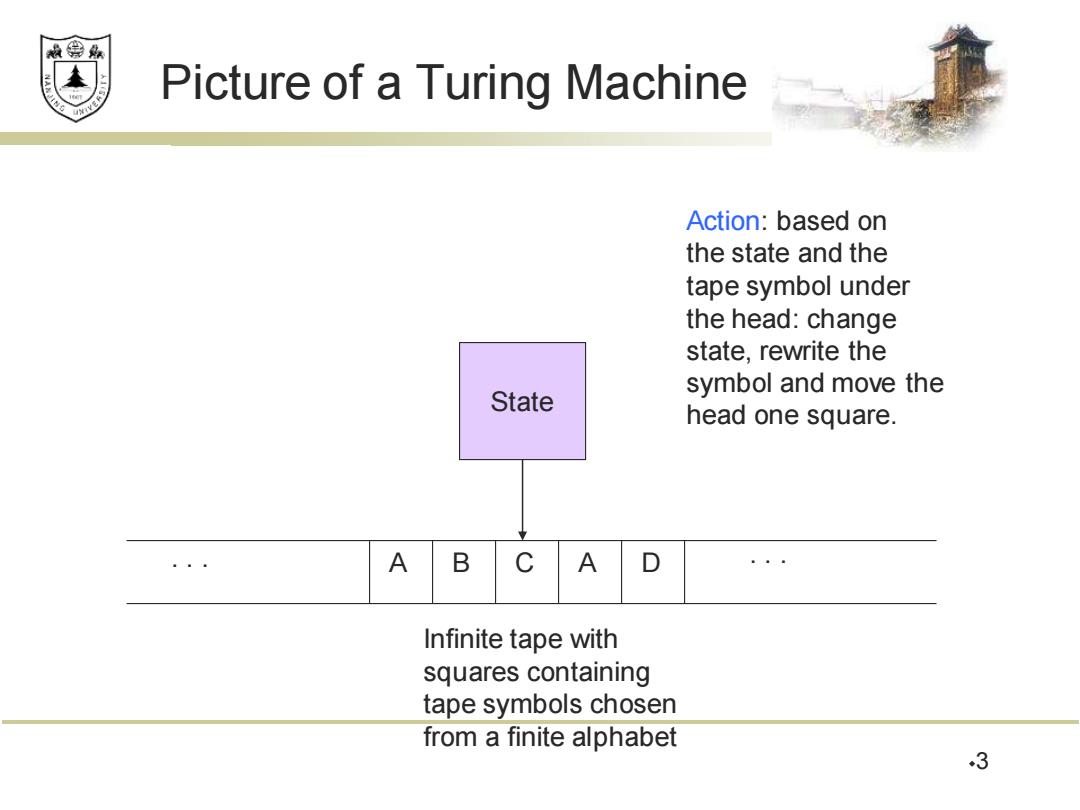
效绵 Picture of a Turing Machine Action:based on the state and the tape symbol under the head:change state,rewrite the symbol and move the State head one square. A B C A D Infinite tape with squares containing tape symbols chosen from a finite alphabet 3
Picture of a Turing Machine 3 State . . . A B C A D . . . Infinite tape with squares containing tape symbols chosen from a finite alphabet Action: based on the state and the tape symbol under the head: change state, rewrite the symbol and move the head one square

效绵鼎 Why Turing Machines? Why not deal with C programs or something like that? Answer:You can,but it is easier to prove things about TM's,because they are so simple. o And yet they are as powerful as any computer. More so,in fact,since they have infinite memory. 4
Why Turing Machines? ◼ Why not deal with C programs or something like that? ◼ Answer: You can, but it is easier to prove things about TM’s, because they are so simple. And yet they are as powerful as any computer. ◼ More so, in fact, since they have infinite memory. 4

效绵鼎 Turing-Machine Formalism A TM is described by: 1.A finite set of states (Q,typically). 2.An input alphabet(Σ,typically) 3.A tape alphabet (T,typically;contains >) 4. A transition function(δ,typically)) 5. A start state (qo,in Q,typically). 6. A blank symbol(B,in「-Σ,typically). u All tape except for the input is blank initially. 7. A set of final states (F Q,typically) 5
Turing-Machine Formalism ◼ A TM is described by: 1. A finite set of states (Q, typically). 2. An input alphabet (Σ, typically). 3. A tape alphabet (Γ, typically; contains Σ). 4. A transition function (δ, typically). 5. A start state (q0 , in Q, typically). 6. A blank symbol (B, in Γ- Σ, typically). u All tape except for the input is blank initially. 7. A set of final states (F ⊆ Q, typically). 5

效绵鼎 Conventions ■ a,b,..are input symbols. ...,X,Y,Z are tape symbols ...w,X,y,z are strings of input symbols. ,阝,.are strings of tape symbols. .6
Conventions ◼ a, b, … are input symbols. ◼ …, X, Y, Z are tape symbols. ◼ …, w, x, y, z are strings of input symbols. ◼ , ,… are strings of tape symbols. 6

效绵鼎 The Transition Function Takes two arguments: 1.A state,in Q. 2.A tape symbol in r. 6(q,Z)is either undefined or a triple of the form (P,Y,D): p is a state. Y is the new tape symbol. D is a direction,L or R. 7
The Transition Function ◼ Takes two arguments: 1. A state, in Q. 2. A tape symbol in Γ. ◼ δ(q, Z) is either undefined or a triple of the form (p, Y, D). p is a state. Y is the new tape symbol. D is a direction, L or R. 7

效绵鼎 Example:Turing Machine This TM scans its input right,looking for a 1. If it finds one,it changes it to a 0,goes to final state f,and halts. ■ If it reaches a blank,it changes it to a 1 and moves left. 8
Example: Turing Machine ◼ This TM scans its input right, looking for a 1. ◼ If it finds one, it changes it to a 0, goes to final state f, and halts. ◼ If it reaches a blank, it changes it to a 1 and moves left. 8

效绵鼎 Example:Turing Machine-(2) States ={q (start),f(final)}. Input symbols =(0,1). Tape symbols ={0,1,B). ■6(q,0)=(q,0,R) δ(q,1)=(E,0,R) ■δ(q,B)=(q,1,L) 9
Example: Turing Machine – (2) ◼ States = {q (start), f (final)}. ◼ Input symbols = {0, 1}. ◼ Tape symbols = {0, 1, B}. ◼ δ(q, 0) = (q, 0, R). ◼ δ(q, 1) = (f, 0, R). ◼ δ(q, B) = (q, 1, L). 9
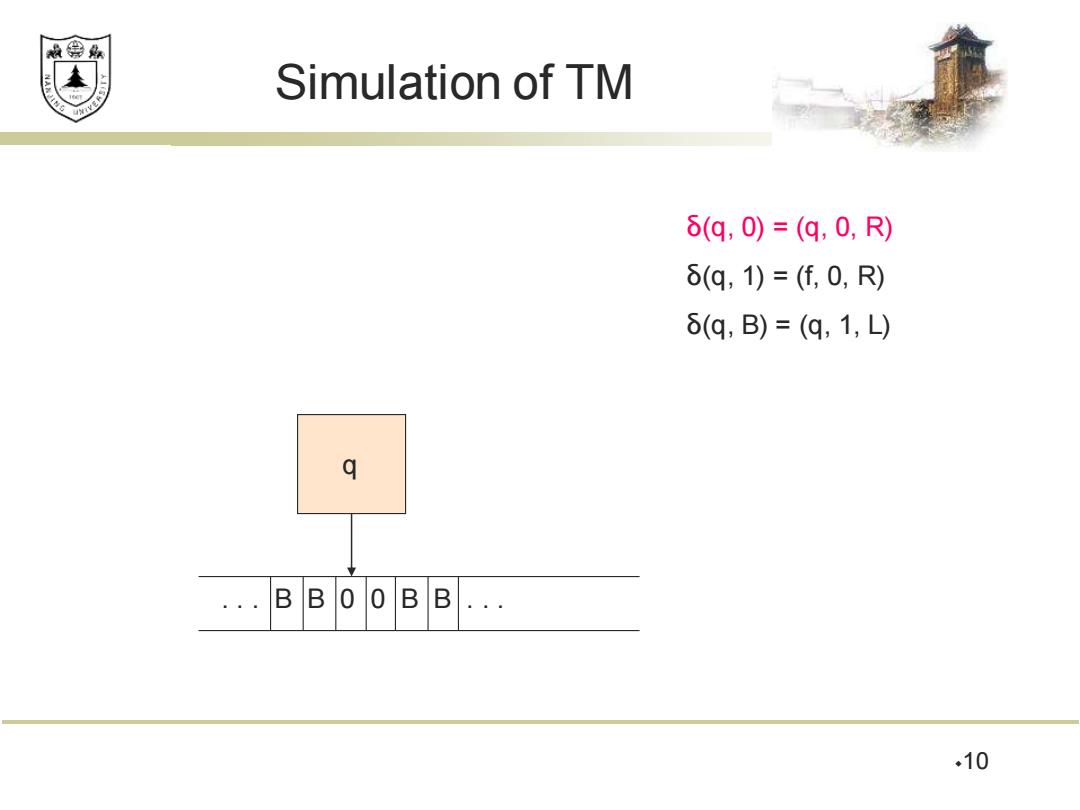
效绵鼎 Simulation of TM 6(q,0)=(q,0,R) δ(q,1)=(f,0,R) δ(q,B)=(q,1,L) q ..BB .. .10
Simulation of TM 10 δ(q, 0) = (q, 0, R) δ(q, 1) = (f, 0, R) δ(q, B) = (q, 1, L) . . . B B 0 0 B B . . . q