
实验一补充 常见空间曲线和曲面 (标准方程及Matlab作图) 1
1 实验一 补充 常见空间曲线和曲面 (标准方程及Matlab作图)

主要内容 ■球面、椭球面 ■ 单叶双曲面与双叶双曲面 ■ 椭圆抛物面与双曲抛物面 ■圆柱螺线、圆锥螺线与抛物螺线 ■Matlab绘图 2
2 主要内容 球面、椭球面 单叶双曲面与双叶双曲面 椭圆抛物面与双曲抛物面 圆柱螺线、圆锥螺线与抛物螺线 Matlab 绘图

球面 ●球面标准方程(以原点为球心) x2+y2+z2=R2 (R>0) 经度 x=R·sinp·cos8 y=R·sinp·sing 0≤0<2π =R.coso 0≤p≤π 纬度 3
3 球面 球面标准方程(以原点为球心) 2 22 2 xyz R ++= ( ) R > 0 sin cos sin sin cos x R y R z R =⋅ ⋅ =⋅ ⋅ = ⋅ ϕ θ ϕ θ ϕ 0 2 0 ≤ < ≤ ≤ θ π ϕ π 经度 纬度

椭球面 ●椭球面标准方程 ce, 1 (a,b,c>0) x=a·sinp·cos8 0≤0<2π y=b·sinp·sin0 0≤p≤π z=C·C0S0 4
4 椭球面 2 22 2 22 1 xyz abc ++= (,, ) abc > 0 sin cos sin sin cos x a y b z c ϕ θ ϕ θ ϕ =⋅ ⋅ =⋅ ⋅ = ⋅ 0 2 0 θ π ϕ π ≤ < ≤ ≤ 椭球面标准方程

单叶双曲面 ● 单叶双曲面标准方程 z2 =1 (a,b,c>0) x=M·SecΦ.cosθ 0≤0<2π y=b.secp·sin8 -π/2<0<π/2 3=c.tano 5
5 单叶双曲面 2 22 2 22 1 xyz abc +−= (,, ) abc > 0 sec cos sec sin tan x a y b z c ϕ θ ϕ θ ϕ =⋅ ⋅ =⋅ ⋅ = ⋅ 0 2 /2 /2 θ π π ϕπ ≤ < − << 单叶双曲面标准方程

双叶双曲面 ●双叶双曲面标准方程 x2 =-1 (a,b,c>0) mm x=a·tanp·cosθ 0≤0<π y=b.tanp·sin& 13 0<p<2π,9≠ Z=c·Secp 2T2 6
6 双叶双曲面 2 22 2 22 1 xyz abc + − =− ( , , 0) abc > tan cos tan sin sec x a y b z c ϕ θ ϕ θ ϕ =⋅ ⋅ =⋅ ⋅ = ⋅ 双叶双曲面标准方程 0 1 3 0 2 , , 2 2 θ π ϕ πϕ π π ≤ < << ≠

椭圆抛物面 ●椭圆抛物面标准方程 2 622 (a,b>0) x=r·a·c0s0 0≤00 z=2/2 7
7 椭圆抛物面 2 2 2 2 2 x y z a b + = ( , 0) a b > 椭圆抛物面标准方程 2 cos sin 2 x ra y rb z r θ θ =⋅⋅ =⋅⋅ = 0 2 r 0 ≤
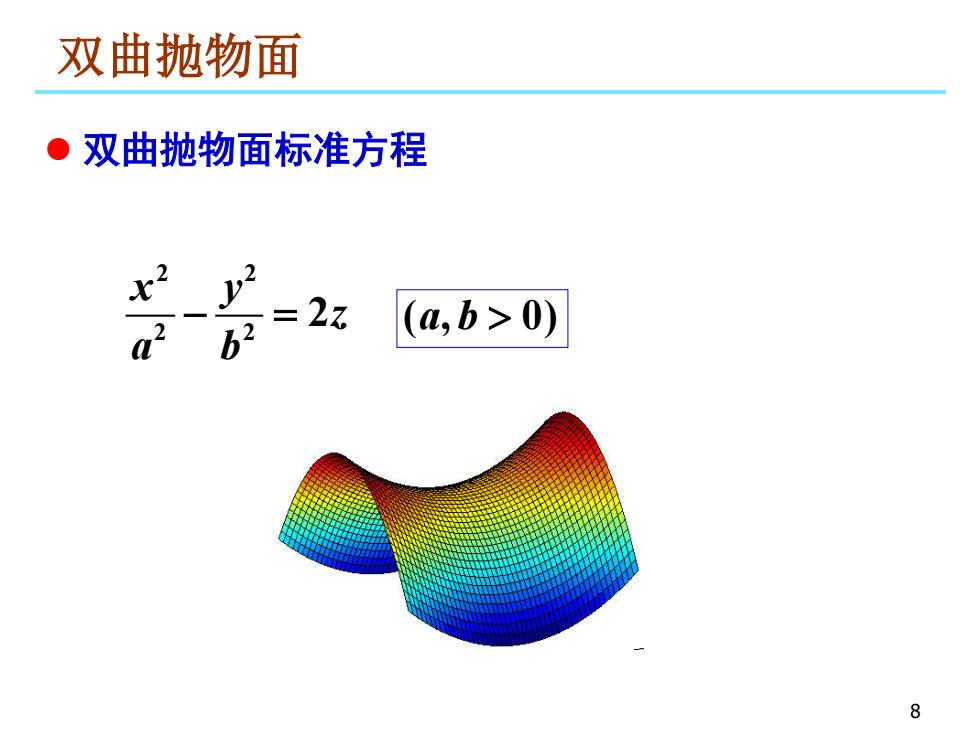
双曲抛物面 ·双曲抛物面标准方程 x2 a22 =2z (a,b>0) 8
8 双曲抛物面 2 2 2 2 2 x y z a b − = ( , 0) a b > 双曲抛物面标准方程
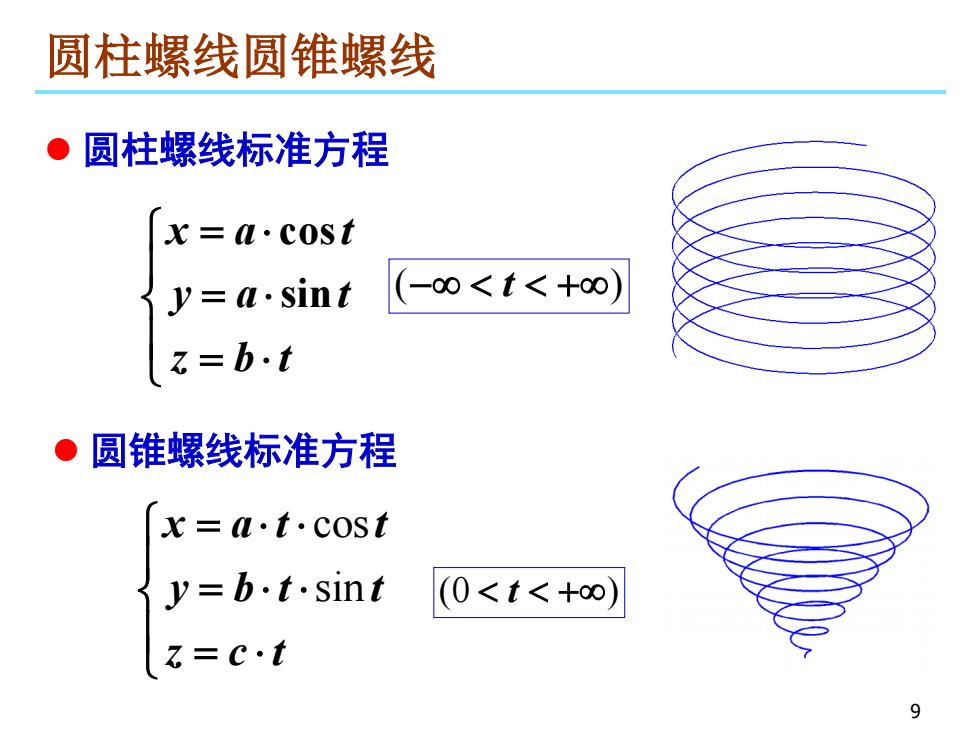
圆柱螺线圆锥螺线 ●圆柱螺线标准方程 x=u·C0st y=a.sint (-0<t<+0 z=b.t ·圆锥螺线标准方程 x=a·t.cost y=b.t.sint (0<t<+o) t=c.t 9
9 圆柱螺线圆锥螺线 cos sin xa t ya t z bt = ⋅ = ⋅ = ⋅ ( ) −∞ < < +∞ t 圆锥螺线标准方程 cos sin x at t y bt t z ct = ⋅⋅ = ⋅⋅ = ⋅ (0 ) < < +∞ t 圆柱螺线标准方程

抛物螺线 轴截面的曲边为一条抛物线的螺线 x=a·t.cost y=b.t.sint 0<t<+0 z=c…t 易知该螺线位于下面的抛物面上 y B2 10
10 抛物螺线 2 cos sin x at t y bt t z ct = ⋅⋅ = ⋅⋅ = ⋅ 0 < < +∞ t 2 2 2 2 xyz abc + = 易知该螺线位于下面的抛物面上 轴截面的曲边为一条抛物线的螺线