
MATLAB小结 第一讲、Matlab矩阵运算 1.1 Matlab基础 1.2矩阵运算… 1.3常用数学函数 第二讲、Matab绘图 2.1平面曲线 2.2空间曲线 2.3空间曲面 9 24符号绘图 0 第三讲、符号运算 11 3.1符号运算基础 3.2常见符号运算. 第四讲、编程基础 .12 4.1M文件 12 42关系运算与逻辑坛销 15 43输入输出 12 4.4选择与循环..… .13 42函数文件 13
i MATLAB 小结 第一讲、Matlab 矩阵运算 ......................................................................................................1 1.1 Matlab 基础 ................................................................................................................1 1.2 矩阵运算.....................................................................................................................3 1.3 常用数学函数.............................................................................................................5 第二讲、Matlab 绘图 ..............................................................................................................8 2.1 平面曲线.....................................................................................................................8 2.2 空间曲线.....................................................................................................................9 2.3 空间曲面.....................................................................................................................9 2.4 符号绘图.....................................................................................................................9 第三讲、符号运算.................................................................................................................11 3.1 符号运算基础...........................................................................................................11 3.2 常见符号运算...........................................................................................................11 第四讲、编程基础.................................................................................................................12 4.1 M 文件......................................................................................................................12 4.2 关系运算与逻辑运算..............................................................................................12 4.3 输入输出..................................................................................................................12 4.4 选择与循环..............................................................................................................13 4.2 函数文件..................................................................................................................13

第零讲、MATLAB介绍 MATLAB是MATrix LABoratory的缩写,是由美国Math Works公司出品的商业数学软 件。MATLAB是一种高级计算语言和交互式环境,并带有为数众多的工具箱(Toolbox), 分别适合不同领域的应用。除了数值计算、符号计算和系统仿真等主要功能外,MATLAB 还可以与其它语言(如C,C+,FORTRAN等)进行混合编程。 1970年代末到80年代初.时任美国新思西哥大学教授的Cleve m0ler(克里夫莫勒尔 为了让学生更方便地使用LINPACK及EISPACK(需要通过FORTRAN编程来实现,但当 时学生们并无相关知识),利用业余时间编了写EISPACK和LINPACK的接口程月 并取 为MATLAB,即矩阵matrix)和实验室(labotatory)两个英文单词的前三个字母的组合。这个 版本的MATLAB只能进行简单的矩阵运算,例如矩阵转置、计算行列式和特征值等。在之 后的数年里,MATLAB在多所大学里作为教学铺助软件使用,并作为面向大众的免费软件 一为清传 1983年春天,Cl ve Moler到Standford大学讲学。工程师Jack Little对MATLAB产生 了很大的兴趣。他敏锐地觉察到了MATLAB在工程领域的广阔应用前景。同年,他和CIvc Moler,Steve Bangert一起,用C语言开发了第二代MATLAB,并于1984年合作成立了 MathWorks公司,正式把MATLAB推向市场。 MATLAB最初是由Moler用FORTRAN编写的,Little和Bangert花了约一年半的时 用C重新编写了MATLAB,并增加了一些新功能,同时,Lie还 开发了第一个系统控制 具箱 ,其 一些代码到现在仍然在使用。MATLAB1.0在拉斯维加斯举行的IEEE决策与 制会议(EEE Conference on Decision and Control)上正式推出,它的第一份订单只售出了 10份拷贝。而根据MathWorks自己的数据,目前(2014年)全球有超过5000家的大专院 校采用Math Works的解决方案来开展多种技术学科的教学和研究工作。 第一讲、Matlab矩阵运算 1.1 Matlab基础 ●Matlab语句的一般形式 变量=表 计算表达式的值,并将结果赋给赋值号“=”左边的变量 ●Matlab命令的执行:回车 ·Matlab所有命令和内置函数都是由小写字母构成 ●Matlab变量的命名规则: ①字母开斗 ②由字母、数字和下划线组成 ③字母区分大小写: ④长度不要太长, 一般不要超过63个字符 ●常用功能链 Enter(回车) 运行命令或语句 ctrl+c 强制中止运行中的语句或程序 ESc 删除当前行的所有内容 Tab 命令补全功能 调出前面一个输入的命令或语句 Ctrl+K 删除从光标处到行尾的内容 Shift+Enter换行(不运行输入的命令或语句)
1 第零讲、MATLAB 介绍 MATLAB 是 MATrix LABoratory 的缩写,是由美国 MathWorks 公司出品的商业数学软 件。MATLAB 是一种高级计算语言和交互式环境,并带有为数众多的工具箱(Toolbox), 分别适合不同领域的应用。除了数值计算、符号计算和系统仿真等主要功能外,MATLAB 还可以与其它语言(如 C,C++,FORTRAN 等)进行混合编程。 1970 年代末到 80 年代初,时任美国新墨西哥大学教授的 Cleve Moler(克里夫·莫勒尔) 为了让学生更方便地使用 LINPACK 及 EISPACK (需要通过 FORTRAN 编程来实现,但当 时学生们并无相关知识),利用业余时间编了写 EISPACK 和 LINPACK 的接口程序,并取名 为 MATLAB,即矩阵(matrix)和实验室(labotatory)两个英文单词的前三个字母的组合。这个 版本的 MATLAB 只能进行简单的矩阵运算,例如矩阵转置、计算行列式和特征值等。在之 后的数年里,MATLAB 在多所大学里作为教学辅助软件使用,并作为面向大众的免费软件 广为流传。 1983 年春天,Cleve Moler 到 Standford 大学讲学。工程师 Jack Little 对 MATLAB 产生 了很大的兴趣。他敏锐地觉察到了 MATLAB 在工程领域的广阔应用前景。同年,他和 Cleve Moler,Steve Bangert 一起,用 C 语言开发了第二代 MATLAB,并于 1984 年合作成立了 MathWorks 公司,正式把 MATLAB 推向市场。 MATLAB 最初是由 Moler 用 FORTRAN 编写的,Little 和 Bangert 花了约一年半的时间 用 C 重新编写了 MATLAB,并增加了一些新功能,同时,Little 还开发了第一个系统控制工 具箱,其中一些代码到现在仍然在使用。MATLAB 1.0 在拉斯维加斯举行的 IEEE 决策与控 制会议(IEEE Conference on Decision and Control)上正式推出,它的第一份订单只售出了 10 份拷贝。而根据 MathWorks 自己的数据,目前(2014 年)全球有超过 5000 家的大专院 校采用 MathWorks 的解决方案来开展多种技术学科的教学和研究工作。 第一讲、Matlab 矩阵运算 1.1 Matlab 基础 ⚫ Matlab 语句的一般形式: 变量 = 表达式 计算表达式的值,并将结果赋给赋值号“=”左边的变量 ⚫ Matlab 命令的执行:回车 ⚫ Matlab 所有命令和内置函数都是由小写字母构成 ⚫ Matlab 变量的命名规则: ① 以字母开头; ② 由字母、数字和下划线组成; ③ 字母区分大小写; ④ 长度不要太长,一般不要超过 63 个字符 ⚫ 常用功能键 Enter(回车) 运行命令或语句 Ctrl+C 强制中止运行中的语句或程序 Esc 删除当前行的所有内容 Tab 命令补全功能 调出前面一个输入的命令或语句 Ctrl+K 删除从光标处到行尾的内容 Shift+Enter 换行 (不运行输入的命令或语句)
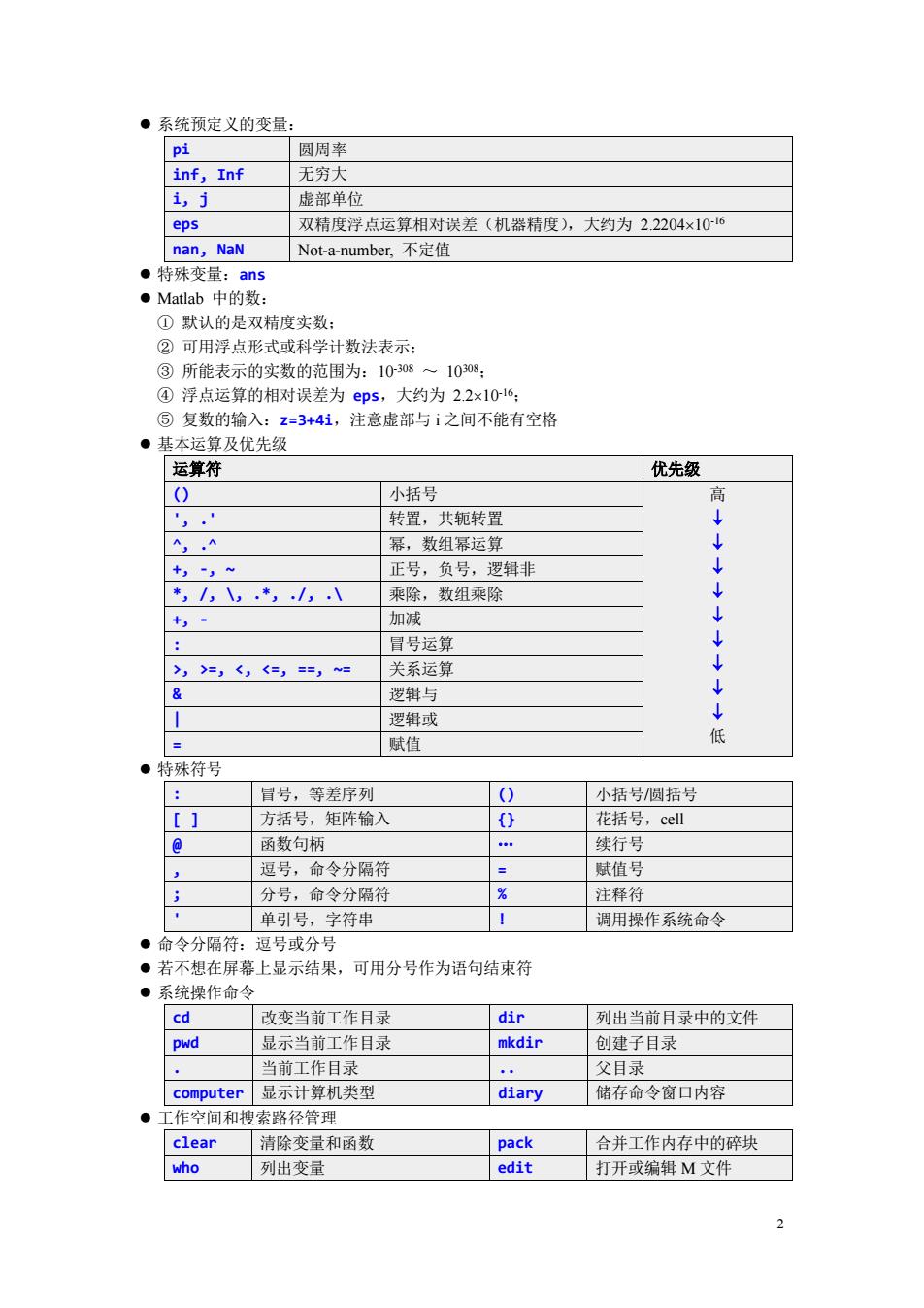
·系统预定义的变量: p 圆率 inf,Inf 无穷大 1,j 虚部单位 eps 双精度浮点运算相对误差(机器精度),大约为2.2204×1016 nan,NaN Not-a-number,.不定值 ·特殊变量 ans ●Matlab中的数: ①默认的是双精度实数 ②可用浮点形式或科学计数法表示: ③所能表示的实数的范围为:10308一100: 国复数的验入:z3+1,注意虚部与i之间不能有空格 eps 大约为2.2x1016 ●基本运算及优先级 坛算符 优先级 小括号 转置,共轭转置 AA 幂,数组幂运算 正号,负号,逻辑非 乘除,数组乘除 +, 目号运算 关系运算 逻辑与 逻辑或 赋值 低 。特殊符号 冒号,等差序列 小括号圆括号 方括号,矩阵输入 花括号,cel 函数句柄 续行号 逗号,命令分隔简 赋值号 分号,命令分隔符 图 注释符 单引号,字符串 调用操作系统命令 ●命令分隔符:逗号或分号 ·若不想在屏幕上显示结果,可用分号作为语句结束符 ●系统操作命今 cd 改变当前工作目 dir 列出当前目录中的文件 pwd 显示当前工作目录 mkdir 创建子目录 当前工作目录 父目录 computer显示计算机类型 diary 储存命令窗口内容 工作空间和搜索路径管理 clear 清除变量和函数 pack 合并工作内存中的碎块 who 列出变量 edit 打开或编辑M文件
2 ⚫ 系统预定义的变量: pi 圆周率 inf, Inf 无穷大 i, j 虚部单位 eps 双精度浮点运算相对误差(机器精度),大约为 2.220410-16 nan, NaN Not-a-number, 不定值 ⚫ 特殊变量:ans ⚫ Matlab 中的数: ① 默认的是双精度实数; ② 可用浮点形式或科学计数法表示; ③ 所能表示的实数的范围为:10-308 ~ 10308; ④ 浮点运算的相对误差为 eps,大约为 2.210-16; ⑤ 复数的输入:z=3+4i,注意虚部与 i 之间不能有空格 ⚫ 基本运算及优先级 运算符 优先级 () 小括号 高 低 ', .' 转置,共轭转置 ^, .^ 幂,数组幂运算 +, -, ~ 正号,负号,逻辑非 *, /, \, .*, ./, .\ 乘除,数组乘除 +, - 加减 : 冒号运算 >, >=, <, <=, ==, ~= 关系运算 & 逻辑与 | 逻辑或 = 赋值 ⚫ 特殊符号 : 冒号,等差序列 () 小括号/圆括号 [ ] 方括号,矩阵输入 {} 花括号,cell @ 函数句柄 … 续行号 , 逗号,命令分隔符 = 赋值号 ; 分号,命令分隔符 % 注释符 ' 单引号,字符串 ! 调用操作系统命令 ⚫ 命令分隔符:逗号或分号 ⚫ 若不想在屏幕上显示结果,可用分号作为语句结束符 ⚫ 系统操作命令 cd 改变当前工作目录 dir 列出当前目录中的文件 pwd 显示当前工作目录 mkdir 创建子目录 . 当前工作目录 .. 父目录 computer 显示计算机类型 diary 储存命令窗口内容 ⚫ 工作空间和搜索路径管理 clear 清除变量和函数 pack 合并工作内存中的碎块 who 列出变量 edit 打开或编辑 M 文件
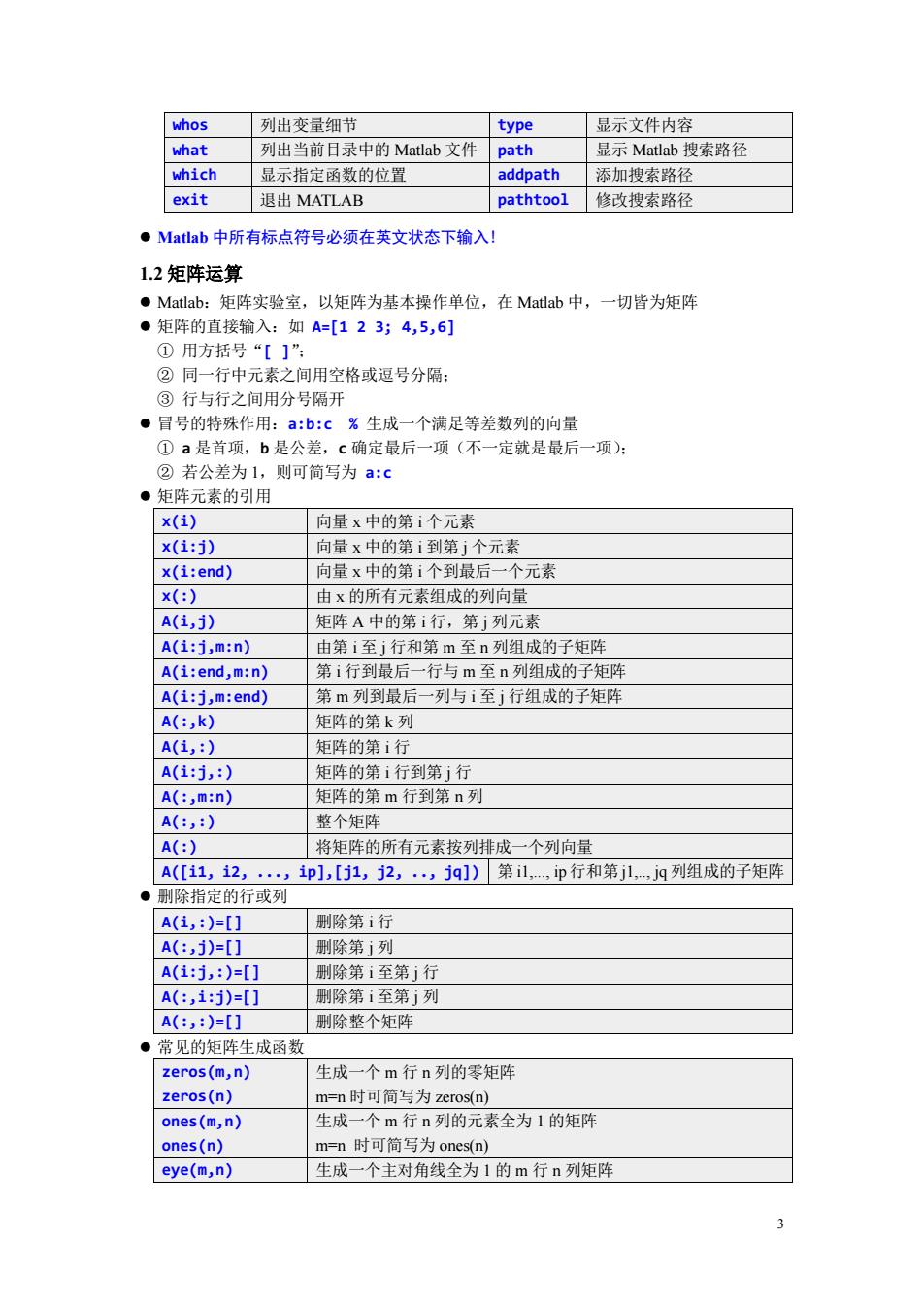
whos 列出变量细节 type 显示文件内容 what 列出当前目录中的Matlab文件 path 示Matlab搜索路名 which 显示指定函数的位置 addpath 添加搜索路径 exit 退出MATLAB pathtool 修改搜素路径 ●Matlab中所有标点符号必须在英文状态下输入! 1.2矩阵运算 ●Matlab::矩阵实验室,以矩阵为基本操作单位,在Matlab中,一切皆为矩阵 ●矩阵的直接输入:如A=[12354,5,6] ①用方括号“[]” ②同一行中元素之间用空格或逗号分隔: ③行与行之间用分号隔开 ●冒号的特殊作用:a:b:c%生成一个满足等差数列的向量 ①a是首项,b是公差,c确定晶后一项(不一定就是最后一项) ②若公差为1,则可简写为a: ●矩阵元素的引用 x(1) 向量x中的第i个元素 x(i:1) 向量x中的第1到第i个元素 x( :end) 向量x中的第1个至 个元素 由x的所有元素组成的列向量 A(i,j) 矩阵A中的第i行,第j列元素 A(i:1.m:n) 由第i至i行和第m至n列组成的子矩阵 A(i:end,m:n) 第1行到最后一行与m至n列组成的子矩阵 A(i:j,m:end) 第m列到最后一列与i至j行组成的子矩阵 A(:,k) 矩连的第k列 A(i,:) 矩阵的第;行 A(i:j,:) 矩阵的第i行到第j行 A(:,m:n) 矩阵的第m行到第n列 A(:,:) 整个矩降 A(:) 将矩阵的所有元素按列排成一个列向量 A(11,12,.,1p],[j1,j2,,j])第il,,p行和第j1jq列组成的子矩阵 除指定的行或列 A(1,:)=[] 剩除第1行 A(:,1)=1 到除第列 A(i:j,:)=[☐ 制除第1至 第j行 A(:,1:j)=[] 刷除第i至第j列 A(:,)=[ 别除整个矩阵 ·常见的矩阵生成函数 zeros(m,n) 生成 一个m行n列的零矩阵 zeros(n) m=n时可简写为zeros(n) ones(m,n)】 生成一个m行n列的元素全为1的矩阵 ones(n) m=n时可简写为ones(n) eye(m,n) 生成一个主对角线全为1的m行n列矩阵
3 whos 列出变量细节 type 显示文件内容 what 列出当前目录中的 Matlab 文件 path 显示 Matlab 搜索路径 which 显示指定函数的位置 addpath 添加搜索路径 exit 退出 MATLAB pathtool 修改搜索路径 ⚫ Matlab 中所有标点符号必须在英文状态下输入! 1.2 矩阵运算 ⚫ Matlab:矩阵实验室,以矩阵为基本操作单位,在 Matlab 中,一切皆为矩阵 ⚫ 矩阵的直接输入:如 A=[1 2 3; 4,5,6] ① 用方括号“[ ]”; ② 同一行中元素之间用空格或逗号分隔; ③ 行与行之间用分号隔开 ⚫ 冒号的特殊作用:a:b:c % 生成一个满足等差数列的向量 ① a 是首项,b 是公差,c 确定最后一项(不一定就是最后一项); ② 若公差为 1,则可简写为 a:c ⚫ 矩阵元素的引用 x(i) 向量 x 中的第 i 个元素 x(i:j) 向量 x 中的第 i 到第 j 个元素 x(i:end) 向量 x 中的第 i 个到最后一个元素 x(:) 由 x 的所有元素组成的列向量 A(i,j) 矩阵 A 中的第 i 行,第 j 列元素 A(i:j,m:n) 由第 i 至 j 行和第 m 至 n 列组成的子矩阵 A(i:end,m:n) 第 i 行到最后一行与 m 至 n 列组成的子矩阵 A(i:j,m:end) 第 m 列到最后一列与 i 至 j 行组成的子矩阵 A(:,k) 矩阵的第 k 列 A(i,:) 矩阵的第 i 行 A(i:j,:) 矩阵的第 i 行到第 j 行 A(:,m:n) 矩阵的第 m 行到第 n 列 A(:,:) 整个矩阵 A(:) 将矩阵的所有元素按列排成一个列向量 A([i1, i2, ..., ip],[j1, j2, .., jq]) 第 i1,..., ip 行和第 j1,.., jq 列组成的子矩阵 ⚫ 删除指定的行或列 A(i,:)=[] 删除第 i 行 A(:,j)=[] 删除第 j 列 A(i:j,:)=[] 删除第 i 至第 j 行 A(:,i:j)=[] 删除第 i 至第 j 列 A(:,:)=[] 删除整个矩阵 ⚫ 常见的矩阵生成函数 zeros(m,n) zeros(n) 生成一个 m 行 n 列的零矩阵 m=n 时可简写为 zeros(n) ones(m,n) ones(n) 生成一个 m 行 n 列的元素全为 1 的矩阵 m=n 时可简写为 ones(n) eye(m,n) 生成一个主对角线全为 1 的 m 行 n 列矩阵
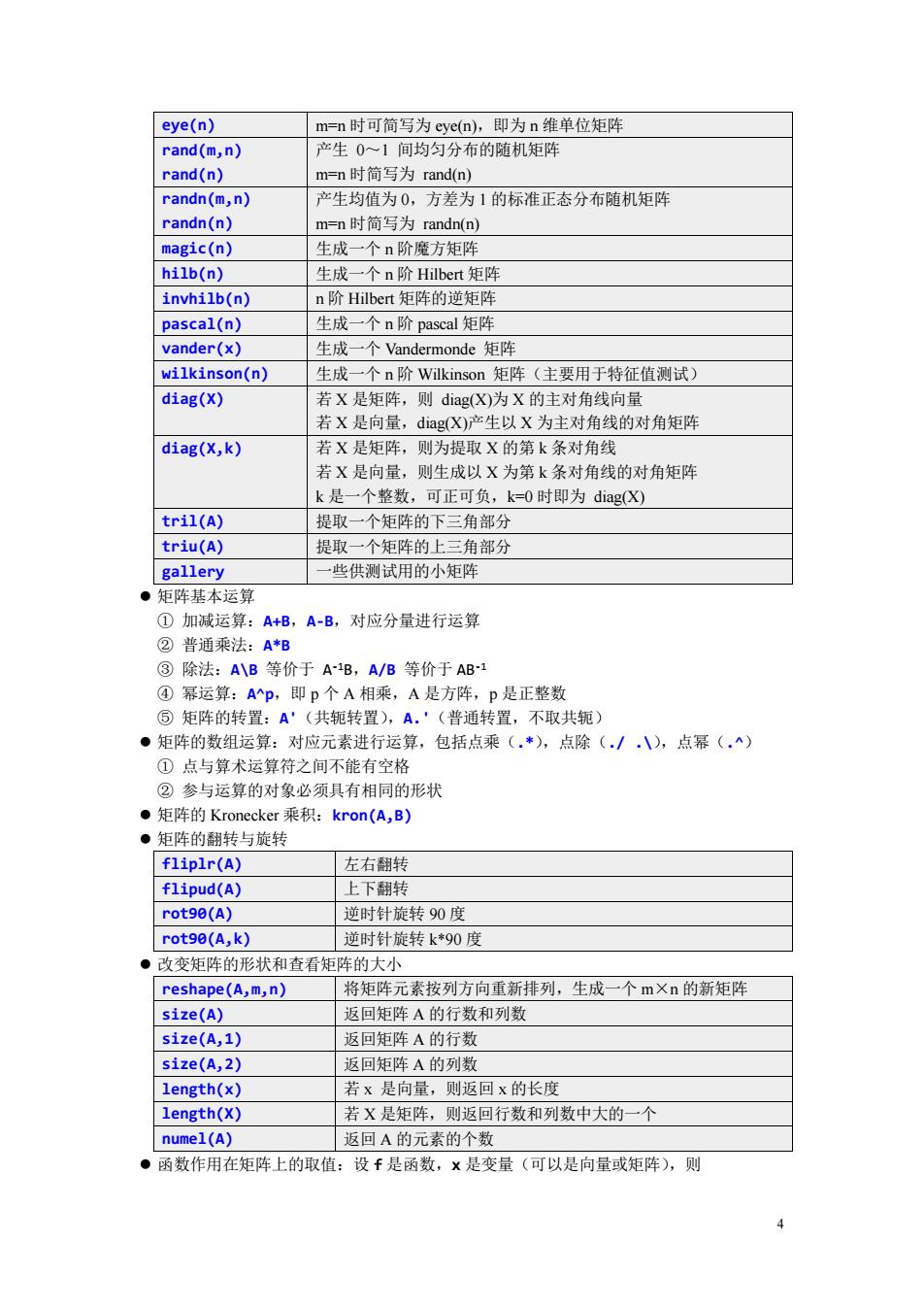
eye(n) m=n时可简写为cycn),即为n维单位矩阵 rand(m,n) 产生0~1间均匀分布的随机矩阵 rand(n) 时简写为rand(n randn(m,n) 产生均值为0,方差为1的标准正态分布随机矩阵 randn(n) m=n时简为randn(n) magic(n) 生成一个n阶魔方矩陈 hilb(n) 生成一个n阶Hilber矩 invhilb(n) n阶Hilbert矩阵的逆矩阵 pascal(n) 生成一个n阶pascal矩阵 vander(x) 生成一个Vandermonde矩阵 wilkinson(n) 生成一个n阶Wilkinson矩阵 (主要用于特征值测试) diag(X) 若X是矩阵,则diag(X)为X的主对角线向量 若X是向量,diag(X)产生以X为主对角线的对角矩阵 diag(X.k) 若X是矩阵,则为提取X的第k条对角线 若X是向量,则生成以X为第k条对角线的对角矩阵 k 个整数,可正可负,k-0时即为diag tril(A) 提取一个矩阵的下三角部分 triu(A) 提取一个矩阵的上三角部分 一些供测试用的小矩阵 矩阵基本运算 ①加减运算:A+B,A-B,对应分量进行运算 ②普通乘法:AB ③除法:AB等价于AB,A/B等价于AB1 易知辉等装P即D个A相乘,A是方阵,P是正静型 A(共轭转置), 普通 置 不取共轭 ●矩阵的数组运算:对应元素进行运算,包括点乘(.*),点除(./.八),点幂(.) ①点与算术运算符之间不能有空格 ②参与运算的对象必须具有相同的形状 ●矩阵的Kronecker乘积:kron(a,B) ●矩阵的翻转与旋转 fliplr(A) 左右翻转 flipud(A) 上下翻转 rot90(A) 逆时针旋转90度 rot90(A,k) 逆时针旋转k*90度 ●改变矩阵的形状和查看矩阵的大小 reshape(A,m,n) 将矩阵元素按列方向重新排列,生成一个m×n的新矩阵 size(A) 返回矩阵A的行数和列数 s1ze(A,1 返回矩阵A的行数 size(A,2) 返回矩阵A的列数 length(x) 若x是向量,则返回x的长度 length(x) 若X是矩阵,则返回行数和列数中大的一个 numel(A) 返回A的元素的个数 ●函数作用在矩阵上的取值:设f是函数,×是变量(可以是向量或矩阵),则
4 eye(n) m=n 时可简写为 eye(n),即为 n 维单位矩阵 rand(m,n) rand(n) 产生 0~1 间均匀分布的随机矩阵 m=n 时简写为 rand(n) randn(m,n) randn(n) 产生均值为 0,方差为 1 的标准正态分布随机矩阵 m=n 时简写为 randn(n) magic(n) 生成一个 n 阶魔方矩阵 hilb(n) 生成一个 n 阶 Hilbert 矩阵 invhilb(n) n 阶 Hilbert 矩阵的逆矩阵 pascal(n) 生成一个 n 阶 pascal 矩阵 vander(x) 生成一个 Vandermonde 矩阵 wilkinson(n) 生成一个 n 阶 Wilkinson 矩阵(主要用于特征值测试) diag(X) 若 X 是矩阵,则 diag(X)为 X 的主对角线向量 若 X 是向量,diag(X)产生以 X 为主对角线的对角矩阵 diag(X,k) 若 X 是矩阵,则为提取 X 的第 k 条对角线 若 X 是向量,则生成以 X 为第 k 条对角线的对角矩阵 k 是一个整数,可正可负,k=0 时即为 diag(X) tril(A) 提取一个矩阵的下三角部分 triu(A) 提取一个矩阵的上三角部分 gallery 一些供测试用的小矩阵 ⚫ 矩阵基本运算 ① 加减运算:A+B,A-B,对应分量进行运算 ② 普通乘法:A*B ③ 除法:A\B 等价于 A -1B,A/B 等价于 AB-1 ④ 幂运算:A^p,即 p 个 A 相乘,A 是方阵,p 是正整数 ⑤ 矩阵的转置:A'(共轭转置),A.'(普通转置,不取共轭) ⚫ 矩阵的数组运算:对应元素进行运算,包括点乘(.*),点除(./ .\),点幂(.^) ① 点与算术运算符之间不能有空格 ② 参与运算的对象必须具有相同的形状 ⚫ 矩阵的 Kronecker 乘积:kron(A,B) ⚫ 矩阵的翻转与旋转 fliplr(A) 左右翻转 flipud(A) 上下翻转 rot90(A) 逆时针旋转 90 度 rot90(A,k) 逆时针旋转 k*90 度 ⚫ 改变矩阵的形状和查看矩阵的大小 reshape(A,m,n) 将矩阵元素按列方向重新排列,生成一个 m×n 的新矩阵 size(A) 返回矩阵 A 的行数和列数 size(A,1) 返回矩阵 A 的行数 size(A,2) 返回矩阵 A 的列数 length(x) 若 x 是向量,则返回 x 的长度 length(X) 若 X 是矩阵,则返回行数和列数中大的一个 numel(A) 返回 A 的元素的个数 ⚫ 函数作用在矩阵上的取值:设 f 是函数,x 是变量(可以是向量或矩阵),则

①f(x)是作用在x的每个分量上: ②若×是矩阵,则f(x)是一个与×同形状的矩阵 ·矩阵与数的运算 ①加诚:矩阵的每个元素都与数作加减运算: ②矩阵乘以一个数:矩阵的每个元素都与数作乘法运算: ③矩阵除以一个数:每个元素都除以这个数: ④数与矩阵的点幂运算:采用数组运算,如2.^[1,2,354,5,6] 。变量的输出格式:format ①在屏幕上输出运算结果时, 可以通过format命令指定输出格式: ②foat只改变输出格式,不会改变变量的值: format short 短格式(缺省格式),小数点后4位 format long 长格式,双精度输出小数点后15位,单精度数为7位 format shortE 短E格式(科学计数格式) format longE 长E格式 format shortG 短G格式 format longG 长G格式 format rat 分数形式 format compact 紧凑格式 format loose 密松热式 format hex 十六进制格式 format bank 银行格式 format+ 分别用+,和空格表示正数,负数和零 ●变量的存储和读取 save 将所有变量保存到文件matlab.mat中 save fname 将所有变量保存到文件fname.mat中,文件扩展名可以省略 save fname.mat save fname变量列表 将指定亦品架存立件fname mat中, 存储多个变量时,变量之间用空格隔开 load fname 读取namc.mat中的所有变量 load fname变量列表从fhame,mat中读取指定的变量 ●寻找帮助 help 显示指定命令的简短使用说明 doc 以网页形式显示完整的使用帮國 lookfor 根据指定的关键词查询与之相关的命令 ●几个小转巧 ①Matlab的命令记忆功能:上下箭头键,可以先输入命令的前几个字符,再按上下键缩 小搜索范围 ②命令补全功能:Tab键 ③Esc键:删除当前命令行的所有内容 ④两个清屏命令:home、clc 1.3常用数学函数 ●三角函数 5
5 ① f(x)是作用在 x 的每个分量上; ② 若 x 是矩阵,则 f(x)是一个与 x 同形状的矩阵 ⚫ 矩阵与数的运算 ① 加减:矩阵的每个元素都与数作加减运算; ② 矩阵乘以一个数:矩阵的每个元素都与数作乘法运算; ③ 矩阵除以一个数:每个元素都除以这个数; ④ 数与矩阵的点幂运算:采用数组运算,如 2.^[1,2,3;4,5,6] ⚫ 变量的输出格式:format ① 在屏幕上输出运算结果时,可以通过 format 命令指定输出格式; ② format 只改变输出格式,不会改变变量的值; format short 短格式(缺省格式),小数点后 4 位 format long 长格式,双精度输出小数点后 15 位,单精度数为 7 位 format shortE 短 E 格式(科学计数格式) format longE 长 E 格式 format shortG 短 G 格式 format longG 长 G 格式 format rat 分数形式 format compact 紧凑格式 format loose 宽松格式 format hex 十六进制格式 format bank 银行格式 format + 分别用 +,-和空格表示正数,负数和零 ⚫ 变量的存储和读取 save 将所有变量保存到文件 matlab.mat 中 save fname save fname.mat 将所有变量保存到文件 fname.mat 中,文件扩展名可以省略 save fname 变量列表 将指定变量保存到文件 fname.mat 中, 存储多个变量时,变量之间用空格隔开 load fname 读取 fname.mat 中的所有变量 load fname 变量列表 从 fname.mat 中读取指定的变量 ⚫ 寻找帮助 help 显示指定命令的简短使用说明 doc 以网页形式显示完整的使用帮助 lookfor 根据指定的关键词查询与之相关的命令 ⚫ 几个小技巧 ① Matlab 的命令记忆功能:上下箭头键,可以先输入命令的前几个字符,再按上下键缩 小搜索范围 ② 命令补全功能: Tab 键; ③ Esc 键:删除当前命令行的所有内容 ④ 两个清屏命令:home、clc 1.3 常用数学函数 ⚫ 三角函数

sin 正2弦 sec 下划 tanh 双曲正切 反正 反正割 atanh 反双曲正切 cos 余 余割 coth 双曲余切 acos 反余弦 acsc 反余割 acoth 反双曲余切 tan sinh 双曲下 sech 型曲下划 atan 反正切 反双曲正弦 asech 反双曲正割 cot 余切 cosh 双曲余弦 csch 双曲余割 acot 反余切 acosh 反双曲余弦acsch 反双曲余割 ●指数函数 exp(x) 指数函数 log(x) 自然对数(以e为底 sqrt(x) 平方根 log2(x) 以2为底的对数 nthroot(x) n次方根 1og10(x) 常用对数(以10为底) power(x,y) 幂函数 DoW2(x) 复数运算函数 abs(x) 绝对值或模 conj(z) 取复数共轭 real(z) 取复数实部 angle(z) 相角 imag(z' 取复数虚部 complex(x,y)用实部和虚部构成复数 取整与求 ceil(x) 朝正无穷大方向取整 mod(m,n) 模数求余 fix(x) 朝0方向取整 rem(m,n) 求余数 floor(x) 朝负无穷大方向取整 sign(x) 符号函数 round(x) 四舍五入取整 gcd(m,n) 最大公约数 factor(n) 分解成素数的乘和 1cm(m,n) 最小公倍数 factorial(n)阶乘 primes(n) 不超过n的所有素数 ●数据分析 sum(x) 求和 sort(】 排序 max(x) 最大值 sortrows(X) 按行排序 min(x) 最小值 hist(x) 统计频数直方图 mean(x) 平均值 histc(x) 直方图统计 median((】个 中值 std(x) 标准差 prod(x) 元素乘积 var(x) 求方差 intmin 能表示的最小整数 realmin 能表示的最小实数 intmax 能表示的最大整数 realmax 能表示的最大实数 ●矩阵分 det 行列式 1u LU分解 inv 矩阵的逆 chol Cholesky分解 rank 矩阵的秋 QR分解 trace 矩阵的迹 schur Schur分解 norm 范数 eig 矩阵特征值和特征向玩 cond 钜阵条件数 eigs 部分特征值(稀疏矩阵) 零空间 奈异值分解 orth 值空间 svds 部分奇异 poly 特征多项式 9 广义特征值
6 sin 正弦 sec 正割 tanh 双曲正切 asin 反正弦 asec 反正割 atanh 反双曲正切 cos 余弦 csc 余割 coth 双曲余切 acos 反余弦 acsc 反余割 acoth 反双曲余切 tan 正切 sinh 双曲正弦 sech 双曲正割 atan 反正切 asinh 反双曲正弦 asech 反双曲正割 cot 余切 cosh 双曲余弦 csch 双曲余割 acot 反余切 acosh 反双曲余弦 acsch 反双曲余割 ⚫ 指数函数 exp(x) 指数函数 log(x) 自然对数(以 e 为底) sqrt(x) 平方根 log2(x) 以 2 为底的对数 nthroot(x) n 次方根 log10(x) 常用对数(以 10 为底) power(x,y) 幂函数 x y pow2(x) 2 x ⚫ 复数运算函数 abs(x) 绝对值或模 conj(z) 取复数共轭 real(z) 取复数实部 angle(z) 相角 imag(z) 取复数虚部 complex(x,y) 用实部和虚部构成复数 ⚫ 取整与求余 ceil(x) 朝正无穷大方向取整 mod(m,n) 模数求余 fix(x) 朝 0 方向取整 rem(m,n) 求余数 floor(x) 朝负无穷大方向取整 sign(x) 符号函数 round(x) 四舍五入取整 gcd(m,n) 最大公约数 factor(n) 分解成素数的乘积 lcm(m,n) 最小公倍数 factorial(n) 阶乘 primes(n) 不超过 n 的所有素数 ⚫ 数据分析 sum(x) 求和 sort(x) 排序 max(x) 最大值 sortrows(X) 按行排序 min(x) 最小值 hist(x) 统计频数直方图 mean(x) 平均值 histc(x) 直方图统计 median(x) 中值 std(x) 标准差 prod(x) 元素乘积 var(x) 求方差 intmin 能表示的最小整数 realmin 能表示的最小实数 intmax 能表示的最大整数 realmax 能表示的最大实数 ⚫ 矩阵分析 det 行列式 lu LU 分解 inv 矩阵的逆 chol Cholesky 分解 rank 矩阵的秩 qr QR 分解 trace 矩阵的迹 schur Schur 分解 norm 范数 eig 矩阵特征值和特征向量 cond 矩阵条件数 eigs 部分特征值(稀疏矩阵) null 零空间 svd 奇异值分解 orth 值空间 svds 部分奇异值 poly 特征多项式 qz 广义特征值
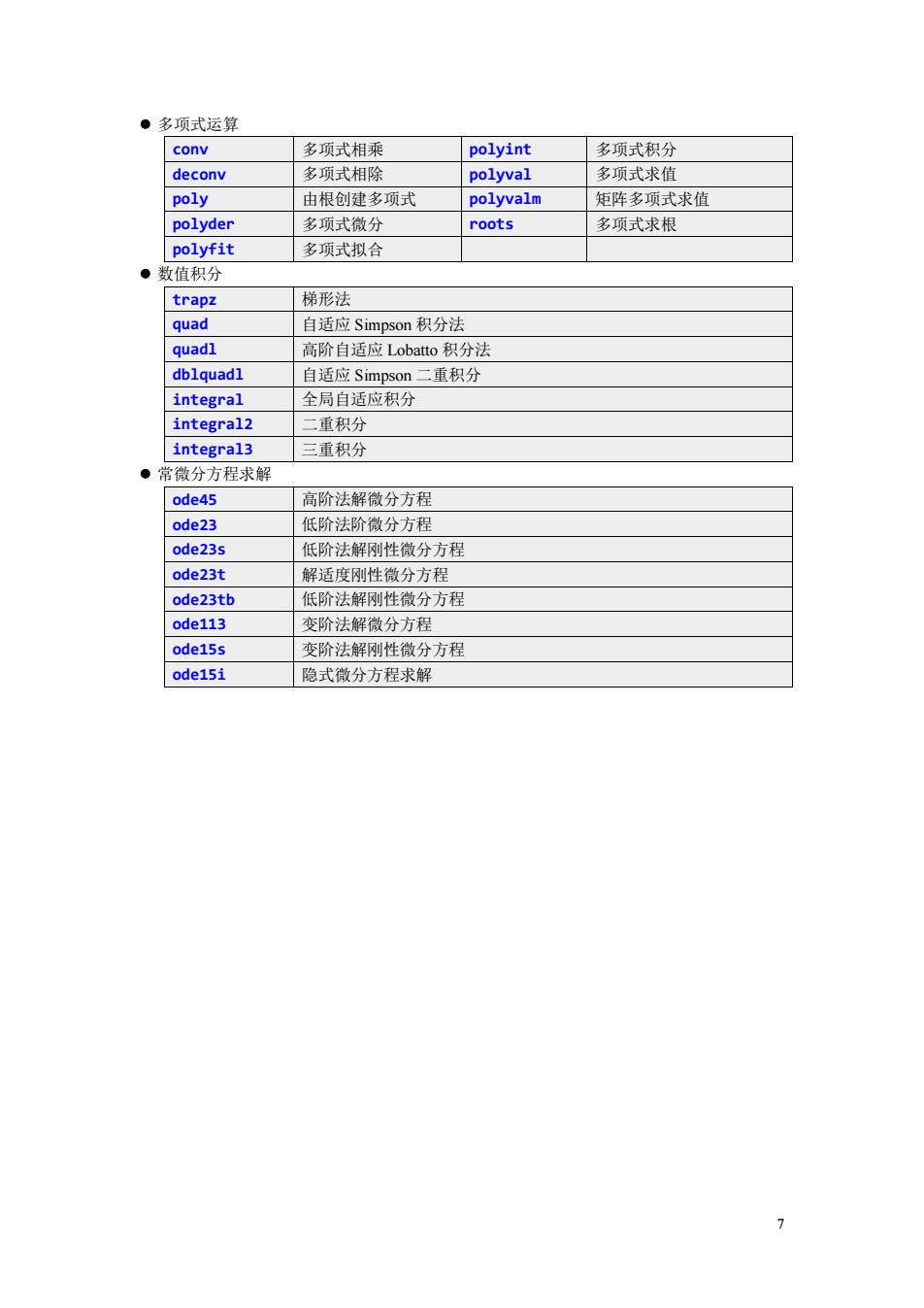
·多项式运算 conv 多面式相 polyint 多项式积分 deconv 多项式相除 polyval 多项式求 poly 由根创建多项式 polyvalm 矩阵多项式求值 polyder 多而式公 roots 多项式求根 pol fit 多项式拟合 数值积分 trapz 梯形法 quad 自话应Simpson积分法 quadl 高阶自适应Lobatto积分法 dblquad] 自适应Simpson二重积分 integral 全局自适应积分 integral2 一而和外 integral3 三重积分 常微分方程求厨 ode45 高阶法解微分方程 ode23 低阶法阶微分方程 ode23 低阶法解刚性微分方程 ode23t 解适度刚性微分方程 ode23tb 低阶法解刚性微分方程 ode113 变阶法解微分方程 ode15s 变阶法解刚性微分方程 ode15i 隐式微分方程求解
7 ⚫ 多项式运算 conv 多项式相乘 polyint 多项式积分 deconv 多项式相除 polyval 多项式求值 poly 由根创建多项式 polyvalm 矩阵多项式求值 polyder 多项式微分 roots 多项式求根 polyfit 多项式拟合 ⚫ 数值积分 trapz 梯形法 quad 自适应 Simpson 积分法 quadl 高阶自适应 Lobatto 积分法 dblquadl 自适应 Simpson 二重积分 integral 全局自适应积分 integral2 二重积分 integral3 三重积分 ⚫ 常微分方程求解 ode45 高阶法解微分方程 ode23 低阶法阶微分方程 ode23s 低阶法解刚性微分方程 ode23t 解适度刚性微分方程 ode23tb 低阶法解刚性微分方程 ode113 变阶法解微分方程 ode15s 变阶法解刚性微分方程 ode15i 隐式微分方程求解
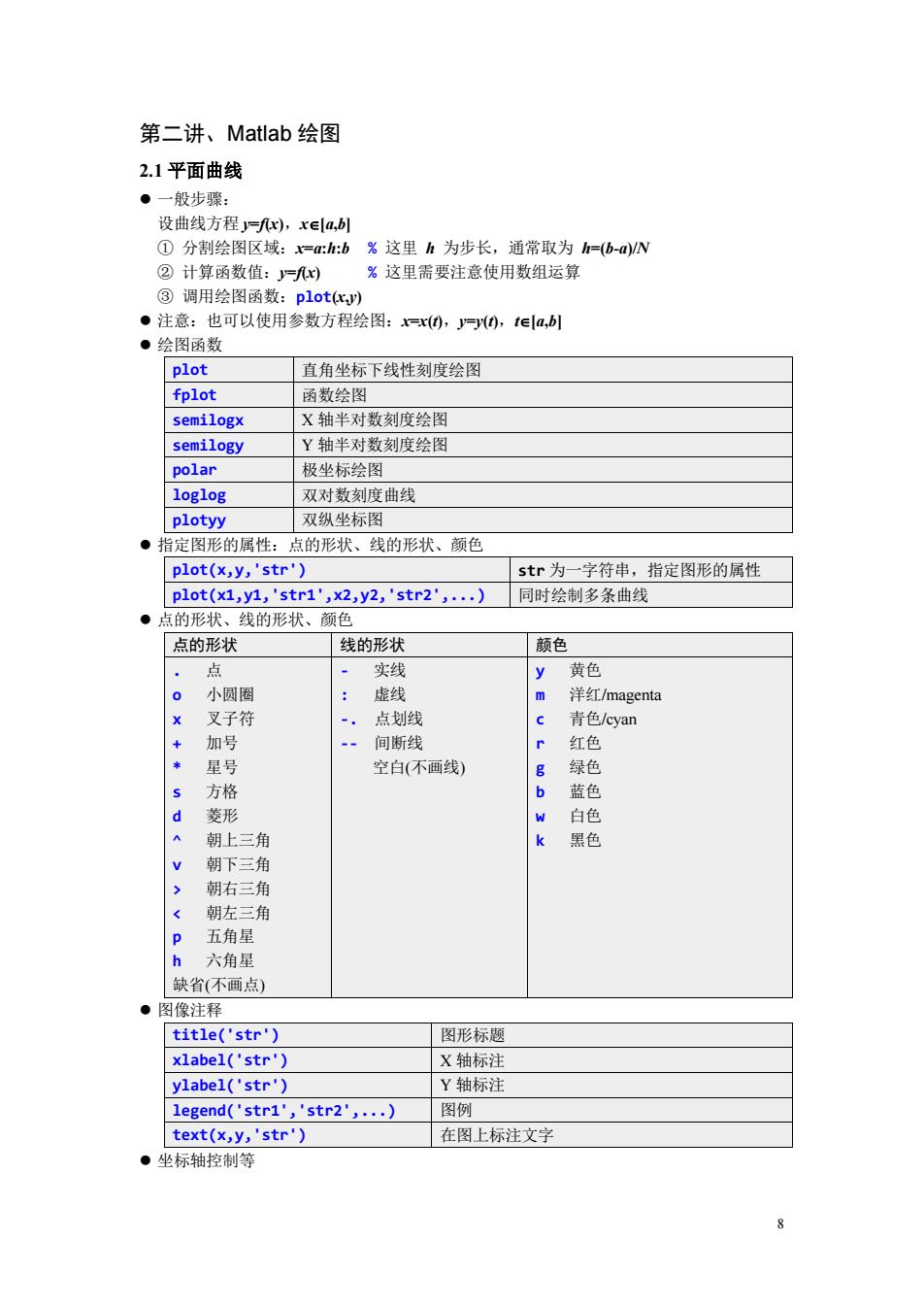
第二讲、Matlab绘图 2.1平面曲线 ·一般步骤 设曲线方程=x,xea,b1 ①分制绘图区域:=rh:b%这里h为步长,通常取为h=(b-aN @补算函数值, %这里需要注意使用数组运算 ③调用绘图函数:plot(r) ·注意:也可以使用参数方程绘图:x0,阿0,ta,b ·绘图函数 plot 直角坐标下线性刻度绘图 fplot 函数绘图 semilogx X轴半对数刻度绘图 semilogy Y轴半对数刻度绘图 polar 极坐标绘图 loglog 双对数刻度曲线 plotyy 双纵坐标图 ·指定图形的属性:点的形状、线的形状、颜色 plot(x.y.'str') str为一字符串,指定图形的属性 plot(xl,y1,'str1 ,2,y2,'str2',…)同时绘制多条曲线 点的形状、线的形状、颜色 点的形状 线的形状 颠色 点 实线 y黄色 小圆 虚线 义于行 点划 青色/cyan 加号 --间断线 红色 星号 空白(不画线) 绿色 方格 蓝色 形 朝上 三角 朝下三角 朝右三角 朝左三角 五角星 六角 省(不画点) ●图像注释 title('str') 网形标顺 xlabel('str' X轴标注 ylabel('str) Y轴标注 legend('str1','str2',...) 图例 text(x,y,'str') 在图上标注文字 坐标轴控制等
8 第二讲、Matlab 绘图 2.1 平面曲线 ⚫ 一般步骤: 设曲线方程 y=f(x),x[a,b] ① 分割绘图区域:x=a:h:b % 这里 h 为步长,通常取为 h=(b-a)/N ② 计算函数值:y=f(x) % 这里需要注意使用数组运算 ③ 调用绘图函数:plot(x,y) ⚫ 注意:也可以使用参数方程绘图:x=x(t),y=y(t),t[a,b] ⚫ 绘图函数 plot 直角坐标下线性刻度绘图 fplot 函数绘图 semilogx X 轴半对数刻度绘图 semilogy Y 轴半对数刻度绘图 polar 极坐标绘图 loglog 双对数刻度曲线 plotyy 双纵坐标图 ⚫ 指定图形的属性:点的形状、线的形状、颜色 plot(x,y,'str') str 为一字符串,指定图形的属性 plot(x1,y1,'str1',x2,y2,'str2',...) 同时绘制多条曲线 ⚫ 点的形状、线的形状、颜色 点的形状 线的形状 颜色 . 点 o 小圆圈 x 叉子符 + 加号 * 星号 s 方格 d 菱形 ^ 朝上三角 v 朝下三角 > 朝右三角 < 朝左三角 p 五角星 h 六角星 缺省(不画点) - 实线 : 虚线 -. 点划线 -- 间断线 空白(不画线) y 黄色 m 洋红/magenta c 青色/cyan r 红色 g 绿色 b 蓝色 w 白色 k 黑色 ⚫ 图像注释 title('str') 图形标题 xlabel('str') X 轴标注 ylabel('str') Y 轴标注 legend('str1','str2',...) 图例 text(x,y,'str') 在图上标注文字 ⚫ 坐标轴控制等
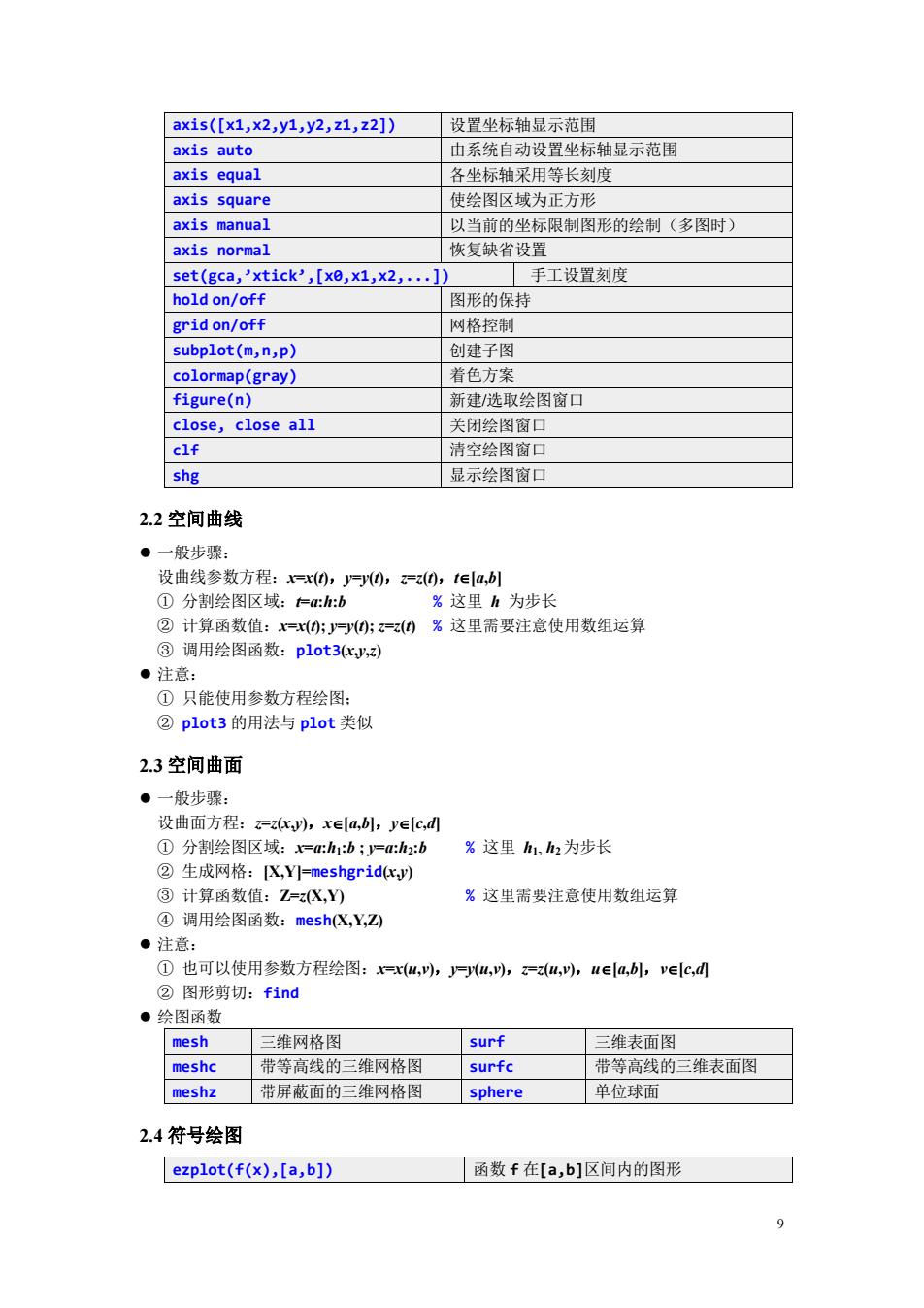
axis([x1,x2,y1,y2,z1,z2]) 设置坐标轴显示范围 axis auto 由系统自动设置坐标轴显示范围 axis equal 各坐标轴采用等长刻度 axis square 使绘图风域为正方形 axis manual 以当前的坐标阴制图形的绘生制(多图时 axis normal 恢复缺省设置 set(gca,'xtick',[x0,x1,x2,...]) 手工设置刻度 hold on/off 图形的保持 grid on/off 网格控制 subplot(m,n,p) 创建子 colormap(gray) 着色方案 figure(n) 新建/选取绘图窗口 close,close all 关闭绘图窗口 清空绘图窗可 shg 显示绘图窗口 2.2空间曲线 ·一般步骤 设曲线参数方程:x0,Jy0,2z0ta,b1 ①分割绘图区域:卡:h:b %这里h为步长 ②计算函数值:x=x0J一;0%这里需婴注意使用数组运算 ③调用绘图函数:plot3,) ·注意: ①只能使用参数方程绘图: ②plot3的用法与plot类似 2.3空间曲面 ·一般步骤: 设曲面方程:zr,y,xea,bl,yec,d ①分制绘图区域: x-a/h:b:j-a:hz:b %这里,h2为步长 ②生成网格: [X,Y]-meshgrid( ③计算函数值:Z=zX,Y) %这里需要注意使用数组运算 ④调用绘图函数:mesh(X,Y,) ·注意: ①也可以使用参数方程绘图: x,,J,吵,z,,uea,bl,vec, ②图形剪切:find 会图函数 mesh 三维网格图 surf 三维表面图 meshc 带等高线的三维网格图 surfc 带等高线的三维表面图 meshz 带屏蔽面的三维网格图 sphere 单位球面 2.4符号绘图 ezplot(f(x),[a,b]) 函数f在[a,b]区间内的图形 0
9 axis([x1,x2,y1,y2,z1,z2]) 设置坐标轴显示范围 axis auto 由系统自动设置坐标轴显示范围 axis equal 各坐标轴采用等长刻度 axis square 使绘图区域为正方形 axis manual 以当前的坐标限制图形的绘制(多图时) axis normal 恢复缺省设置 set(gca,’xtick’,[x0,x1,x2,...]) 手工设置刻度 hold on/off 图形的保持 grid on/off 网格控制 subplot(m,n,p) 创建子图 colormap(gray) 着色方案 figure(n) 新建/选取绘图窗口 close, close all 关闭绘图窗口 clf 清空绘图窗口 shg 显示绘图窗口 2.2 空间曲线 ⚫ 一般步骤: 设曲线参数方程:x=x(t),y=y(t),z=z(t),t[a,b] ① 分割绘图区域:t=a:h:b % 这里 h 为步长 ② 计算函数值:x=x(t); y=y(t); z=z(t) % 这里需要注意使用数组运算 ③ 调用绘图函数:plot3(x,y,z) ⚫ 注意: ① 只能使用参数方程绘图; ② plot3 的用法与 plot 类似 2.3 空间曲面 ⚫ 一般步骤: 设曲面方程:z=z(x,y),x[a,b],y[c,d] ① 分割绘图区域:x=a:h1:b ; y=a:h2:b % 这里 h1, h2为步长 ② 生成网格:[X,Y]=meshgrid(x,y) ③ 计算函数值:Z=z(X,Y) % 这里需要注意使用数组运算 ④ 调用绘图函数:mesh(X,Y,Z) ⚫ 注意: ① 也可以使用参数方程绘图:x=x(u,v),y=y(u,v),z=z(u,v),u[a,b],v[c,d] ② 图形剪切:find ⚫ 绘图函数 mesh 三维网格图 surf 三维表面图 meshc 带等高线的三维网格图 surfc 带等高线的三维表面图 meshz 带屏蔽面的三维网格图 sphere 单位球面 2.4 符号绘图 ezplot(f(x),[a,b]) 函数 f 在[a,b]区间内的图形