
数字图像处理 频域变换
数字图像处理 频域变换

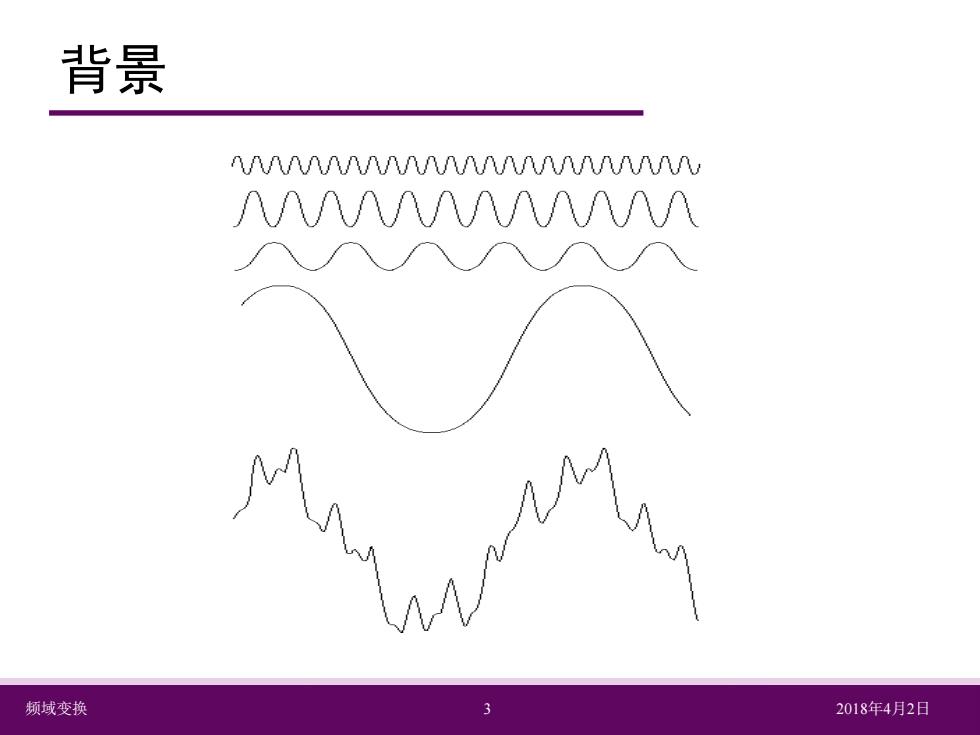
背景 ●法国数学家傅里叶(生于1768年)在1822年出版的 《热分析理论》一书中指出:任何周期函数都可 以表达为不同频率的正弦和或余弦和的形式,即 傅里叶级数。 ● 20世纪50年代后期,快速傅里叶变换算法出现, 得到了广泛的应用。 频域变换 2 2018年4月2日
频域变换 2 2018年4月2日 背景 法国数学家傅里叶(生于1768年)在1822年出版的 《热分析理论》一书中指出:任何周期函数都可 以表达为不同频率的正弦和或余弦和的形式,即 傅里叶级数。 20世纪50年代后期,快速傅里叶变换算法出现, 得到了广泛的应用
背景 MAAMA 频域变换 2018年4月2日
频域变换 3 2018年4月2日 背景

背景 ·在计算机的图像处理中,所谓图像变换就是为达 到图像处理的某种目的而使用的一种数学技巧。 图像函数经过变换后处理起来较变换前更加简单 和方便,由于这种变换是对图像函数而言的,所 以称为图像变换。 ● 现在研究的图像变换基本上都是正交变换。正交 变换可以减少图像数据的相关性,获取图像的整 体特点,有利于用较少的数据量表示原始图像, 这对图像的分析、存储以及图像的传输都是非常 有意义的。 频域变换 4 2018年4月2日
频域变换 4 2018年4月2日 背景 在计算机的图像处理中,所谓图像变换就是为达 到图像处理的某种目的而使用的一种数学技巧。 图像函数经过变换后处理起来较变换前更加简单 和方便,由于这种变换是对图像函数而言的,所 以称为图像变换。 现在研究的图像变换基本上都是正交变换。正交 变换可以减少图像数据的相关性,获取图像的整 体特点,有利于用较少的数据量表示原始图像, 这对图像的分析、存储以及图像的传输都是非常 有意义的

傅里叶变换 傅里叶基本思想: 将任意周期函数,分解为一组不同频率的正弦或者余 弦函数的加权和。 ·傅里叶变换的效果: 把函数从时间域变到频率域 ·傅里叶变换的作用: 把图像或者信号在频域中进行处理,从而达到简化处 理过程、增强处理效果。 频域变换 5 2018年4月2日
频域变换 5 2018年4月2日 傅里叶变换 傅里叶基本思想: 将任意周期函数,分解为一组不同频率的正弦或者余 弦函数的加权和。 傅里叶变换的效果: 把函数从时间域变到频率域 傅里叶变换的作用: 把图像或者信号在频域中进行处理,从而达到简化处 理过程、增强处理效果

傅里叶变换的历史 "An arbitrary function, continuous or with discontinuities,defined in a finite interval by an arbitrarily capricious graph can always be expressed as a sum of sinusoids" J.B.J.Fourier Fig.2.2 Jean B.Joseph Fourier(1768-1830) Picture from R.X.Gao and R.Yan,Wavelets:Theory and Applications for Manufacturing Chapter 2 From Fourier Transform to Wavelet Transform:A Historical Perspective DOI 10.1007/978-1-4419-1545-0 2,Springer Science+Business Media,LLC 2011 频域变换 2018年4月2日
频域变换 6 2018年4月2日 傅里叶变换的历史 Picture from R.X. Gao and R. Yan, Wavelets: Theory and Applications for Manufacturing Chapter 2 From Fourier Transform to Wavelet Transform: A Historical Perspective DOI 10.1007/978-1-4419-1545-0_2, © Springer Science+Business Media, LLC 2011

傅里叶生平 Jean-Baptiste Joseph Fourier(1768-1830) ·1768年生于法国 ● 1807年提出“任何周期 信号都可用正弦函数级 数表示” ● 1829年狄里赫利第一个 给出收敛条件 拉格朗日、拉普拉斯、 泊松反对发表 1822年首次发表在“热 的分析理论”一书中 频域变换 7 2018年4月2日
频域变换 7 2018年4月2日 傅里叶生平 Jean-Baptiste Joseph Fourier (1768-1830) 1768年生于法国 1807年提出“任何周期 信号都可用正弦函数级 数表示” 1829年狄里赫利第一个 给出收敛条件 拉格朗日、拉普拉斯、 泊松反对发表 1822年首次发表在“热 的分析理论”一书中
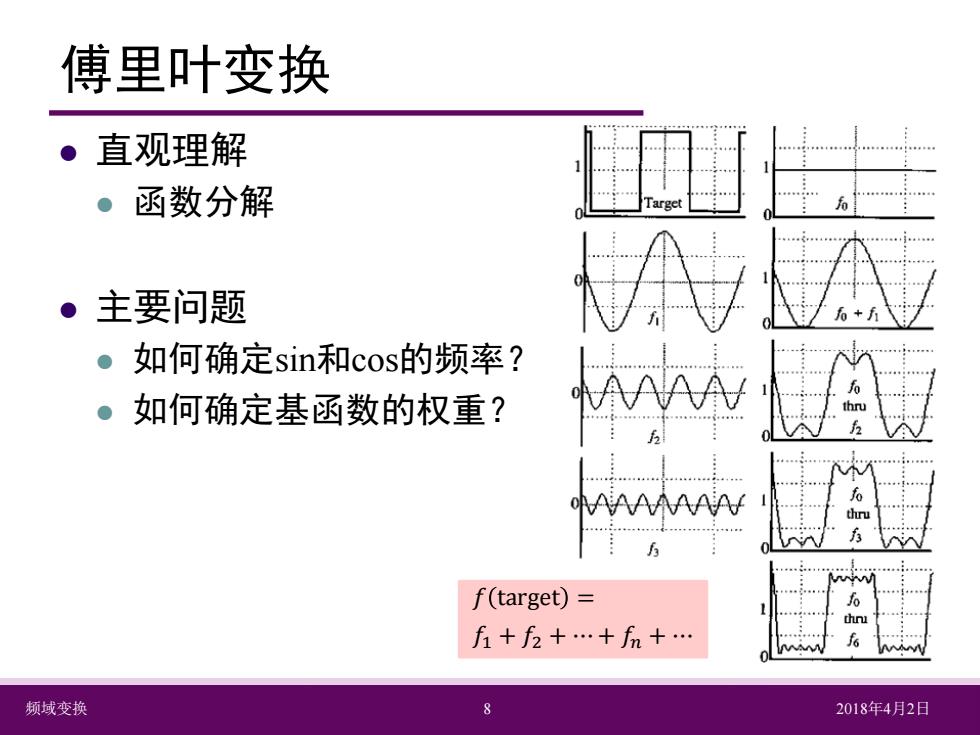
傅里叶变换 直观理解 。函数分解 主要问题 。如何确定sin和cos的频率? 。如何确定基函数的权重? AAAAAA fo thru f(target)= fi+f2+…+fn+… 频域变换 2018年4月2日
频域变换 8 2018年4月2日 傅里叶变换 直观理解 函数分解 主要问题 如何确定sin和cos的频率? 如何确定基函数的权重? 𝑓𝑓 target = 𝑓𝑓1 + 𝑓𝑓2 + ⋯ + 𝑓𝑓𝑛𝑛 + ⋯

傅里叶变换 f(x) 傅里叶变换 F(u) 令f(x)为实变量x的一维连续函数,则一维连续函数的傅 里叶变换对定义为: F[f(c】=F(u)=∫f(x)e2rurd F-IF(u)]=f()=F(u)ej2rurdu 上式中j=V一1,x为时域变量,u为频域变量。 频域变换 9 2018年4月2日
频域变换 9 2018年4月2日 傅里叶变换 令𝑓𝑓(𝑥𝑥)为实变量𝑥𝑥的一维连续函数,则一维连续函数的傅 里叶变换对定义为: 𝑓𝑓(𝑥𝑥) 傅里叶变换 𝐹𝐹(𝑢𝑢) 上式中𝑗𝑗 = −1, 𝑥𝑥为时域变量,𝑢𝑢为频域变量

傅里叶变换 ● 连续函数的傅里叶变换 ·狄利克雷条件: ·令f(x)为实变量x的一维连续函数,狄利克雷条件为f(x) 具有有限个间断点、具有有限个极值点、绝对可积。 。在实际应用中,这些条件基本上都是可以满足的。 ·存在性定理:当f(x)满足狄利克雷条件时,则对应 的傅里叶变换对一定存在。 频域变换 10 2018年4月2日
频域变换 10 2018年4月2日 傅里叶变换 连续函数的傅里叶变换 狄利克雷条件: 令𝑓𝑓(𝑥𝑥)为实变量𝑥𝑥的一维连续函数,狄利克雷条件为𝑓𝑓(𝑥𝑥) 具有有限个间断点、具有有限个极值点、绝对可积。 在实际应用中,这些条件基本上都是可以满足的。 存在性定理:当𝑓𝑓(𝑥𝑥)满足狄利克雷条件时,则对应 的傅里叶变换对一定存在