
数字图像处理 形态学及其应用
数字图像处理 形态学及其应用

数学形态学概述 ·数学形态学 。数学形态学是法国和德国的科学家在研究岩石结构 时建立的一门学科(1664)。 ·形态学的用途是获取物体拓扑和结构信息,它通过 物体和结构元素相互作用的某些运算,得到物体更 本质的形态。 ·在图像处理中的应用主要是: ·利用形态学的基本运算,对图像进行观察和处理, 从而达到改善图像质量的目的; 描述和定义图像的各种几何参数和特征,如面积、 周长、连通度、颗粒度、骨架和方向性等。 形态学及其应用 2 数字图像处理,2018年春季
形态学及其应用 2 数字图像处理· 2018年春季 数学形态学概述 数学形态学 数学形态学是法国和德国的科学家在研究岩石结构 时建立的一门学科(1664)。 形态学的用途是获取物体拓扑和结构信息,它通过 物体和结构元素相互作用的某些运算,得到物体更 本质的形态。 在图像处理中的应用主要是: 利用形态学的基本运算,对图像进行观察和处理, 从而达到改善图像质量的目的; 描述和定义图像的各种几何参数和特征,如面积、 周长、连通度、颗粒度、骨架和方向性等

数学形态学概述 ·数学形态学的数学基础和所用语言是集合论,因 此它具有完备的数学基础。这为形态学用于图像 分析和处理、形态滤波器的特性分析和系统设计 奠定了坚实的基础。 ● 数学形态学的应用可以简化图像数据,保持它们 基本的形状特性,并除去不相干的结构。 数学形态学方法利用一个称作结构元素的“探针 ”收集图像的信息。当探针在图像中不断移动时 ,便可考察图像各个部分之间的相互关系,从而 了解图像的结构特征。 形态学及其应用 数字图像处理,2018年春季
形态学及其应用 3 数字图像处理· 2018年春季 数学形态学概述 数学形态学的数学基础和所用语言是集合论,因 此它具有完备的数学基础。这为形态学用于图像 分析和处理、形态滤波器的特性分析和系统设计 奠定了坚实的基础。 数学形态学的应用可以简化图像数据,保持它们 基本的形状特性,并除去不相干的结构。 数学形态学方法利用一个称作结构元素的“探针 ”收集图像的信息。当探针在图像中不断移动时 ,便可考察图像各个部分之间的相互关系,从而 了解图像的结构特征

数学形态学概述 ●迄今为止, 还没有一种方法能像数学形态学那样 既有坚实的理论基础,简洁、朴素、统一的基本 思想,又有如此广泛的实用价值。有人称数学形 态学在理论上是严谨的,在基本观念上却是简单 和优美的。 ·数学形态学是一门建立在严格数学理论基础上的 学科,其基本思想和方法对图像处理的理论和技 术产生了重大影响。 ● 数学形态学已经构成一种新的图像处理方法和理 论,成为计算机数字图像处理的重要研究领域。 形态学及其应用 数字图像处理,2018年春季
形态学及其应用 4 数字图像处理· 2018年春季 数学形态学概述 迄今为止, 还没有一种方法能像数学形态学那样 既有坚实的理论基础,简洁、 朴素、 统一的基本 思想,又有如此广泛的实用价值。有人称数学形 态学在理论上是严谨的,在基本观念上却是简单 和优美的。 数学形态学是一门建立在严格数学理论基础上的 学科,其基本思想和方法对图像处理的理论和技 术产生了重大影响。 数学形态学已经构成一种新的图像处理方法和理 论,成为计算机数字图像处理的重要研究领域
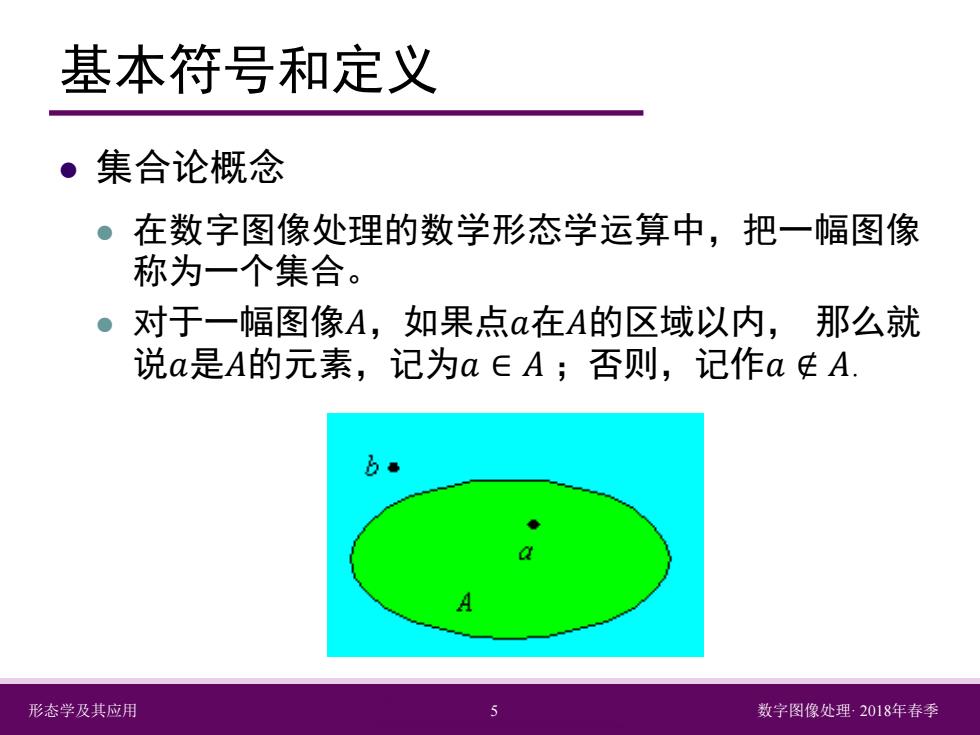
基本符号和定义 ·集合论概念 ●在数字图像处理的数学形态学运算中,把一幅图像 称为一个集合。 。对于一幅图像A,如果点a在A的区域以内,那么就 说a是A的元素,记为aEA;否则,记作aA. 形态学及其应用 数字图像处理2018年春季
形态学及其应用 5 数字图像处理· 2018年春季 基本符号和定义 集合论概念 在数字图像处理的数学形态学运算中,把一幅图像 称为一个集合。 对于一幅图像𝐴𝐴,如果点𝑎𝑎在𝐴𝐴的区域以内, 那么就 说𝑎𝑎是𝐴𝐴的元素,记为𝑎𝑎 ∈ 𝐴𝐴 ;否则,记作𝑎𝑎 ∉ 𝐴𝐴

基本符号和定义 ·B包含于A ● 设有两幅图像A和B。如果对于B中所有的元素a:, 都有a1∈A,则称B包含于A,记作BcA, 形态学及其应用 6 数字图像处理,2018年春季
形态学及其应用 6 数字图像处理· 2018年春季 基本符号和定义 𝐵𝐵包含于𝐴𝐴 设有两幅图像𝐴𝐴和𝐵𝐵。如果对于𝐵𝐵中所有的元素𝑎𝑎𝑖𝑖, 都有𝑎𝑎𝑖𝑖 ∈ 𝐴𝐴 ,则称𝐵𝐵包含于𝐴𝐴,记作𝐵𝐵 ⊂ 𝐴𝐴
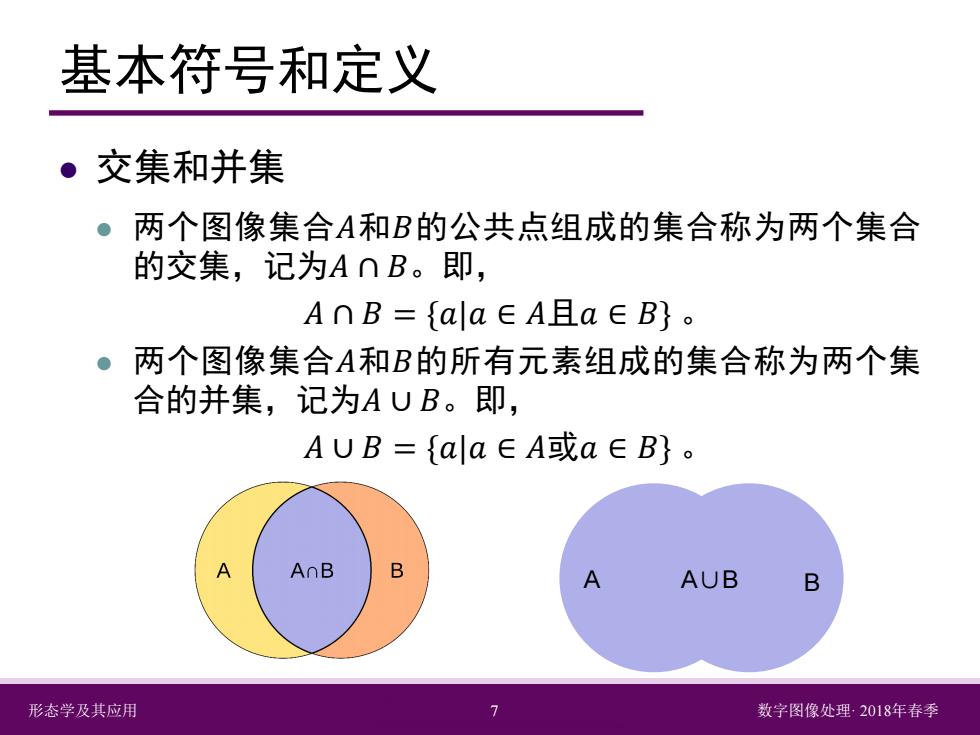
基本符号和定义 。交集和并集 ●两个图像集合A和B的公共点组成的集合称为两个集合 的交集,记为A∩B。即, AnB={aa∈A且a∈B}。 两个图像集合A和B的所有元素组成的集合称为两个集 合的并集,记为AUB。即, AUB={ala∈A或a∈B}。 AnB B A AUB B 形态学及其应用 数字图像处理2018年春季
形态学及其应用 7 数字图像处理· 2018年春季 基本符号和定义 交集和并集 两个图像集合𝐴𝐴和𝐵𝐵的公共点组成的集合称为两个集合 的交集,记为𝐴𝐴 ∩ 𝐵𝐵。即, 𝐴𝐴 ∩ 𝐵𝐵 = {𝑎𝑎|𝑎𝑎 ∈ 𝐴𝐴且𝑎𝑎 ∈ 𝐵𝐵} 。 两个图像集合𝐴𝐴和𝐵𝐵的所有元素组成的集合称为两个集 合的并集,记为𝐴𝐴 ∪ 𝐵𝐵。即, 𝐴𝐴 ∪ 𝐵𝐵 = {𝑎𝑎|𝑎𝑎 ∈ 𝐴𝐴或𝑎𝑎 ∈ 𝐵𝐵} 。 A A∪B B

基本符号和定义 ·补集 。设有一幅图像X,所有X区域以外的点构成的集合称为X 的补集,记作Xc。 。显然,如果B∩X=,则B在X的补集内。 Xc 形态学及其应用 8 数字图像处理·2018年春季
形态学及其应用 8 数字图像处理· 2018年春季 基本符号和定义 补集 设有一幅图像𝑋𝑋,所有𝑋𝑋区域以外的点构成的集合称为𝑋𝑋 的补集,记作𝑋𝑋𝑐𝑐 。 显然,如果𝐵𝐵 ∩ 𝑋𝑋 = ∅,则𝐵𝐵在𝑋𝑋的补集内。 X Xc

基本符号和定义 。击中 ●设有两幅图像B和A。若存在这样一个点,它既是B的 元素,又是A的元素,A∩B≠0则称B击中A,记作 B↑A。 B 形态学及其应用 9 数字图像处理2018年春季
形态学及其应用 9 数字图像处理· 2018年春季 基本符号和定义 击中 设有两幅图像𝐵𝐵和𝐴𝐴。若存在这样一个点,它既是𝐵𝐵的 元素,又是𝐴𝐴的元素,𝐴𝐴 ∩ 𝐵𝐵 ≠ ∅ 则称𝐵𝐵击中𝐴𝐴,记作 𝐵𝐵 ↑ 𝐴𝐴。 A B

基本符号和定义 。击不中 ●设有两幅图像B和A。若不存在任何一个点,它既是B 的元素,又是A的元素,即B和A的交集是空,则称B 不击中A,记作A∩B≠0. B 形态学及其应用 10 数字图像处理,2018年春季
形态学及其应用 10 数字图像处理· 2018年春季 基本符号和定义 击不中 设有两幅图像𝐵𝐵和𝐴𝐴。若不存在任何一个点,它既是𝐵𝐵 的元素,又是𝐴𝐴的元素,即𝐵𝐵和𝐴𝐴的交集是空,则称𝐵𝐵 不击中𝐴𝐴,记作𝐴𝐴 ∩ 𝐵𝐵 ≠ ∅. A B