
峰一缘碧棉鹅 使用教材:许力等编著,《工程化学》,兰州大学出版社 授课对象:非化学类各专业学生 主讲教师: 董文魁、许力、李静萍等
使用教材:许力等编著,《工程化学》,兰州大学出版社 授课对象:非化学类各专业学生 主讲教师:董文魁、许力、李静萍等

第五章物质结构基础 第一节氢原子结构 一、人类对原子概念的认识 J.Dalton的“原子论” W.Thomson的原子“浸入模型” E.Rutherford的原子“含核模型” E.Schrodinger的原子“波动模型
第一节 氢原子结构 一、人类对原子概念的认识 第五章 物质结构基础 J.Dalton的“原子论” E.Schrodinger的原子“波动模型” E.Rutherford的原子“含核模型” W.Thomson 的原子“浸入模型

二、氢原子光谱和玻尔理论 (1)氢原子光谱 太阳光或白炽灯发出的白光,通过玻璃三棱镜时,所含不同波长的光可 折射成红、橙、黄、绿、青、蓝、紫等没有明显分界线的光谱,这类光 谱称为连续光谱。 原子(包括氢原子)得到能量(高温、通电)会发出单色光,经过棱镜 分光得到线状光谱。即原子光谱属于不连续光谱。每种元素都有自己的 特征线状光谱。氢原子光谱如图所示。四条谱线的波长、频率的关系式 一并列出。 氢原子光谱的特征: ★不连续光谱,即线状光谱。 ★其频率具有一定的规律。 Balmer经验公式: v=3289×105(7·元)s n=3,4,5,6
二、氢原子光谱和玻尔理论 (1)氢原子光谱 太阳光或白炽灯发出的白光,通过玻璃三棱镜时,所含不同波长的光可 折射成红、橙、黄、绿、青、蓝、紫等没有明显分界线的光谱,这类光 谱称为连续光谱。 原子(包括氢原子)得到能量(高温、通电)会发出单色光,经过棱镜 分光得到线状光谱。即原子光谱属于不连续光谱。每种元素都有自己的 特征线状光谱。氢原子光谱如图所示。四条谱线的波长、频率的关系式 一并列出。 氢原子光谱的特征: ★不连续光谱,即线状光谱。 ★其频率具有一定的规律。 Balmer经验公式: n = 3,4,5,6

(2)玻尔理论 1913年丹麦物理学家Bor发表了原子结构理论的三 点假设: △核外电子只能在有确定半径和能量的轨道上运动,且不辐能量。 △通常,电子处在离核最近的轨道上,能量最低一基态;原子 得能量后,电子被激发到高能道上,原子处于激发态。 ■▲从激发态回到基态释放光能,光的频率取决于轨道间的能量差。 Yw B2-E 2-1 为
(2)玻尔理论 ◼ 1913年丹麦物理学家Bohr发表了原子结构理论 的三 点假设: ◼ ▲核外电子只能在有确定半径和能量的轨道上运动,且不辐能量。 ◼ ▲通常,电子处在离核最近的轨道上,能量最低—基态; 原子 得能量后,电子被激发到高能轨道上,原子处于激发态。 ◼ ▲从激发态回到基态释放光能,光的频率取决于轨道间的能量差

三、 微观粒子的波粒二象性 1924年,法国年轻的物理学家L.de Broglie(1892 1987)指出,对于光的本质的研究,人们长期以来注重其波动 性而忽略其粒子性;与其相反,对于实物粒子的研究中,人 们过分重视其粒子性而忽略了其波动性。 L.de Broglie从Cinstein的质能联系公式E=mc2和光子 的能量公式E=hv的联立出发,进行推理: h mc2 hv .'mc2 =h. mc 用P表示动量,则P=mc,故有公式 h
三、 微观粒子的波粒二象性 1924 年,法国年轻的物理学家 L. de Broglie ( 1892 — 1987 )指出,对于光的本质的研究,人们长期以来注重其波动 性而忽略其粒子性;与其相反,对于实物粒子的研究中,人 们过分重视其粒子性而忽略了其波动性。 L. de Broglie 从 Einstein 的质能联系公式 E = m c 2 和光子 的能量公式 E = h 的联立出发,进行推理: = = = h mc c mc h mc h 2 2 = h P 用 P 表示动量,则 P = mc ,故有公式

式子的左侧动量P是表示粒子性的物理量,而右侧波长入是 表示波动性的物理量。二者通过公式联系起来。 de Broglie认为具有动量P的微观粒子,其物质波的波长 为入, h 1927年,de Broglie的预言被电子衍射实验所证实,这种物 质波称为de Broglie波。 研究微观粒子的运动时,不能忽略其波动性。 微观粒子具有波粒二象性
式子的左侧动量 P 是表示粒子性的物理量,而右侧波长 是 表示波动性的物理量。二者通过公式联系起来。 de Broglie 认为具有动量P 的微观粒子,其物质波的波长 为 , P h = 1927 年, de Broglie 的预言被电子衍射实验所证实,这种物 质波称为 de Broglie 波。 = h P 研究微观粒子的运动时,不能忽略其波动性。 微观粒子具有波粒二象性
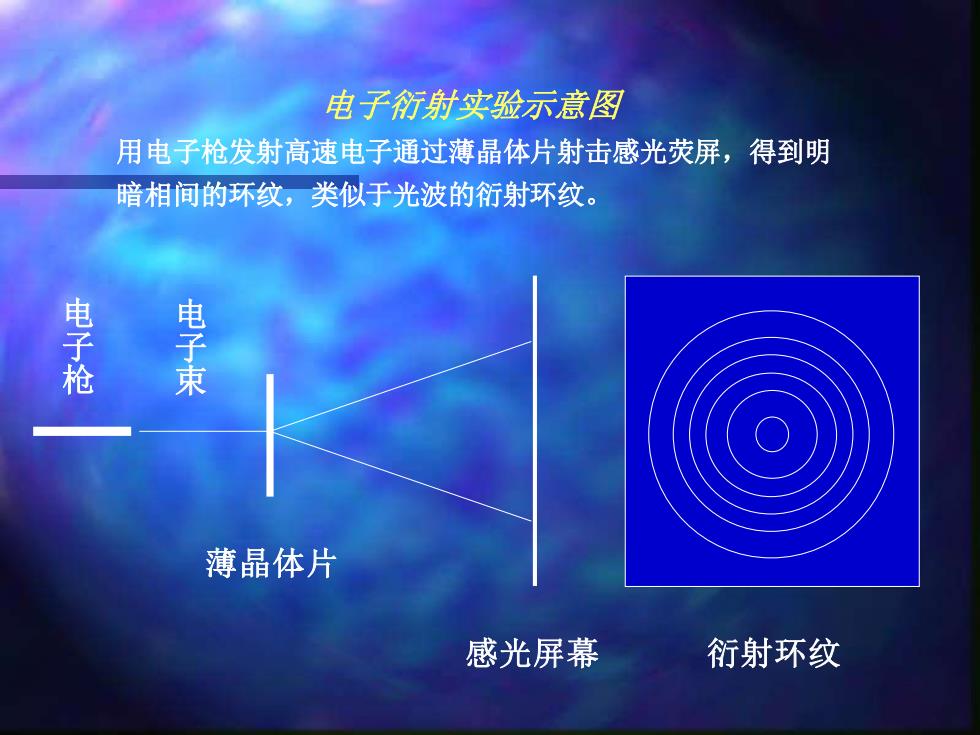
电子衍射实验示意图 用电子枪发射高速电子通过薄晶体片射击感光荧屏,得到明 暗相间的环纹,类似于光波的衍射环纹。 电子枪 电子束 薄晶体片 感光屏幕 衍射环纹
感光屏幕 薄晶体片 衍射环纹 电 子 枪 电 子 束 电子衍射实验示意图 用电子枪发射高速电子通过薄晶体片射击感光荧屏,得到明 暗相间的环纹,类似于光波的衍射环纹

四、Sohrodinger方程和波函数 波函数平的几何图象可以用来表示微观粒子活动的 区域。1926年,奥地利物理学家薛定谔提出了 (Sohrodinger)提出了薛定谔方程,波函数乎就是通过 解薛定谔方程得到的。 薛定谔方程 a2Ψa2Ψa2Ψ 8元m 63 (E-V)Ψ=0 (1) Ox2 z2 这是一个二阶偏微分方程 式中:平波函数,E能量,V势能,m微粒的质量, 元 圆周率,h普朗克常数
四、 Sohrodinger方程和波函数 波函数 的几何图象可以用来表示微观粒子活动的 区域。1926 年,奥地利物理学家薛定谔提出了 (Sohrodinger ) 提出了薛定谔方程,波函数 就是通过 解薛定谔方程得到的。 薛定谔方程 (E V) 0 (1) h 8 m x y z 2 2 2 2 2 2 2 2 − = + + + 这是一个二阶偏微分方程 式中: 波函数 ,E 能量 ,V 势能 ,m 微粒的质量, 圆周率 , h 普朗克常数

1.四个量子数及含义 波函数平的下标1,0,0;2,0,0;2,1,0所对应的 n,l,m,称为量子数。 (1) 主量子数n 取值:1,2,3,4..…n 为正整数(自然数), 光谱学上用K,L,M,N 表示。 意义表示原子轨道的大小,核外电子离核的远近,或者说 是电子所在的电子层数。n=1表示第一层(K层),离核最近。 m越大离核越远。 单电子体系,电子的能量由n决定E=-13.6× E 电子能量,Z原子序数, eV 电子伏特,能量单位,1eV=1.603×10-19J
1. 四个量子数及含义 波函数 的下标 1,0,0; 2,0,0;2,1,0 所对应的 n,l,m,称为量子数。 (1) 主量子数 n 取值: 1, 2, 3, 4 … … n 为正整数( 自然数 ) , 光谱学上用 K,L,M,N … … 表示 。 意义 表示原子轨道的大小,核外电子离核的远近,或者说 是电子所在的电子层数。n = 1 表示第一层 ( K 层 ) ,离核最近。 n 越大离核越远。 单电子体系,电子的能量由 n 决定 eV n Z E 13.6 2 2 = − E 电子能量,Z 原子序数, eV 电子伏特,能量单位,1 eV = 1.603 10-19 J

n的数值大,电子距离原子核远, 则具有较高的能量。 对于H原子 n= E=-13.6eV n=2E=-3.40eV n→cE=0即自由电子,其能量最大,为0。 主量子数1只能取1,2,3,4等自然数,故能量只有不连 续的几种取值,即能量是量子化的。所以称为量子数。 (2)角量子数1 取值受主量子数的限制,对于确定的主量子数n,角 量子数1可以为0,1,2,3,4….(n-1),共n个取值, 光谱学上依次用s,p,d,f,g…表示
对于 H 原子 n = 1 E = - 13.6 eV n = 2 E = - 3.40 eV … … n → E = 0 即自由电子,其能量最大,为0 。 n 的数值大,电子距离原子核远,则具有较高的能量。 主量子数 n 只能取 1,2,3,4 等自然数,故能量只有不连 续的几种取值,即能量是量子化的。所以 n 称为量子数。 (2) 角量子数 l 取值 受主量子数 n 的限制, 对于确定的主量子数n ,角 量子数 l 可以为 0,1,2,3,4 … … ( n - 1 ) , 共 n 个取值, 光谱学上依次用 s,p,d,f, g … … 表示