
第十一章 凸轮机构及其设计 §11-1 凸轮机构的应用和分类 §11-2 推杆的运动规律 §11-3 凸轮轮廓曲线的设计 §11-4 凸轮机构基本尺寸的确定
第十一章 凸轮机构及其设计 §11-1 凸轮机构的应用和分类 §11-2 推杆的运动规律 §11-3 凸轮轮廓曲线的设计 §11-4 凸轮机构基本尺寸的确定

§11-1 凸轮机构的应用和分类 结构特点:三个构件、盘(柱)状曲线轮廓、从动件呈杆状。 作用:将凸轮的连续回转转变为从动件直线移动或摆动。 优点:可精确实现任意运动规律,简单紧凑。 缺点:高副,线接触,易磨损,传力不大。 1)按凸轮形状分:盘形、移动、圆柱凸轮(端面) 。 应用:内燃机 、牙膏生产等自动线、补鞋机、配钥匙机等。 分类: 2)按推杆形状分:尖顶、 滚子、平底从动件。 3).按推杆运动分:直动(对心、偏置)、摆动 特点:尖顶--构造简单、易磨损、用于仪表机构; 滚子――磨损小,应用广; 平底――受力好、润滑好,用于高速传动。 4).按保持接触方式分:力封闭(重力、弹簧等) 几何形状封闭(凹槽、等宽、等径、主回凸轮) R字机构
§11-1 凸轮机构的应用和分类 结构特点:三个构件、盘(柱)状曲线轮廓、从动件呈杆状。 作用:将凸轮的连续回转转变为从动件直线移动或摆动。 优点:可精确实现任意运动规律,简单紧凑。 缺点:高副,线接触,易磨损,传力不大。 1)按凸轮形状分:盘形、移动、圆柱凸轮(端面) 。 应用:内燃机 、牙膏生产等自动线、补鞋机、配钥匙机等。 分类: 2)按推杆形状分:尖顶、 滚子、平底从动件。 3).按推杆运动分:直动(对心、偏置)、摆动 特点:尖顶--构造简单、易磨损、用于仪表机构; 滚子――磨损小,应用广; 平底――受力好、润滑好,用于高速传动。 4).按保持接触方式分:力封闭(重力、弹簧等) 几何形状封闭(凹槽、等宽、等径、主回凸轮) R字机构
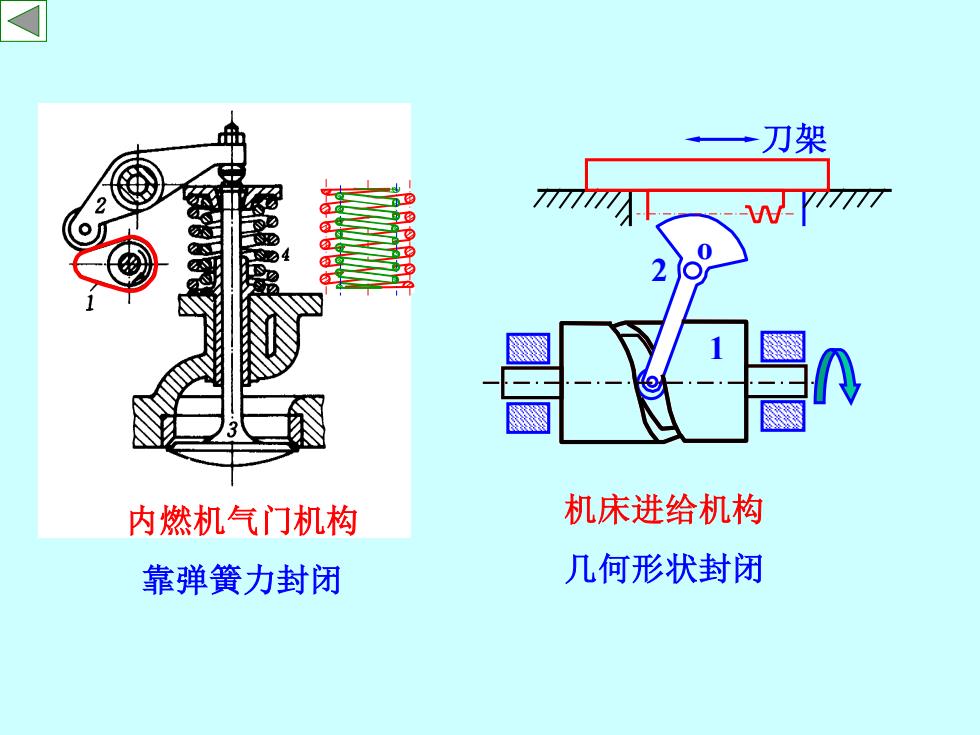
内燃机气门机构 靠弹簧力封闭 机床进给机构 几何形状封闭 1 2 刀架 o
内燃机气门机构 靠弹簧力封闭 机床进给机构 几何形状封闭 1 2 刀架 o
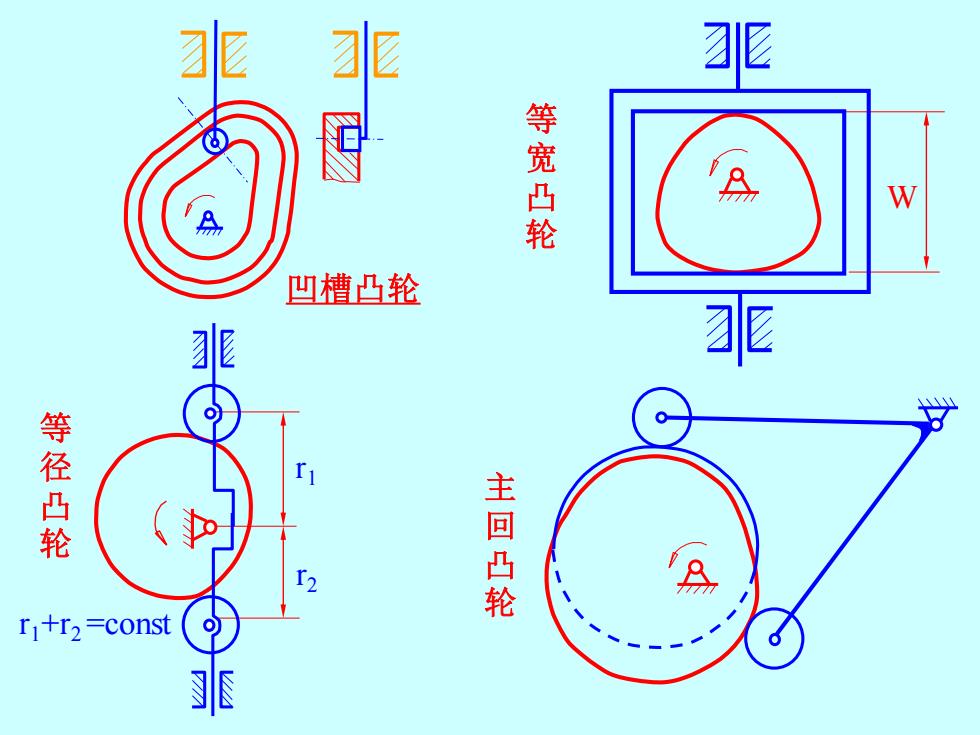
r 1 r 2 r 1+r2 =const W 凹槽凸轮 主回凸轮 等宽凸轮 等径凸轮
r 1 r 2 r 1+r2 =const W 凹槽凸轮 主回凸轮 等宽凸轮 等径凸轮
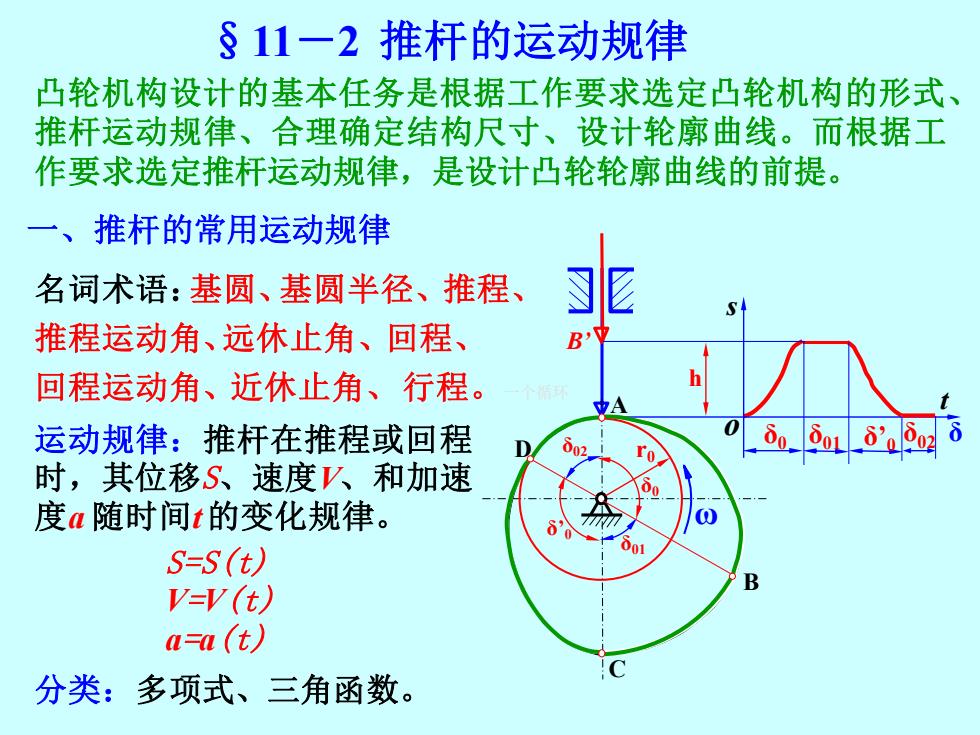
§11-2 推杆的运动规律 凸轮机构设计的基本任务是根据工作要求选定凸轮机构的形式、 推杆运动规律、合理确定结构尺寸、设计轮廓曲线。而根据工 作要求选定推杆运动规律,是设计凸轮轮廓曲线的前提。 名词术语: 运动规律:推杆在推程或回程 时,其位移S、速度V、和加速 度a 随时间t的变化规律。 分类:多项式、三角函数。 S=S(t) V=V(t) a=a(t) 一、推杆的常用运动规律 基圆、 推程运动角、 基圆半径、推程、 远休止角、 回程运动角、 回程、 近休止角、行程。一个循环 r0 h B’ o t δ s δ01 δ01 δ δ02 02 δ0 δ0 δ’0 δ’0 ω A D C B
§11-2 推杆的运动规律 凸轮机构设计的基本任务是根据工作要求选定凸轮机构的形式、 推杆运动规律、合理确定结构尺寸、设计轮廓曲线。而根据工 作要求选定推杆运动规律,是设计凸轮轮廓曲线的前提。 名词术语: 运动规律:推杆在推程或回程 时,其位移S、速度V、和加速 度a 随时间t的变化规律。 分类:多项式、三角函数。 S=S(t) V=V(t) a=a(t) 一、推杆的常用运动规律 基圆、 推程运动角、 基圆半径、推程、 远休止角、 回程运动角、 回程、 近休止角、行程。一个循环 r0 h B’ o t δ s δ01 δ01 δ δ02 02 δ0 δ0 δ’0 δ’0 ω A D C B

边界条件: 凸轮转过推程运动角δ0-从动件上升h 凸轮转过回程运动角δ’ 0-从动件下降h 1.多项式运动规律 一般表达式:s=C0+ C1δ+ C2δ2 +.+Cn δn (1) 求一阶导数得速度方程:v=ds/dt 求二阶导数得加速度方程: a =dv/dt =2 C2ω2 + 6C3ω2δ.+n(n-1)Cn ω2δn-2 其中:δ-凸轮转角,dδ/dt=ω-凸轮角速度, Ci-待定系数。 a)一次多项式(等速运动)运动规律 在推程起始点:δ=0, s=0 代入得:C0=0,C1=h/δ0 推程运动方程: s=hδ/δ0 v= hω/δ0 a=0 s δ0 δ v δ a δ h 在推程终止点:δ=δ0,s=h +∞ 刚性冲击 -∞ = C1ω+ 2C2ωδ+.+nCn ωδn-1
边界条件: 凸轮转过推程运动角δ0-从动件上升h 凸轮转过回程运动角δ’ 0-从动件下降h 1.多项式运动规律 一般表达式:s=C0+ C1δ+ C2δ2 +.+Cn δn (1) 求一阶导数得速度方程:v=ds/dt 求二阶导数得加速度方程: a =dv/dt =2 C2ω2 + 6C3ω2δ.+n(n-1)Cn ω2δn-2 其中:δ-凸轮转角,dδ/dt=ω-凸轮角速度, Ci-待定系数。 a)一次多项式(等速运动)运动规律 在推程起始点:δ=0, s=0 代入得:C0=0,C1=h/δ0 推程运动方程: s=hδ/δ0 v= hω/δ0 a=0 s δ0 δ v δ a δ h 在推程终止点:δ=δ0,s=h +∞ 刚性冲击 -∞ = C1ω+ 2C2ωδ+.+nCn ωδn-1

同理得回程运动方程: s=h(1-δ/δ’ 0 ) b)二次多项式(等加等减速)运动规律 位移曲线为一抛物线。加、减速各占一半。 推程加速上升段边界条件: 起始点:δ=0, s=0, v=0 中间点:δ=δ0/2,s=h/2 求得:C0=0,C1=0,C2=2h/δ0 2 加速段推程运动方程为: s =2hδ2 /δ0 2 推程减速上升段边界条件: 终止点:δ=δ0, s=h, v=0 中间点:δ=δ0/2,s=h/2 求得:C0=-h,C1=4h/δ0,C2=-2h/δ0 2 减速段推程运动方程为:s =h-2h(δ-δ0) 2 /δ0 2 1 δ s δ v δ a v =4hωδ/δ0 2 a =4hω2 /δ0 2 v =-4hω(δ-δ0)/δ0 2 a =-4hω2 /δ0 2 2 3 4 5 6 h/2 δ0 h/2 2hω/δ0 柔性冲击 4hω2 /δ0 2 50分 v=-hω/δ’ 0 a=0 3
同理得回程运动方程: s=h(1-δ/δ’ 0 ) b)二次多项式(等加等减速)运动规律 位移曲线为一抛物线。加、减速各占一半。 推程加速上升段边界条件: 起始点:δ=0, s=0, v=0 中间点:δ=δ0/2,s=h/2 求得:C0=0,C1=0,C2=2h/δ0 2 加速段推程运动方程为: s =2hδ2 /δ0 2 推程减速上升段边界条件: 终止点:δ=δ0, s=h, v=0 中间点:δ=δ0/2,s=h/2 求得:C0=-h,C1=4h/δ0,C2=-2h/δ0 2 减速段推程运动方程为:s =h-2h(δ-δ0) 2 /δ0 2 1 δ s δ v δ a v =4hωδ/δ0 2 a =4hω2 /δ0 2 v =-4hω(δ-δ0)/δ0 2 a =-4hω2 /δ0 2 2 3 4 5 6 h/2 δ0 h/2 2hω/δ0 柔性冲击 4hω2 /δ0 2 50分 v=-hω/δ’ 0 a=0 3
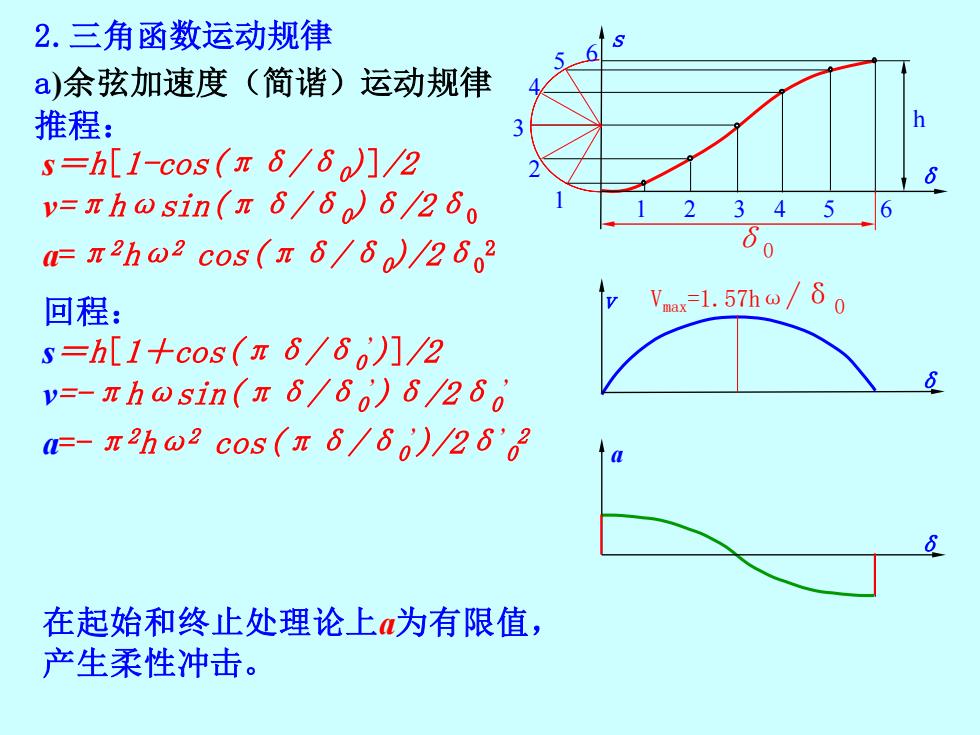
2.三角函数运动规律 a)余弦加速度(简谐)运动规律 推程: s=h[1-cos(πδ/δ0)]/2 v=πhωsin(πδ/δ0)δ/2δ0 a=π2 hω2 cos(πδ/δ0)/2δ0 2 回程: s=h[1+cos(πδ/δ0 ’)]/2 v=-πhωsin(πδ/δ0 ’)δ/2δ0 ’ a=-π2 hω2 cos(πδ/δ0 ’)/2δ’ 0 2 1 2 3 4 5 6 δ a δ v δ s h δ0 1 2 3 4 5 6 Vmax=1.57hω/δ0 在起始和终止处理论上a为有限值, 产生柔性冲击
2.三角函数运动规律 a)余弦加速度(简谐)运动规律 推程: s=h[1-cos(πδ/δ0)]/2 v=πhωsin(πδ/δ0)δ/2δ0 a=π2 hω2 cos(πδ/δ0)/2δ0 2 回程: s=h[1+cos(πδ/δ0 ’)]/2 v=-πhωsin(πδ/δ0 ’)δ/2δ0 ’ a=-π2 hω2 cos(πδ/δ0 ’)/2δ’ 0 2 1 2 3 4 5 6 δ a δ v δ s h δ0 1 2 3 4 5 6 Vmax=1.57hω/δ0 在起始和终止处理论上a为有限值, 产生柔性冲击
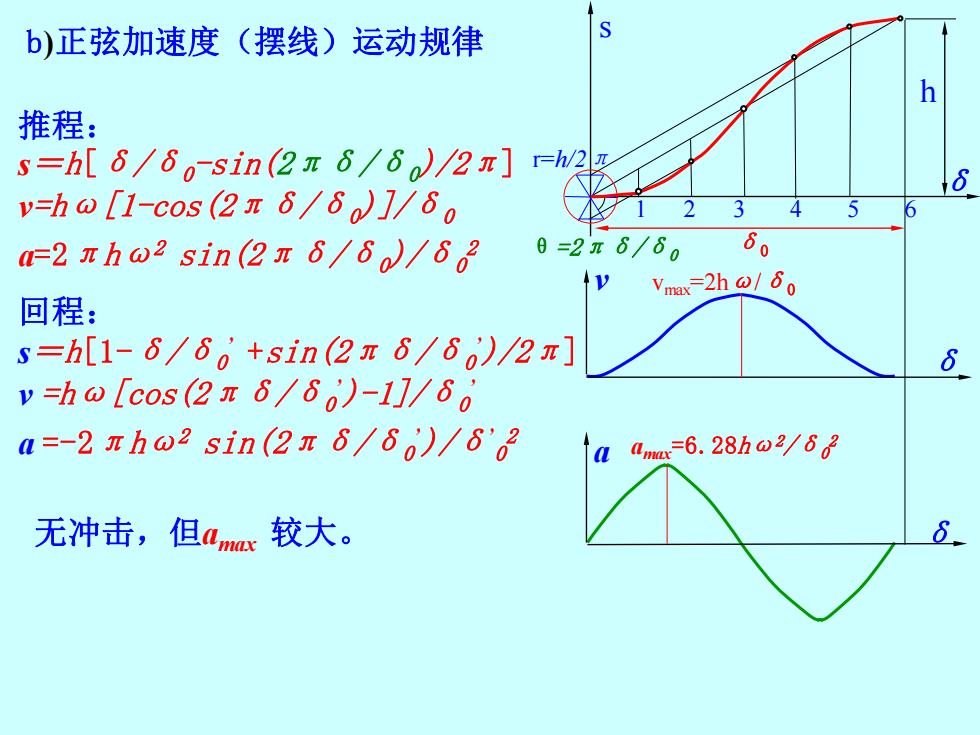
s δ b)正弦加速度(摆线)运动规律 推程: s=h[δ/δ0-sin(2πδ/δ0)/2π] v=hω[1-cos(2πδ/δ0)]/δ0 a=2πhω2 sin(2πδ/δ0)/δ0 2 回程: s=h[1-δ/δ0 ’ +sin(2πδ/δ0 ’)/2π] v =hω[cos(2πδ/δ0 ’)-1]/δ0 ’ a =-2πhω2 sin(2πδ/δ0 ’)/δ’ 0 2 1 2 3 4 5 6 v δ δ a h δ0 r=h/2π vmax=2hω/δ0 amax =6.28hω2 /δ0 2 无冲击,但amax 较大。 θ=2πδ/δ0
s δ b)正弦加速度(摆线)运动规律 推程: s=h[δ/δ0-sin(2πδ/δ0)/2π] v=hω[1-cos(2πδ/δ0)]/δ0 a=2πhω2 sin(2πδ/δ0)/δ0 2 回程: s=h[1-δ/δ0 ’ +sin(2πδ/δ0 ’)/2π] v =hω[cos(2πδ/δ0 ’)-1]/δ0 ’ a =-2πhω2 sin(2πδ/δ0 ’)/δ’ 0 2 1 2 3 4 5 6 v δ δ a h δ0 r=h/2π vmax=2hω/δ0 amax =6.28hω2 /δ0 2 无冲击,但amax 较大。 θ=2πδ/δ0
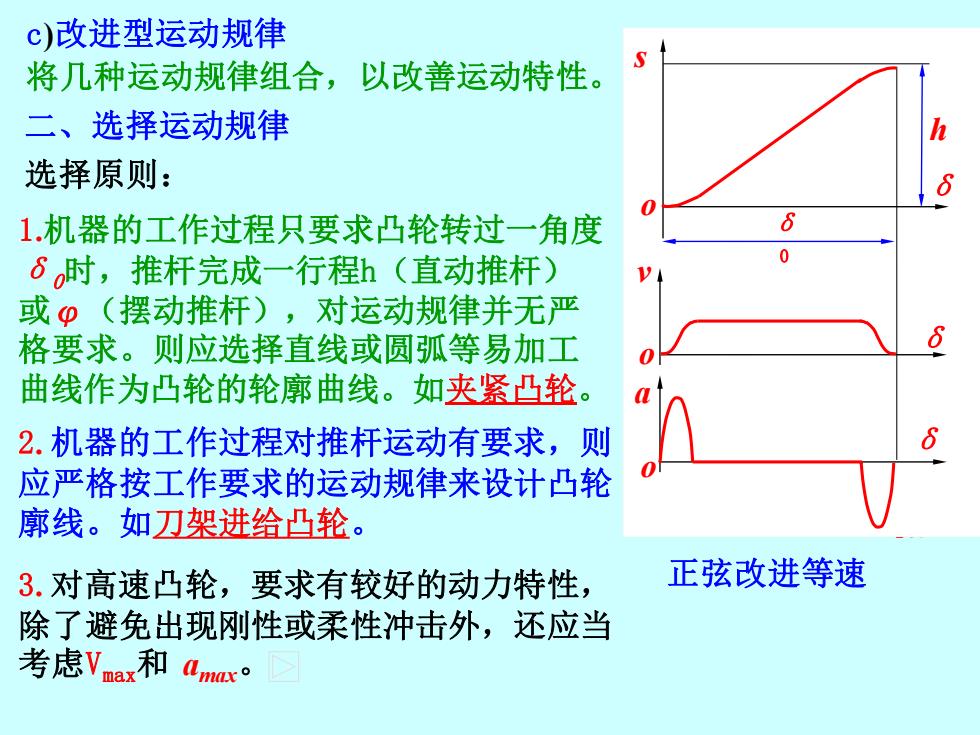
δ δ δ h v s a o o o δ 0 +∞ -∞ v s a δ δ δ h o o o δ 0 c)改进型运动规律 将几种运动规律组合,以改善运动特性。 正弦改进等速 二、选择运动规律 选择原则: 1.机器的工作过程只要求凸轮转过一角度 δ0时,推杆完成一行程h(直动推杆) 或φ(摆动推杆),对运动规律并无严 格要求。则应选择直线或圆弧等易加工 曲线作为凸轮的轮廓曲线。如夹紧凸轮。 2. 机器的工作过程对推杆运动有要求,则 应严格按工作要求的运动规律来设计凸轮 廓线。如刀架进给凸轮。 3. 对高速凸轮,要求有较好的动力特性, 除了避免出现刚性或柔性冲击外,还应当 考虑Vmax和 amax
δ δ δ h v s a o o o δ 0 +∞ -∞ v s a δ δ δ h o o o δ 0 c)改进型运动规律 将几种运动规律组合,以改善运动特性。 正弦改进等速 二、选择运动规律 选择原则: 1.机器的工作过程只要求凸轮转过一角度 δ0时,推杆完成一行程h(直动推杆) 或φ(摆动推杆),对运动规律并无严 格要求。则应选择直线或圆弧等易加工 曲线作为凸轮的轮廓曲线。如夹紧凸轮。 2. 机器的工作过程对推杆运动有要求,则 应严格按工作要求的运动规律来设计凸轮 廓线。如刀架进给凸轮。 3. 对高速凸轮,要求有较好的动力特性, 除了避免出现刚性或柔性冲击外,还应当 考虑Vmax和 amax