
第 十 五 章 链 传 动
第 十 五 章 链 传 动

挠性传动 链条变形 1.链传动的组成和特点 链条 组成 链轮(主、从) 啮合传动 特点: 效率高 平均 i 准确 承载大 瞬时链速、i 变化 冲击、噪音、不平稳 i<8、P<100 kN、v <12~ 15m/s 2.应用 附加动载荷 大中心距、重载、条件恶劣 齿形链 曳引链 3.分类 起重链 滚动链 传动链
挠性传动 链条变形 1.链传动的组成和特点 链条 组成 链轮(主、从) 啮合传动 特点: 效率高 平均 i 准确 承载大 瞬时链速、i 变化 冲击、噪音、不平稳 i<8、P<100 kN、v <12~ 15m/s 2.应用 附加动载荷 大中心距、重载、条件恶劣 齿形链 曳引链 3.分类 起重链 滚动链 传动链
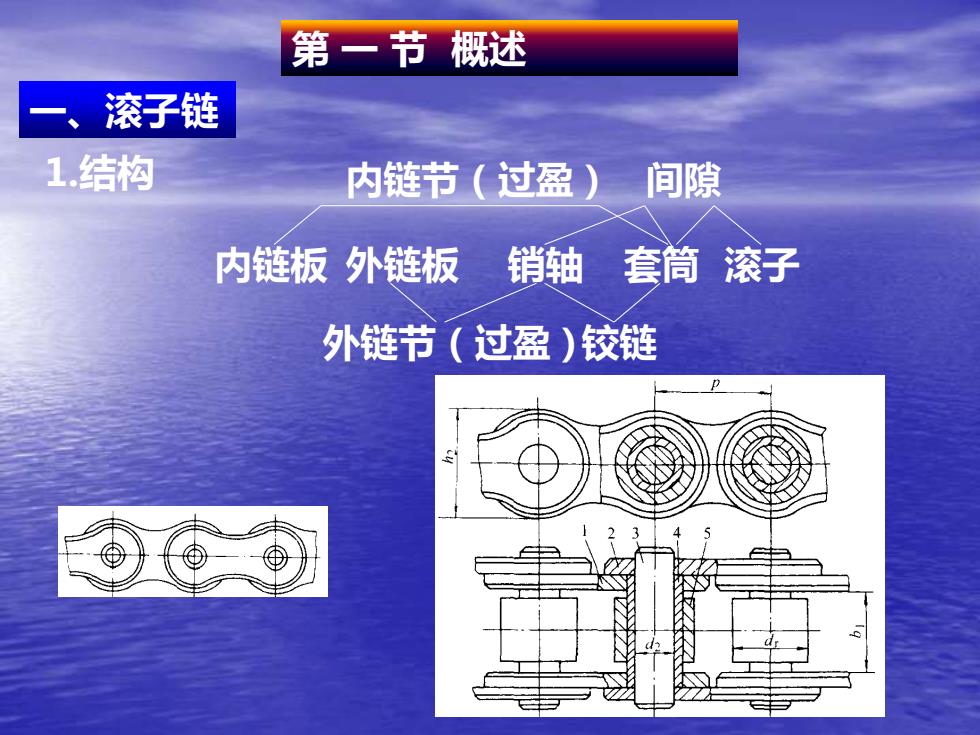
一、滚子链 内链板 第 一 节 概述 套筒 1.结构 外链板 销轴 滚子 内链节(过盈) 间隙 外链节(过盈)铰链
一、滚子链 内链板 第 一 节 概述 套筒 1.结构 外链板 销轴 滚子 内链节(过盈) 间隙 外链节(过盈)铰链
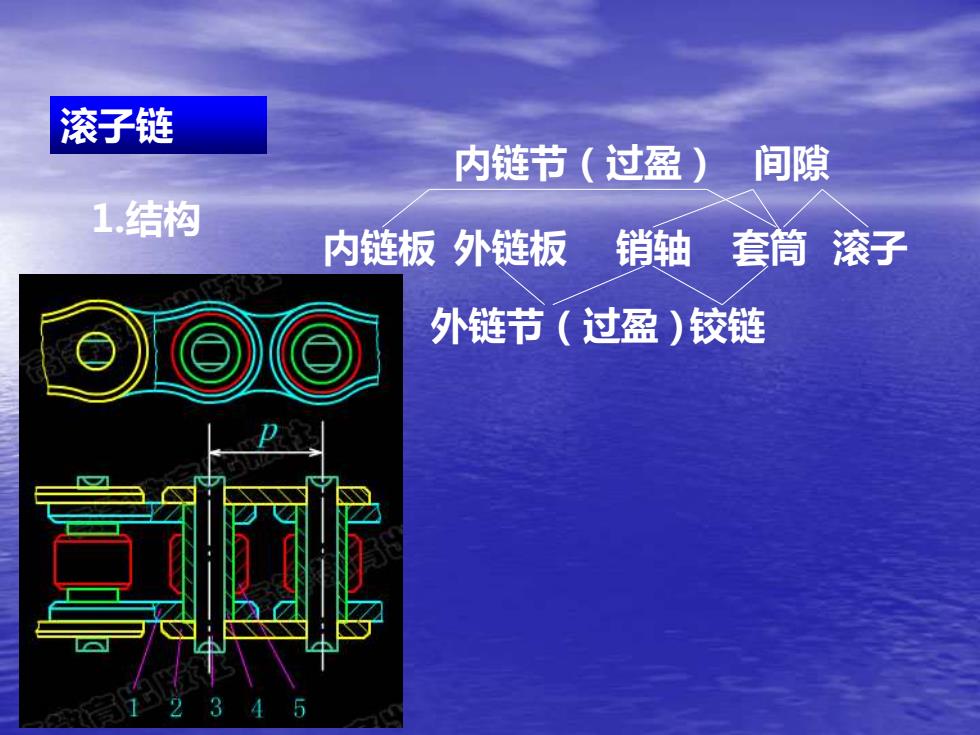
滚子链 内链板 套筒 1.结构 外链板 销轴 滚子 内链节(过盈) 间隙 外链节(过盈)铰链
滚子链 内链板 套筒 1.结构 外链板 销轴 滚子 内链节(过盈) 间隙 外链节(过盈)铰链

Lp=L/p 相邻两滚子中心的距离 ⑵节数Lp 选偶数 2.标准 p 大,载荷大,尺寸大。 p 小,可采用多排链(1~3) ⑴节距p ⑶标记 奇数:过渡链节 例如:A系列:节距25.4mm、单排、90节的滚子链。 排数 弹簧夹 开口销 (锁紧) 相接处 p 大 p 小 标准编号 - × 链号 链节数 16A-1×90GB1234.1- 83
Lp=L/p 相邻两滚子中心的距离 ⑵节数Lp 选偶数 2.标准 p 大,载荷大,尺寸大。 p 小,可采用多排链(1~3) ⑴节距p ⑶标记 奇数:过渡链节 例如:A系列:节距25.4mm、单排、90节的滚子链。 排数 弹簧夹 开口销 (锁紧) 相接处 p 大 p 小 标准编号 - × 链号 链节数 16A-1×90GB1234.1- 83
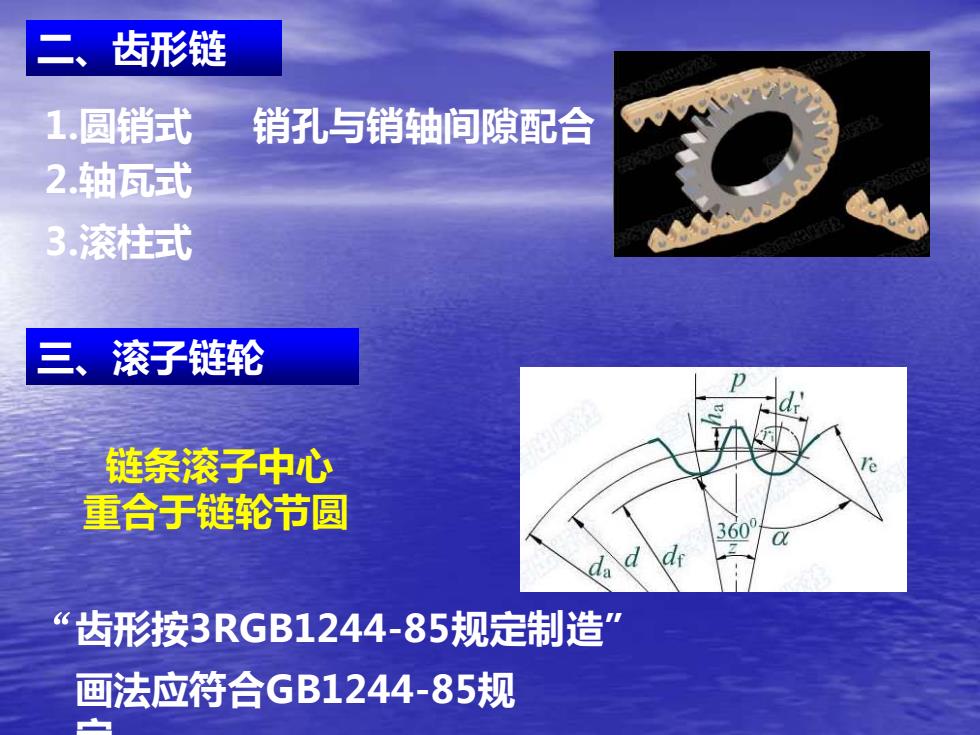
二、齿形链 三、滚子链轮 销孔与销轴间隙配合 2.轴瓦式 1.圆销式 “齿形按3RGB1244-85规定制造” 3.滚柱式 画法应符合GB1244-85规 定 链条滚子中心 重合于链轮节圆
二、齿形链 三、滚子链轮 销孔与销轴间隙配合 2.轴瓦式 1.圆销式 “齿形按3RGB1244-85规定制造” 3.滚柱式 画法应符合GB1244-85规 定 链条滚子中心 重合于链轮节圆

奇数 分度圆直径 齿根圆直径 dr——滚子外径 LX= df 偶数 df = d-dr 最大齿根距离 齿顶圆直径 2.链轮的材料 小轮材料的强度、硬度要高于大轮 1.尺寸 Z o p d 180 sin = ( . cot ) Z o da p 1 8 0 = 0 5 4+ Z r o X L d -d 9 0 = c os Z——链轮齿 数
奇数 分度圆直径 齿根圆直径 dr——滚子外径 LX= df 偶数 df = d-dr 最大齿根距离 齿顶圆直径 2.链轮的材料 小轮材料的强度、硬度要高于大轮 1.尺寸 Z o p d 180 sin = ( . cot ) Z o da p 1 8 0 = 0 5 4+ Z r o X L d -d 9 0 = c os Z——链轮齿 数

3.链轮结构 实心式 孔板式 焊接式 组合式
3.链轮结构 实心式 孔板式 焊接式 组合式
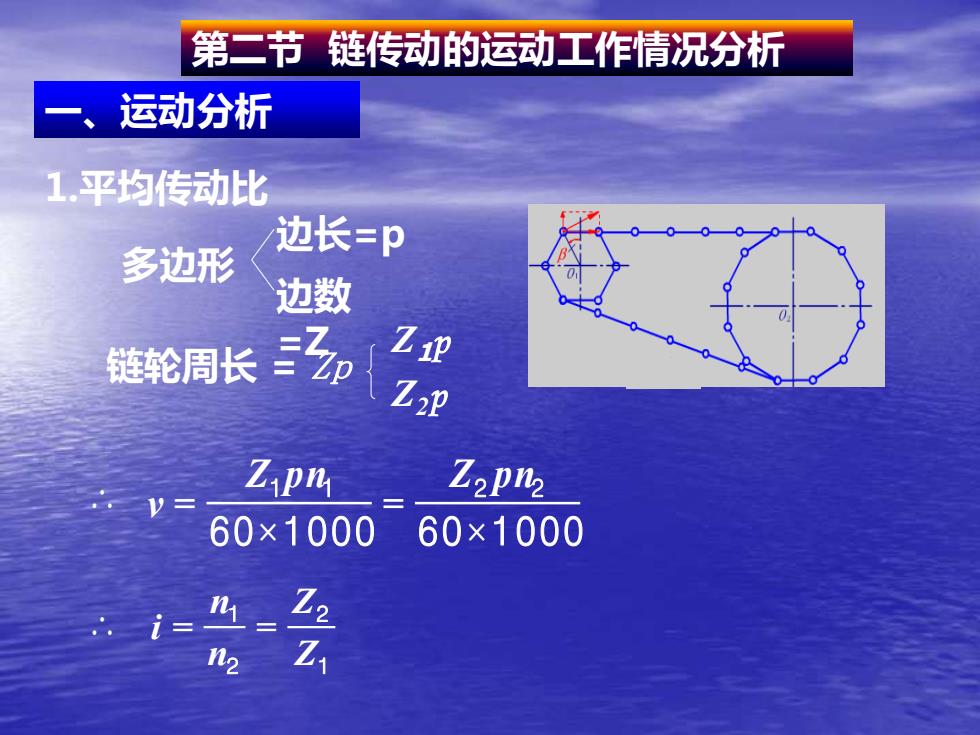
第二节 链传动的运动工作情况分析 1.平均传动比 一、运动分析 边长=p 多边形 边数 =Z 链轮周长 = Zp Z1p Z2p ∴ 6 0 1000 6 0 1000 1 1 2 2 × = × = Z p n Z p n v ∴ 1 2 2 1 Z Z n n i = =
第二节 链传动的运动工作情况分析 1.平均传动比 一、运动分析 边长=p 多边形 边数 =Z 链轮周长 = Zp Z1p Z2p ∴ 6 0 1000 6 0 1000 1 1 2 2 × = × = Z p n Z p n v ∴ 1 2 2 1 Z Z n n i = =

2.瞬时传动比 ⑴瞬时链速 设链条紧边始终处于水平 结论 瞬时链速随角β的变化作周期性变化 2 1 1 1 d ω v = 链速 β ω c osβ c os 2 1 1 1 d v = v = 1 1 180 180 Z Z O O - ≤ β≤ 当β=0°时 2 1 ω1 d v = v max = 当 时 1 180 Z o β= ± 1 1 1 180 2 Z d v v o min c os ω = =
2.瞬时传动比 ⑴瞬时链速 设链条紧边始终处于水平 结论 瞬时链速随角β的变化作周期性变化 2 1 1 1 d ω v = 链速 β ω c osβ c os 2 1 1 1 d v = v = 1 1 180 180 Z Z O O - ≤ β≤ 当β=0°时 2 1 ω1 d v = v max = 当 时 1 180 Z o β= ± 1 1 1 180 2 Z d v v o min c os ω = =