
Hydraulics 水力学 第十二章液体三元流理论基础 Three-dimensional flow of liquid 吕宏兴

§12.1概述 ·第三章中我们应用一元总流分析方法求得 渐变流过水断面上流速的平均值、压强的 分布以及液流作用于固壁周界上的总作用 力,这种分析方法忽略了液体的横向和竖 向运动,用断面平均流速来描述液体沿流 动方向的运动,反映了液体运动的基本规 律,可以用来解决工程水力学中大量实际 生产问题

§12.1概述 ·实践中也有许多问题单靠一元流的分析方法是 无能为力的,例如,分析河道、港湾中水流的流 态与冲淤变化,需要了解流场中的流速分布;分 析水流能量损失,需要研究水流内部结构等等。 这些问题都有必要研究整个流场中各个运动要素 的变化规律,而实际液体流动一般多属于三元流 动范畴,如果问题涉及流场中水力要素的分布或 研究液流内部结构等,就要应用流场分析法来解 决。本章主要介绍液体三元流的基本理论,并建 立反映液体三元流动普遍规律的微分方程

§12.2运动液体质点的速度、加速度 ·速度是液体质点的位移对时间的变化率,加速度则是 液体质点的速度对时间的变化率。 液体质点通过任意空间固定点(化,y,)时的流速 4.=4(x,y,z,t) u,=u,(x,y,z,t) (化,以,云,t):欧拉变数 (44,4):通过固定点的流速分量 u,=u(x,y,z,t) 1==给定时刻,(x,y,z)=变数 同一时刻,不同空间点上液体质点的流速分布,即流场 法 (x,y,z)=给定点,t=变数 不同液体质点通过给定空间点的流速变化
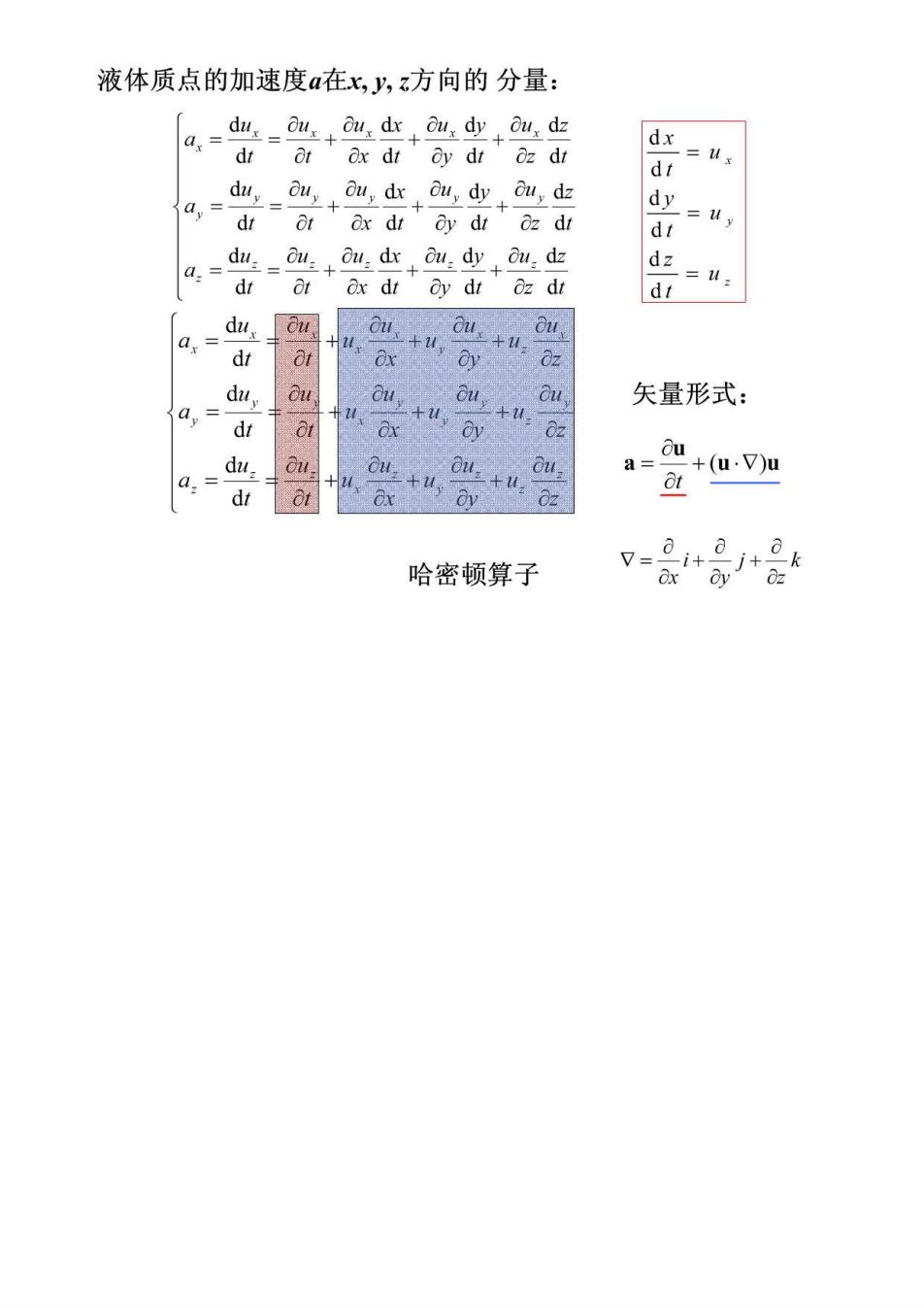
液体质点的加速度a在x,,z方向的分量: a,= du ouou dx ou,dy ou,dz dx dr ot &x dt dy dr oz dr di =4 du,ou,ou,dx ou,dy ou,dz a,= dy dt ot ox dt oy dr oz dr dr a, du-ou+audr+ud业+ou:d业 dz dr or dx dr dy dt dz dr dt = du a. dr du 矢量形式: a du. ou. a= d,= u+uV加 d山 哈密顿算子 v=040 Ox

加速度a的矢量形式: a _0u+(u.V)u ot >时变加速度或当地加速度:如 固定点上时间变化引起的加速度 同一空间点,不同时刻,流速不同,而产生的加速度 >位变加速度或迁移加速度:(u.V)u 空间位置变化引起的加速度。 同一时刻,不同空间点上流速不同,而产生的加速度 哈密顿算子v是:号+是
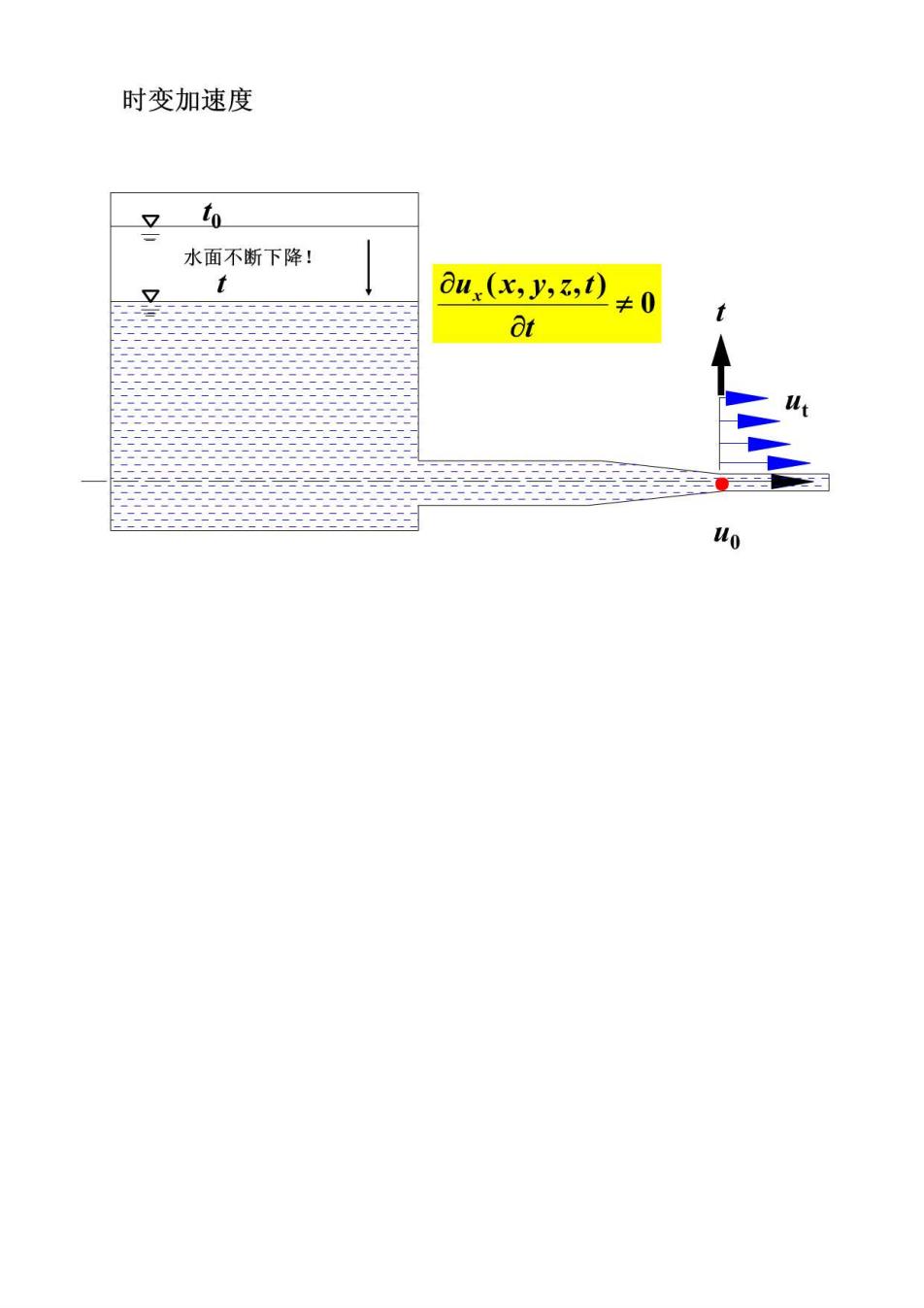
时变加速度 水面不断下降! t au.(x,y,3,2≠0

位变加速度 水面保持恒定 au,(x,y,z,0+0 Ox
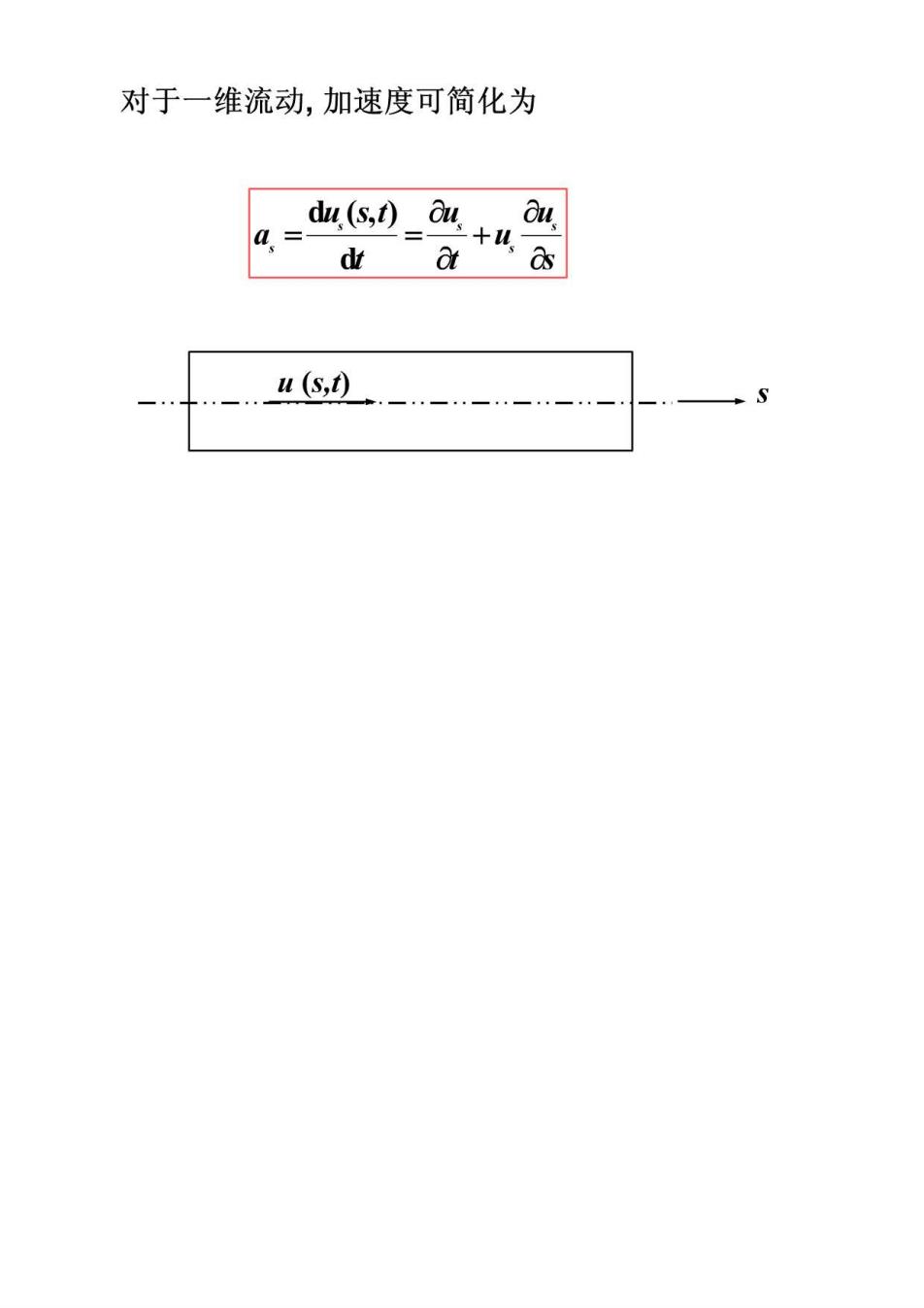
对于一维流动,加速度可简化为 .= du (s1) dt at u(s,)

§12.3迹线和流线 ·拉格朗日法中位移 ·迹线是液体 表达式 质点运动的轨 r=r(a,b,c,t) 迹,是与拉格 即为迹线的参数方 朗日观点相对 程。 应的概念。 t是变数,a,b,c是 参数