
《数学软件与实验》教学大纲 课程编码:110825 课程名称:数学软件与实验 学时/学分:54/3 先修课程:《数学分析》、《高等代数》、《解析几何》 适用专业:数学与应用数学 开课教研室:应用数学教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的专业必修课、理论与实践课。本课程开 设在第4学期。 2.课程任务:通过本课程的学习,使学生熟练掌握Matlab软件的基本知识,能够用 Mat1b软件编写程序进行数值计算、符号计算、作图等常见数学运算。同时,使学生学 握数学实验的基本方法和思想,培养学生从问题出发,借助于计算机与数学软件,自己设 计和动手,体验解决问题的过程,从实验中去学习、探索和发现数学规律,激发学生学习 数学的兴趣。 二、课程教学基本要求 该课程是一门具有较强实践性的课程,是理论教学的深化与补充,主要借助于数学软件 进行计算、作图等数学运算,加深学生对数学知识的掌握和理解,提高学生综合应用数学知 识、数学软件和计算机技术解决实际问题的能力。教学过程采用讲授与练习相结合、理论推 导及运算与上机操作相结合的方式。通常在课程的开始时先用一定课时介绍数学软件的基本 内容和操作指令,并要求学生进行适当的课题练习,作为后继实验内容的基础:在每一个探 究型实验或应用型实验开始时,先由教师授课约2学时,介绍实验问题的背景和基本原理, 以及相关的算法,然后布置实验任务,学生讨论、探究与建模,设计处理方案。 该课程共54学时,其中理论讲授36学时,课内实践18学时。 成绩考核形式:末考成绩(闭卷考查)(70%)+平时成绩(实验报告、课堂提问、课堂 讨论等)(30%)。成绩评定采用百分制,60分为及格。 三、课程教学内容 第一章Matlab与矩阵运算 1.教学基本要求 了解Matlab软件发展历史和特点,掌握Matlab软件基础知识,初步具备运用Matlab 软件编写程序解决实际问题的能力
《数学软件与实验》教学大纲 课程编码:110825 课程名称:数学软件与实验 学时/学分:54/3 先修课程:《数学分析》、《高等代数》、《解析几何》 适用专业:数学与应用数学 开课教研室:应用数学教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的专业必修课、理论与实践课。本课程开 设在第 4 学期。 2.课程任务:通过本课程的学习,使学生熟练掌握 Matlab 软件的基本知识,能够用 Matlab 软件编写程序进行数值计算、符号计算、作图等常见数学运算。同时,使学生掌 握数学实验的基本方法和思想,培养学生从问题出发,借助于计算机与数学软件,自己设 计和动手,体验解决问题的过程,从实验中去学习、探索和发现数学规律,激发学生学习 数学的兴趣。 二、课程教学基本要求 该课程是一门具有较强实践性的课程,是理论教学的深化与补充,主要借助于数学软件 进行计算、作图等数学运算,加深学生对数学知识的掌握和理解,提高学生综合应用数学知 识、数学软件和计算机技术解决实际问题的能力。教学过程采用讲授与练习相结合、理论推 导及运算与上机操作相结合的方式。通常在课程的开始时先用一定课时介绍数学软件的基本 内容和操作指令,并要求学生进行适当的课题练习,作为后继实验内容的基础;在每一个探 究型实验或应用型实验开始时,先由教师授课约 2 学时,介绍实验问题的背景和基本原理, 以及相关的算法,然后布置实验任务,学生讨论、探究与建模,设计处理方案。 该课程共 54 学时,其中理论讲授 36 学时,课内实践 18 学时。 成绩考核形式:末考成绩(闭卷考查)(70%)+平时成绩(实验报告、课堂提问、课堂 讨论等)(30%)。成绩评定采用百分制,60 分为及格。 三、课程教学内容 第一章 Matlab 与矩阵运算 1.教学基本要求 了解 Matlab 软件发展历史和特点,掌握 Matlab 软件基础知识,初步具备运用 Matlab 软件编写程序解决实际问题的能力

2.要求学生掌握的基本概念、理论、技能 通过本章教学,使学生熟悉Matlab的数据类型,掌握数组和符号对象的基本运算:掌 握顺序结构、循环结构、选择结构三种W文件流程控制语句,熟悉Matlab程序设计中基本 的交互语句,能够编简单at1b程序:掌握绘制二维和三维图形的方法。 3.教学重点和难点 教学重点是数组的操作及运算:逻辑运算与关系运算:符号运算:Mat1ab绘图:循环 结构和控制结构:基本的程序设计方法:M文件(脚本文件和函数文件)的编写。 教学难点是M文件(脚本文件和函数文件)的编写。 4.教学内容 第一节Matlab的基本操作 1.atlab发展历史、主要功能 2.atlab的安装 3.Matlab操作界面及主要窗口介绍 4.Command Window操作 5.数组的赋值与访问 6。矩阵和数组的常见运算函数 7.Matlab帮助系统 第二节 M文件与程序流程的控制 1.M文件简介 2.Matlab函数文件的编写 3.循环与控制 第三节 Matlab绘图 1.二维图形绘制 2.三维图形绘制 3.特殊图像绘制 4.图形修饰 第四节 线性代数 1.解线性方程组 2.特征值与特征向量、矩阵的对角化 第五节 符号计算 1.符号变量及基本运算 2.极限、微积分问题 3.级数问题 4.方程(组)求解
2.要求学生掌握的基本概念、理论、技能 通过本章教学,使学生熟悉 Matlab 的数据类型,掌握数组和符号对象的基本运算;掌 握顺序结构、循环结构、选择结构三种 M 文件流程控制语句,熟悉 Matlab 程序设计中基本 的交互语句,能够编简单 Matlab 程序;掌握绘制二维和三维图形的方法。 3.教学重点和难点 教学重点是数组的操作及运算;逻辑运算与关系运算;符号运算;Matlab 绘图;循环 结构和控制结构;基本的程序设计方法;M 文件(脚本文件和函数文件)的编写。 教学难点是 M 文件(脚本文件和函数文件)的编写。 4.教学内容 第一节 Matlab 的基本操作 1. Matlab 发展历史、主要功能 2. Matlab 的安装 3. Matlab 操作界面及主要窗口介绍 4. Command Window 操作 5. 数组的赋值与访问 6. 矩阵和数组的常见运算函数 7. Matlab 帮助系统 第二节 M 文件与程序流程的控制 1. M 文件简介 2. Matlab 函数文件的编写 3. 循环与控制 第三节 Matlab 绘图 1. 二维图形绘制 2. 三维图形绘制 3. 特殊图像绘制 4. 图形修饰 第四节 线性代数 1. 解线性方程组 2. 特征值与特征向量、矩阵的对角化 第五节 符号计算 1. 符号变量及基本运算 2. 极限、微积分问题 3. 级数问题 4. 方程(组)求解

5.符号函数作图 第六节 概率论与数理统计 1.随机数及概率 2.统计作图 3.常见分布的参数估计 4.假设检验 第二章 数值计算问题 1.教学基本要求 掌握用Matlab软件编写程序进行数值计算的方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生了解数学实验的基本思想,掌握用Matlab软件求方程近似根 数值积分、求微分方程解、插值与拟合等数值计算问题的方法,培养学生用数学软件分析 解决数学问题的能力。 3.教学重点和难点 教学重点是Matlab编程求方程近似根:atlab编程求数值积分,Mat1ab编程求常微分 方程的解,用atlb软件进行插值与拟合。 教学难点是各种数值计算问题的Matlab程序 4.教学内容 第一节求函数方程的近似实根 1.二分法 2.不动点迭代法 3.牛顿法及其改进形式 4.at1ab编程求解函数方程近似实根示例程序 5.Matlab的求函数值命令小结 第二节数值积分 1.常用数值积分方法 2.atlab计算定积分示例程序 3.at1ab中的数值积分命今 第三节 圆周率π的计算 1.古典方法 2.数值积分法 3.无穷级数法 4.其他计算π值计算公式
5. 符号函数作图 第六节 概率论与数理统计 1. 随机数及概率 2. 统计作图 3. 常见分布的参数估计 4. 假设检验 第二章 数值计算问题 1.教学基本要求 掌握用 Matlab 软件编写程序进行数值计算的方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,使学生了解数学实验的基本思想,掌握用 Matlab 软件求方程近似根、 数值积分、求微分方程解、插值与拟合等数值计算问题的方法,培养学生用数学软件分析、 解决数学问题的能力。 3.教学重点和难点 教学重点是 Matlab 编程求方程近似根;Matlab 编程求数值积分,Matlab 编程求常微分 方程的解,用 Matlab 软件进行插值与拟合。 教学难点是各种数值计算问题的 Matlab 程序。 4.教学内容 第一节 求函数方程的近似实根 1. 二分法 2. 不动点迭代法 3. 牛顿法及其改进形式 4. Matlab 编程求解函数方程近似实根示例程序 5. Matlab 的求函数值命令小结 第二节 数值积分 1.常用数值积分方法 2. Matlab 计算定积分示例程序 3. Matlab 中的数值积分命令 第三节 圆周率 的计算 1. 古典方法 2. 数值积分法 3. 无穷级数法 4. 其他计算 值计算公式

第四节 微分方程数值解法 1.引例:导弹追踪问题 2。微分方程及微分方程组的解析解法 3.微分方程的数值解 4.导弹追踪问题求解 第五节 插值问题 1.插值的概念和常见方法 2.at1ab软件计算各种插值的方法 第六节 曲线拟合 1.曲线拟合的基本原理 2.线性拟合 3.多项式拟合 4.一般形式的拟合 5.经验曲线(非线性拟合) 第三章 迭代一从金融问题到混沌现象 1.教学基本要求 了解迭代问题的计算方法和分形作图的基本步骤。 2.要求学生掌握的基本概念、理论、技能 3.教学重点和难点 4.教学内容 第一节 人口模型与存贷款问题 ,Malthus人口模型 2.存贷款问题 第二节分形作图 1.由生成元产生的分形图形 2.由迭代函数系FS)所生成的分形图形 3.由复变函数迭代所产生的分形图形 第四章 计算机模拟与仿真 1.教学基本要求 掌握用Matlab软件计算机模拟的方法,了解Simulink仿真基本操作 2.要求学生掌握的基本概念、理论、技能 通过本章学习,通过本章掌握用Mat1ab软件计算机模拟的基本原理和方法,并能通过
第四节 微分方程数值解法 1. 引例:导弹追踪问题 2. 微分方程及微分方程组的解析解法 3. 微分方程的数值解 4. 导弹追踪问题求解 第五节 插值问题 1. 插值的概念和常见方法 2. Matlab 软件计算各种插值的方法 第六节 曲线拟合 1. 曲线拟合的基本原理 2. 线性拟合 3. 多项式拟合 4. 一般形式的拟合 5. 经验曲线(非线性拟合) 第三章 迭代——从金融问题到混沌现象 1.教学基本要求 了解迭代问题的计算方法和分形作图的基本步骤。 2.要求学生掌握的基本概念、理论、技能 3.教学重点和难点 4.教学内容 第一节 人口模型与存贷款问题 1. Malthus 人口模型 2. 存贷款问题 第二节 分形作图 1. 由生成元产生的分形图形 2. 由迭代函数系(IFS)所生成的分形图形 3. 由复变函数迭代所产生的分形图形 第四章 计算机模拟与仿真 1.教学基本要求 掌握用 Matlab 软件计算机模拟的方法,了解 Simulink 仿真基本操作。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,通过本章掌握用 Matlab 软件计算机模拟的基本原理和方法,并能通过

计算机模拟解决实际问题。 3.教学重点和难点 教学重点是蒙特卡洛模拟原理:随机数字的生成:Mat1ab软件计算机模拟的方法。 教学难点是如何将实际问题转化为合适的数学模型。 4.教学内容 第一节计算机模拟 1.确定性系统模拟的例了 2.随机系统模拟的例子 第二节Simulink建模与仿真 1.Simulink工具箱及其操作简介 2.仿真示例 第五章 线性回归问题 1.教学基本要求 掌握用atlab软件处理回归分析的的方法,了解回归分析基础知识。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,通过本章掌握polyfit和regress命令的基本用法,并能用回归分析方 法分析解决实际问题。 3.教学重点和难点 教学重点是掌握Matlab软件作回归分析的方法。 教学难点是逐步回归的思想和方法。 4.教学内容 第一节 一元线性回归 1.一元线性回归基本概念 2.Matlab求解一元线性回归方法及示例 第二节多元线性回归 1.多元线性回归基本概念 2.atlb求解多元线性回归方法及示例 3.逐步回归基本思想及示例 四、学时分配 1.讲授内容及学时分配 章序 内容 课时 备注 MATLAB与矩阵运算 14
计算机模拟解决实际问题。 3.教学重点和难点 教学重点是蒙特卡洛模拟原理;随机数字的生成;Matlab 软件计算机模拟的方法。 教学难点是如何将实际问题转化为合适的数学模型。 4.教学内容 第一节 计算机模拟 1. 确定性系统模拟的例子 2. 随机系统模拟的例子 第二节 Simulink 建模与仿真 1. Simulink 工具箱及其操作简介 2. 仿真示例 第五章 线性回归问题 1.教学基本要求 掌握用 Matlab 软件处理回归分析的的方法,了解回归分析基础知识。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,通过本章掌握 polyfit 和 regress 命令的基本用法,并能用回归分析方 法分析解决实际问题。 3.教学重点和难点 教学重点是掌握 Matlab 软件作回归分析的方法。 教学难点是逐步回归的思想和方法。 4.教学内容 第一节 一元线性回归 1. 一元线性回归基本概念 2. Matlab 求解一元线性回归方法及示例 第二节 多元线性回归 1. 多元线性回归基本概念 2. Matlab 求解多元线性回归方法及示例 3. 逐步回归基本思想及示例 四、学时分配 1.讲授内容及学时分配 章序 内容 课时 备注 一 MATLAB 与矩阵运算 14
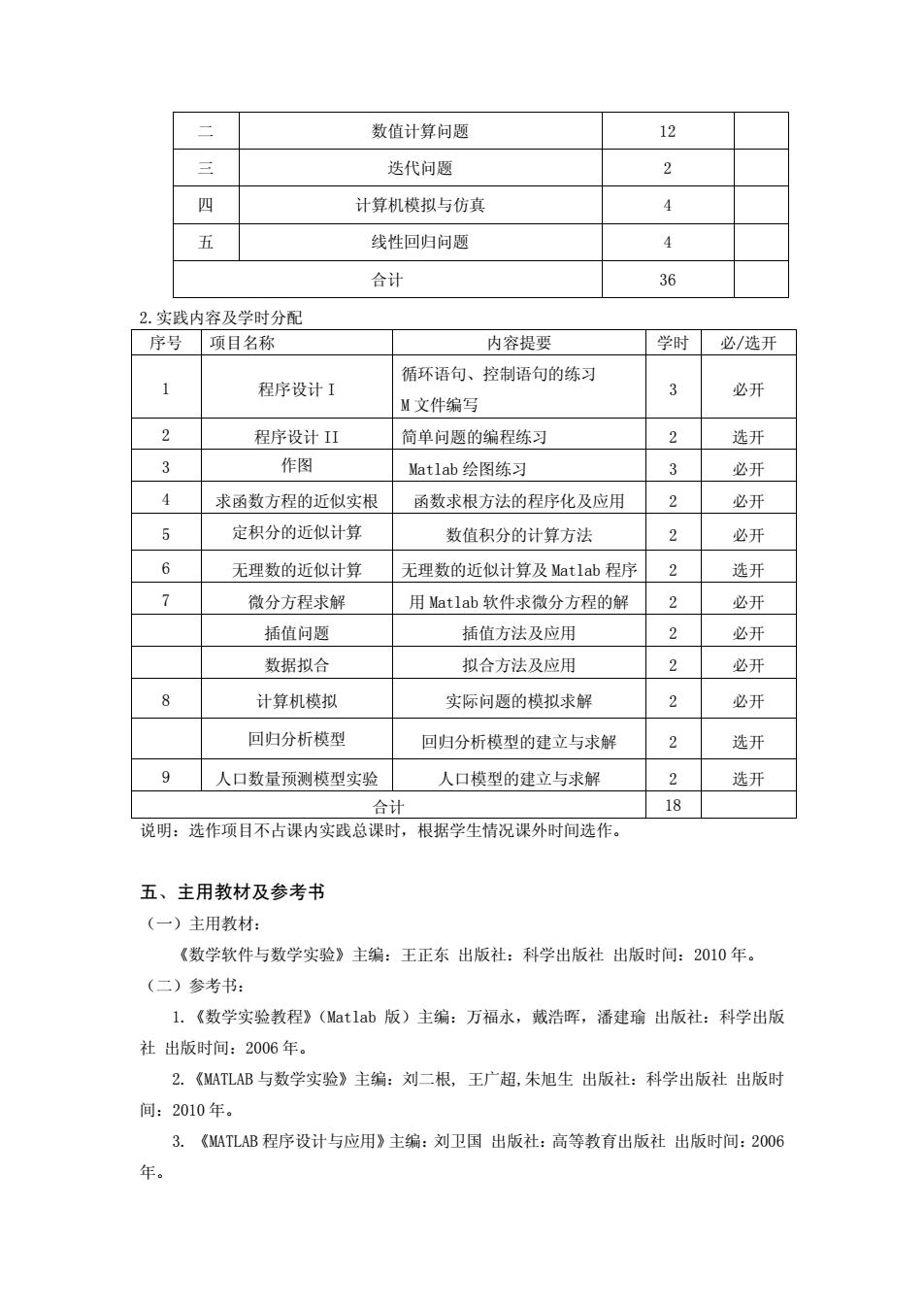
数值计算问题 12 三 迭代问题 2 四 计算机模拟与仿真 4 五 线性回归问题 4 合计 36 2.实践内容及学时分面 序号项目名称 内容提要 学时必/选开 循环语句、控制语句的练习 程序设计1 3 必开 M文件编写 2 程序设计 简单问题的编程练习 2 选开 3 作图 Matlab绘图练习 3 必开 求函数方程的近似实根 函数求根方法的程序化及应用 2 必开 定积分的近似计算 数值积分的计算方法 2 必开 无理数的近似计算 无理数的近似计算及Matlab程序 2 选开 微分方程求解 用Matlab软件求微分方程的解 2 必开 插值问题 插值方法及应用 2必开 数据拟合 拟合方法及应用 2 必开 计算机模拟 实际问题的模拟求解 2 必开 回归分析模型 回归分析模型的建立与求解 2 选开 9人口数最预测模型实验 人口模型的建立与求解 2选开 合d 18 说明:选作项目不占课内实践总课时,根据学生情况课外时间选作。 五、主用教材及参考书 (一)主用教材: 《数学软件与数学实验》主编:王正东出版社:科学出版社出版时间:2010年。 (二)参考书: 1.《数学实验教程》(Matlab版)主编:万福永,戴浩晖,潘建瑜出版社:科学出版 社出版时间:2006年。 2.《ATLB与数学实验》主编:刘二根,王广超,朱旭生出版社:科学出版社出版时 间:2010年。 3.《MATLAB程序设计与应用》主编:刘卫国出版社:高等教有出版社出版时间:2006 年
二 数值计算问题 12 三 迭代问题 2 四 计算机模拟与仿真 4 五 线性回归问题 4 合计 36 2.实践内容及学时分配 序号 项目名称 内容提要 学时 必/选开 1 程序设计 I 循环语句、控制语句的练习 M 文件编写 3 必开 2 程序设计 II 简单问题的编程练习 2 选开 3 作图 Matlab 绘图练习 3 必开 4 求函数方程的近似实根 函数求根方法的程序化及应用 2 必开 5 定积分的近似计算 数值积分的计算方法 2 必开 6 无理数的近似计算 无理数的近似计算及 Matlab 程序 2 选开 7 微分方程求解 用 Matlab 软件求微分方程的解 2 必开 插值问题 插值方法及应用 2 必开 数据拟合 拟合方法及应用 2 必开 8 计算机模拟 实际问题的模拟求解 2 必开 回归分析模型 回归分析模型的建立与求解 2 选开 9 人口数量预测模型实验 人口模型的建立与求解 2 选开 合计 18 说明:选作项目不占课内实践总课时,根据学生情况课外时间选作。 五、主用教材及参考书 (一)主用教材: 《数学软件与数学实验》主编:王正东 出版社:科学出版社 出版时间:2010 年。 (二)参考书: 1.《数学实验教程》(Matlab 版)主编:万福永,戴浩晖,潘建瑜 出版社:科学出版 社 出版时间:2006 年。 2.《MATLAB 与数学实验》主编:刘二根, 王广超,朱旭生 出版社:科学出版社 出版时 间:2010 年。 3. 《MATLAB 程序设计与应用》主编:刘卫国 出版社:高等教育出版社 出版时间:2006 年

执笔:赵国喜 审定:朱耀生梁桂珍
执笔:赵国喜 审定:朱耀生 梁桂珍