
《数学建模》教学大纲 课程编码:110892 课程名称:数学建模 学时/学分:54/3 先修课程:《数学分析》、《高等代数》、《数学软件与实验》、《概率论与数理统计》、《常 微分方程》 适用专业:数学与应用数学 开课教研室:应用数学教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的专业基础课。 2.课程任务:本课程是研究如何将数学方法和计算机知识结合起来用于解决实际问题 的一门交叉学科,是集经典数学、现代数学和实际问题为一体的一门新型课程,是应用数学 解决实际问题的重要手段和途径。通过数学建模有关的概念、特征的学习和数学建模实例的 介绍,使学生较为系统地学握利用数学工具建立数学模型的基本步骤、基本技能与常见方法, 培养学生双向翻译能力,数学推导计算和简化分析能力和用数学方法和思想分析、解决实际 问题的初步能力。 二、课程教学基本要求 《数学建模》是一门应用性较强的新兴课程,主要培养学生应用数学理论和数学思想方 法,利用计算机技术等辅助手段,分析、解决实际问题的综合能力。由于该课程的性质、特 点、内容不同于其它课程,教学形式应该是讲授与个人作业相结合,教学方法则是以启发式 教学为主,学生动手实践为辅的双向教学模式。 本课程开设在第5学期,共54学时,其中课堂讲授36学时,课内实践18学时。 成绩考核形式:末考成绩(开卷考试)(70%)+平时成绩(平时测验、作业、课堂提问 课堂讨论等)(30%)。成绩评定采用百分制,60分为及格。 三、课程教学内容 第一章数学建模概论 1.教学基本要求 让学生了解数学建模相关基本概念,了解课程特点,为后继学习莫定基础, 2.要求学生掌握的基本概念、理论、技能 通过本章教学使学生了解数学模型、数学建模的概念,了解数学模型的特点和分类,初 步掌握数学建模的基本方法和步骤,培养学生把实际问题翻译成数学问题的能力
《数学建模》教学大纲 课程编码:110892 课程名称:数学建模 学时/学分:54/3 先修课程:《数学分析》、《高等代数》、《数学软件与实验》、《概率论与数理统计》、《常 微分方程》 适用专业:数学与应用数学 开课教研室:应用数学教研室 一、课程性质与任务 1.课程性质:本课程是数学与应用数学专业的专业基础课。 2.课程任务:本课程是研究如何将数学方法和计算机知识结合起来用于解决实际问题 的一门交叉学科,是集经典数学、现代数学和实际问题为一体的一门新型课程,是应用数学 解决实际问题的重要手段和途径。通过数学建模有关的概念、特征的学习和数学建模实例的 介绍,使学生较为系统地掌握利用数学工具建立数学模型的基本步骤、基本技能与常见方法, 培养学生双向翻译能力,数学推导计算和简化分析能力和用数学方法和思想分析、解决实际 问题的初步能力。 二、课程教学基本要求 《数学建模》是一门应用性较强的新兴课程,主要培养学生应用数学理论和数学思想方 法,利用计算机技术等辅助手段,分析、解决实际问题的综合能力。由于该课程的性质、特 点、内容不同于其它课程,教学形式应该是讲授与个人作业相结合,教学方法则是以启发式 教学为主,学生动手实践为辅的双向教学模式。 本课程开设在第 5 学期,共 54 学时,其中课堂讲授 36 学时,课内实践 18 学时。 成绩考核形式:末考成绩(开卷考试)(70%)+平时成绩(平时测验、作业、课堂提问、 课堂讨论等)(30%)。成绩评定采用百分制,60 分为及格。 三、课程教学内容 第一章 数学建模概论 1.教学基本要求 让学生了解数学建模相关基本概念,了解课程特点,为后继学习奠定基础。 2.要求学生掌握的基本概念、理论、技能 通过本章教学使学生了解数学模型、数学建模的概念,了解数学模型的特点和分类,初 步掌握数学建模的基本方法和步骤,培养学生把实际问题翻译成数学问题的能力

3.教学重点和难点 教学重点是数学建模的基本步骤, 教学难点是如何把实际问题翻译成数学问题。 4.教学内容 第一节从现实对象到数学模型 第二节数学建模的重要意义 第三节建模示例之一椅子能在不平的地面上放稳吗 第四节建模示例之二商人们怎样安全过河 第五节建模示例之三何预报人口的增长 第六节数学建模的基本方法和步强 第七节数学模型的特点和分类 第八节数学建模能力的培养 第二章初等建模 1.教学基本要求 让学生进一步掌握用数学知识分析、解决实际问题的方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生掌握比例方法、类比方法、图解法、定性分析方法等建模方法, 能够用比例分析法等方法建立数学模型,对所研究问题进行定性或定量分析。 3.教学重点和难点 重点:比例分析法、图解法等初等建模方法。 难点:初等模型的建立无差别曲线的概念与应用。 4.教学内容 第一节公平的席位分配 *第二节录像机计数器的用途 第三节双层玻璃窗的功效 第四节汽车刹车距离 第五节划艇比赛的成绩 第六节动物的身长和体重 第七节实物交换 第八节核军备竞赛 *第九节扬帆远航 第十节量纲分析与无量纲化
3.教学重点和难点 教学重点是数学建模的基本步骤。 教学难点是如何把实际问题翻译成数学问题。 4.教学内容 第一节 从现实对象到数学模型 第二节 数学建模的重要意义 第三节 建模示例之一 椅子能在不平的地面上放稳吗 第四节 建模示例之二 商人们怎样安全过河 第五节 建模示例之三何预报人口的增长 第六节 数学建模的基本方法和步骤 第七节 数学模型的特点和分类 第八节 数学建模能力的培养 第二章 初等建模 1.教学基本要求 让学生进一步掌握用数学知识分析、解决实际问题的方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生掌握比例方法、类比方法、图解法、定性分析方法等建模方法, 能够用比例分析法等方法建立数学模型,对所研究问题进行定性或定量分析。 3.教学重点和难点 重点:比例分析法、图解法等初等建模方法。 难点:初等模型的建立;无差别曲线的概念与应用。 4.教学内容 第一节 公平的席位分配 *第二节 录像机计数器的用途 第三节 双层玻璃窗的功效 第四节 汽车刹车距离 第五节 划艇比赛的成绩 第六节 动物的身长和体重 第七节 实物交换 *第八节 核军备竞赛 *第九节 扬帆远航 第十节 量纲分析与无量纲化

第三章 简单的优化模型 1.教学基本要求 让学生掌握用极值理论等常见数学知识建立数学模型的方法 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够用函数极值理论等常见数学知识建立数学模型,对所研究 问题进行定性或定量分析。 3.教学重点和难点 重点:微积分模型的建立:存贮模型的建立与应用。 难点:效用最大化模型的建立与应用。 4.教学内容 第一节存贮模型 第二节生猪的出售时机 第三节森林救火 第四节消费者的洗择 第五节生产者的决策 幸第六节血管分支 第七节冰山运输 第四章 数学规划模型 1.教学基本要求 掌握常见数学规划模型和软件求解方法:能够用数学规划知识对实际问题建立模型,并 进行分析:了解多目标规划的求解方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生掌握线性规划、整数规划、01规划、非线性规划等常见规划 模型基本知识和用数学软件求解规划问题的方法,并能运用相关知识对实际问题建立模型, 对结果进行分析。 3.教学重点和难点 重点:线性规划、整数规划、0-1规划,Lingo软件编程。 难点:对实际问题,如何建立规划模型:Lig0集合语言。 4.教学内容 第一节奶制品的生产与销售 第二节自来水输送与货机装运 第三节汽车生产与原油采购 第四节接力队的选拔与选课策照
第三章 简单的优化模型 1.教学基本要求 让学生掌握用极值理论等常见数学知识建立数学模型的方法 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够用函数极值理论等常见数学知识建立数学模型,对所研究 问题进行定性或定量分析。 3.教学重点和难点 重点:微积分模型的建立;存贮模型的建立与应用。 难点:效用最大化模型的建立与应用。 4.教学内容 第一节 存贮模型 第二节 生猪的出售时机 第三节 森林救火 第四节 消费者的选择 第五节 生产者的决策 *第六节 血管分支 第七节 冰山运输 第四章 数学规划模型 1.教学基本要求 掌握常见数学规划模型和软件求解方法;能够用数学规划知识对实际问题建立模型,并 进行分析;了解多目标规划的求解方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生掌握线性规划、整数规划、0-1 规划、非线性规划等常见规划 模型基本知识和用数学软件求解规划问题的方法,并能运用相关知识对实际问题建立模型, 对结果进行分析。 3.教学重点和难点 重点:线性规划、整数规划、0-1 规划,Lingo 软件编程。 难点:对实际问题,如何建立规划模型;Lingo 集合语言。 4.教学内容 第一节 奶制品的生产与销售 第二节 自来水输送与货机装运 第三节 汽车生产与原油采购 第四节 接力队的选拔与选课策略

第五节饮料厂的生产与检修 第六节钢管和易拉罐下料 第五章 微分方程模型 1.教学基本要求 掌握用微分方程知识建立数学模型的基本方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够对实际问题借助于常微分方程知识建立数学模型,通过方 程的解析解,给出相关结论或解释 3.教学重点和难点 重点:如何对实际问题建立微分方程模型传染病模型的四种情况的建模,求解与它们 的一些应用。 难点:微分方程模型的建立。 4.教学内容 第一节传染病模型 第二节经济增长模型 *第三节正规战与游击战 第四节药物在体内的分布与排除 *第五节香烟过滤嘴的作用 第六节人口的预测和控制 *第七节烟雾的扩散与消失 *第八节万有引力定律的发现 第六章 稳定性模型 1.教学基本要求 了解微分方程稳定性理论,掌握用稳定性分析研究实际问题的方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够对实际问题建立微分方程模型,并结合稳定性分析的知识 分析、解释实际问题。 3.教学重点和难点 重点:微分方程模型的建立,稳定性分析。 难点:稳定性分析。 4.教学内容 第一节捕鱼业的持续收获
第五节 饮料厂的生产与检修 第六节 钢管和易拉罐下料 第五章 微分方程模型 1.教学基本要求 掌握用微分方程知识建立数学模型的基本方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够对实际问题借助于常微分方程知识建立数学模型,通过方 程的解析解,给出相关结论或解释。 3.教学重点和难点 重点:如何对实际问题建立微分方程模型;传染病模型的四种情况的建模,求解与它们 的一些应用。 难点:微分方程模型的建立。 4.教学内容 第一节 传染病模型 第二节 经济增长模型 *第三节 正规战与游击战 第四节 药物在体内的分布与排除 *第五节 香烟过滤嘴的作用 第六节 人口的预测和控制 *第七节 烟雾的扩散与消失 *第八节 万有引力定律的发现 第六章 稳定性模型 1.教学基本要求 了解微分方程稳定性理论,掌握用稳定性分析研究实际问题的方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够对实际问题建立微分方程模型,并结合稳定性分析的知识 分析、解释实际问题。 3.教学重点和难点 重点:微分方程模型的建立,稳定性分析。 难点:稳定性分析。 4.教学内容 第一节 捕鱼业的持续收获

*第二节军备竞赛 第三节种群的相互竞争 第四节种群的相互依存 第五节食饵捕食者模因 *第六节微分方程稳定性理论简介 第七章 差分方程模型 1.教学基本要求 掌握用差分方程知识建立数学模型的基本方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够对实际问题借助于差分方程知识建立数学模型,并对问题 进行分析或解释。 3.教学重点和难点 重点:差分方程的解法和建模方法 难点:差分方程模型的建立。 4.教学内容 第一节市场经济中的蛛网模型 第二节减肥计划一节食与运动 *第三节差分形式的阻滞增长模型 第四节差分形式的阻滞增长模型 ◆第五节差分方程简介 第八章离散模型 1.教学基本要求 了解图论、网络流等建模方法,掌握层次分析法。 2要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生掌据层次分析法相关知识,并能用层次分析法建立模型,解决 实际问题。 3.教学重点和难点 重点:层次分析法建模。 难点:层次分析法基本理论。 4.教学内容 第一节层次分析模型 第二节循环比赛的名次
*第二节 军备竞赛 第三节 种群的相互竞争 第四节 种群的相互依存 第五节 食饵-捕食者模型 *第六节 微分方程稳定性理论简介 第七章 差分方程模型 1.教学基本要求 掌握用差分方程知识建立数学模型的基本方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够对实际问题借助于差分方程知识建立数学模型,并对问题 进行分析或解释。 3.教学重点和难点 重点:差分方程的解法和建模方法。 难点:差分方程模型的建立。 4.教学内容 第一节 市场经济中的蛛网模型 *第二节 减肥计划——节食与运动 *第三节 差分形式的阻滞增长模型 第四节 差分形式的阻滞增长模型 *第五节 差分方程简介 第八章 离散模型 1.教学基本要求 了解图论、网络流等建模方法,掌握层次分析法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生掌握层次分析法相关知识,并能用层次分析法建立模型,解决 实际问题。 3.教学重点和难点 重点:层次分析法建模。 难点:层次分析法基本理论。 4.教学内容 第一节 层次分析模型 第二节 循环比赛的名次

◆第三节社会经济系统的冲量过程 第四节效益的合理分配 ◆第五节存在公正的选举规则吗 第九章 概率模型 1.教学基本要求 掌握用概率论知识建立数学模型的基本方法。 2要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够用概率论知识对实际问题建立模型,并给出相关结论或解 释。 3.教学重点和难点 重点:概率模型的建立。 难点:概率模型的建立。 4.教学内容 第一节传送系统的效率 第二节报童的诀窍 第三节随机存贮策略 ◆第四节轧钢中的浪费 第五节随机人口模型r *第六节航空公司的预订票策略 *第七节广告中的学问 第十章 统计回归模型 1.教学基本要求 掌握用数理统计和回归分析知识建立数学模型的基本方法,并能够借助于数学软件对模 型求解。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够用数理统计和回归分析知识对实际问题建立模型,并给出 相关结论或解释。 3.教学重点和难点 重点:统计回归模型的建立和求解 难点:统计回归模型的改进。 4.教学内容 第一节牙音的销售量
*第三节 社会经济系统的冲量过程 第四节效益的合理分配 *第五节 存在公正的选举规则吗 第九章 概率模型 1.教学基本要求 掌握用概率论知识建立数学模型的基本方法。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够用概率论知识对实际问题建立模型,并给出相关结论或解 释。 3.教学重点和难点 重点:概率模型的建立。 难点:概率模型的建立。 4.教学内容 第一节 传送系统的效率 第二节 报童的诀窍 第三节 随机存贮策略 *第四节 轧钢中的浪费 第五节 随机人口模型 r *第六节 航空公司的预订票策略 *第七节 广告中的学问 第十章 统计回归模型 1.教学基本要求 掌握用数理统计和回归分析知识建立数学模型的基本方法,并能够借助于数学软件对模 型求解。 2.要求学生掌握的基本概念、理论、技能 通过本章学习,要求学生能够用数理统计和回归分析知识对实际问题建立模型,并给出 相关结论或解释。 3.教学重点和难点 重点:统计回归模型的建立和求解。 难点:统计回归模型的改进。 4.教学内容 第一节 牙膏的销售量
第二节软件开发人员的薪金 第三节酶促反应 +第四节投资额与生产总值和物价指数 第五节教学评估 说明:以上各部分教学内容中,带“幸”的部分是选讲内容,以学生课外自学为主。 四、学时分配 1.讲授内容及学时分配 章序 内容 课时 备注 建立数学模型 2 初等模型 6 简单的优化模型 3 数学规划模型 6 五 微分方程模型 3 六 稳定性模型 3 七 差分方程模型 2 八 离散模型 5 九 概率模型 3 统计回归模型 3 合计 36 2实践内容及学时分配 序号 项目 内容提要 学时 必/选开 名称 1 初等方法建模 练习数学建模的基本步骤 3 必开 2 规划方法建模 练习规划模型的建立和求解方法 必开 3 微分方程建模 练习用微分方程知识建模方法 3 必开 4 层次分析法建模练习稳定性理论建模的方法 选开 5 稳定性理论建模练习用概率论知识建立模型的方法 3 必开 6 概率方法建模 练习用回归分析知识建立模型的方法 必开 7 统计回归方法建模练习用量纲分析法建模的方法 3 必开 8 综合性实验 练习用层次分析法建模的方法 选开 合计 18
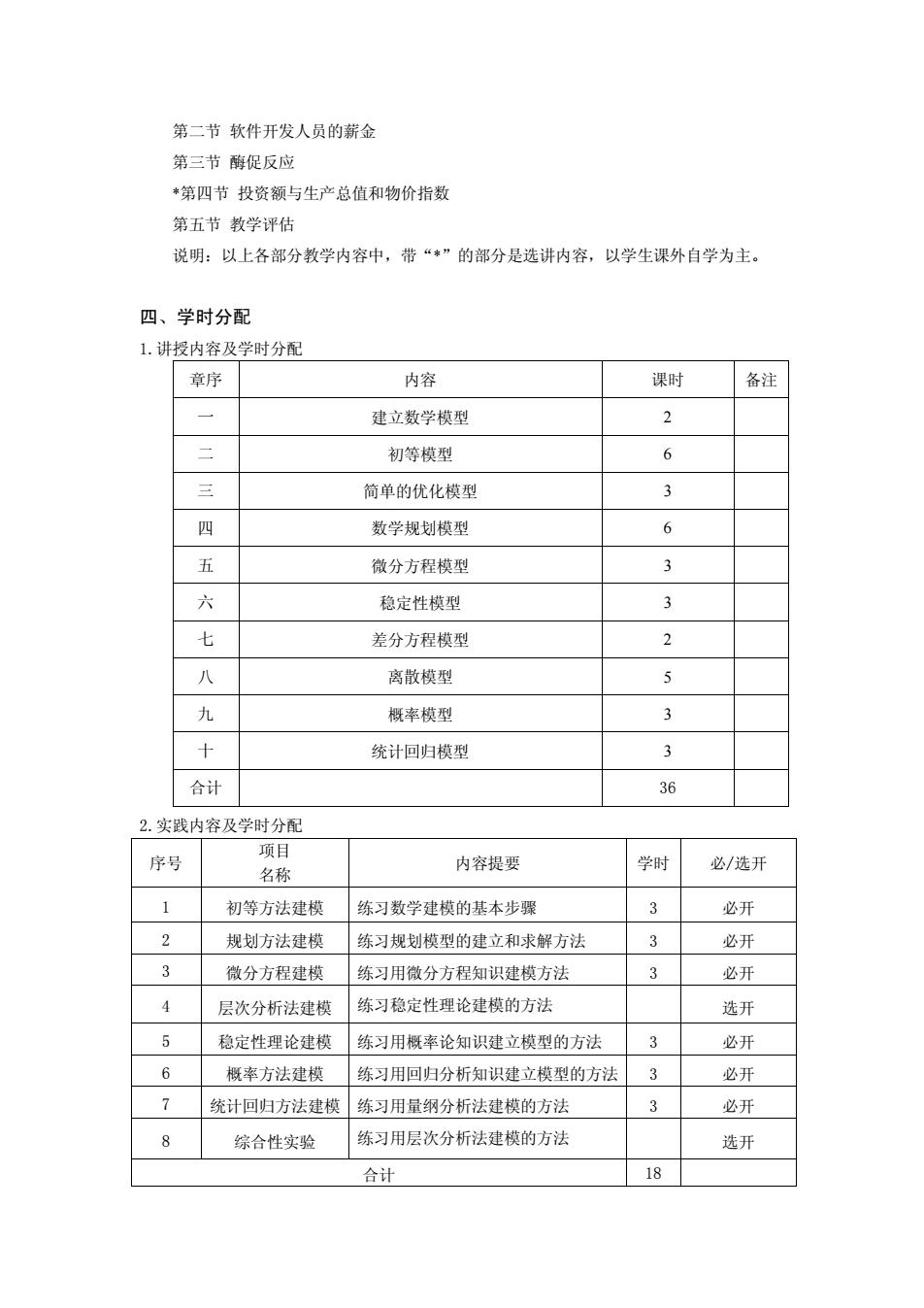
第二节 软件开发人员的薪金 第三节 酶促反应 *第四节 投资额与生产总值和物价指数 第五节 教学评估 说明:以上各部分教学内容中,带“*”的部分是选讲内容,以学生课外自学为主。 四、学时分配 1.讲授内容及学时分配 章序 内容 课时 备注 一 建立数学模型 2 二 初等模型 6 三 简单的优化模型 3 四 数学规划模型 6 五 微分方程模型 3 六 稳定性模型 3 七 差分方程模型 2 八 离散模型 5 九 概率模型 3 十 统计回归模型 3 合计 36 2.实践内容及学时分配 序号 项目 名称 内容提要 学时 必/选开 1 初等方法建模 练习数学建模的基本步骤 3 必开 2 规划方法建模 练习规划模型的建立和求解方法 3 必开 3 微分方程建模 练习用微分方程知识建模方法 3 必开 4 层次分析法建模 练习稳定性理论建模的方法 选开 5 稳定性理论建模 练习用概率论知识建立模型的方法 3 必开 6 概率方法建模 练习用回归分析知识建立模型的方法 3 必开 7 统计回归方法建模 练习用量纲分析法建模的方法 3 必开 8 综合性实验 练习用层次分析法建模的方法 选开 合计 18

说明:选开内容根据学生实际情况在课外实践进行,不占课内实践课时。 五、主用教材及参考书 (一)主用教材: 《数学模型》主编:姜启源谢金星叶俊出版社:高等教有出版社出版时间:2008 年。 (二)参考书: 1.《数学建模与实验》主编:陈恩水,王峰出版社:科学出版社出版时间:2008年。 2.《数学建模》主编:陈东意,李冬梅,王树忠出版社:科学出版社出版时间:2007 年。 3.《数学建模方法及其应用》主编:韩中庚出版社:高等教有出版社出版时间:2009 年。 执笔:赵国喜 审定:朱耀生梁桂珍
说明:选开内容根据学生实际情况在课外实践进行,不占课内实践课时。 五、主用教材及参考书 (一)主用教材: 《数学模型》主编:姜启源 谢金星 叶俊 出版社:高等教育出版社 出版时间:2008 年。 (二)参考书: 1.《数学建模与实验》主编:陈恩水,王峰 出版社:科学出版社 出版时间:2008 年。 2.《数学建模》主编:陈东彦, 李冬梅, 王树忠 出版社:科学出版社 出版时间:2007 年。 3.《数学建模方法及其应用》主编:韩中庚 出版社:高等教育出版社 出版时间:2009 年。 执笔:赵国喜 审定:朱耀生 梁桂珍